k — волновой вектор; k
1.15.4. Волновое уравнение
Продифференцируем дважды уравнение плоской бегущей волны (17.2) по x, затем по t:
ξ |
|
1 |
|
|
ξ |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
x |
|
v |
f , |
x |
2 |
|
v |
2 |
f ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
сравнивая вторые производные по x и t, получим дифференциальное уравнение второго порядка в частных производных
|
|
ξ |
|
1 ξ |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
x |
2 |
|
2 |
t |
2 |
|
|
(17.4) |
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
— волновое уравнение. |
|
|
|
|
|
|
|
|
|
|
Общее решение волнового уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
f2 |
|
x |
|
|
ξ x,t f1 t |
v |
|
t |
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
прямая волна |
|
|
|
обратная волна |
Вид функций f1 и f2 определяется начальными условиями.
141
II семестр
Лекция 18
3. Электродинамика
3.1. Электромагнитное поле
3.1.1. Поле
Поле — любая изменяющаяся в пространстве физическая величина.
|
Поле |
|
|
скалярное |
векторное |
|
температурное поле T(x, y, z) |
гравитационное поле |
|
изображается изолиниями |
изображается силовыми линиями |
|
(поверхностями постоянной величины) |
|
|
Силовые линии строят так, чтобы их густота была пропорциональна модулю векторного поля.
3.1.2. Электрический заряд. Закон сохранения электрического заряда
Электрический заряд — квантовое число, характеризующее частицу как источник электромагнитного взаимодействия (см. 0.3 и 7.4.2).
В классической физике электрический заряд — скалярная алгебраическая величина — характеристика электрически заряженного тела, т. е. тела, на которое действует электромагнитное поле (см. 3.1.3);
[q] = Кл (кулон).
Также электрическим зарядом часто называют саму заряженную частицу (тело).
Элементарный заряд — минимальный (по модулю) электрический заряд частиц, наблюдаемых в свободном состоянии46;
e = 1,60·10–19 Кл.
Электрически изолированная система — система тел, для которой сумма элек-
трических зарядов частиц, появившихся в этой системе, равна нулю.
Закон сохранения электрического заряда: суммарный электрический заряд лю-
бой электрически изолированной системы не изменяется в любых процессах, происходящих в этой системе:
Q const .
Линейная плотность электрического заряда — заряд, приходящийся на еди-
ничный участок протяжённого заряженного тела:
46 Кварки, электрический заряд которых по модулю равен 13e и 32e (см. 7.5.1), в свободном состоя-
нии не наблюдаются.
142
Поверхностная плотность электрического заряда — заряд, приходящийся на единичный участок поверхности заряженного тела:
Объёмная плотность электрического заряда — заряд, приходящийся на уча-
сток заряженного тела единичного объёма:
Электрический заряд тела выражается через плотности заряда следующим образом:
q τdl σdS ρdV ,
здесь l, S, V — соответственно длина, площадь поверхности и объём заряженного тела.
Электрический ток — упорядоченное движение электрически заряженных частиц.
3.1.3. Электромагнитное поле
Электромагнитное поле — физический объект — действует на электрически заряженные частицы.
Для того чтобы характеризовать электромагнитное поле в какой-либо точке пространства, мысленно вносим в эту точку пробный заряд.
Пробный заряд — материальная точка, имеющая положительный электрический заряд, настолько малый, чтобы не искажать электромагнитное поле, т. е. не изменять расположение заряженных тел, создающих это поле.
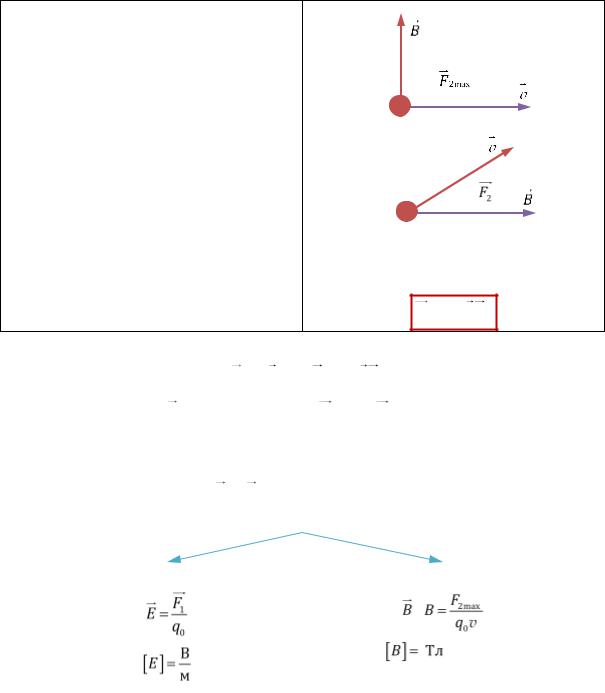
На частицу с зарядом q0 (пробным зарядом), движущуюся со скоростью v , электромагнитное поле действует с силой
F F1 q0 , поле F2 q0 ,v, поле .
Здесь F1 — составляющая силы, которая не зависит от скорости пробного заряда, а F2 зависит в т. ч. от скорости пробного заряда.
Попробуем ввести характеристики, которые определяли бы поле и не зависели бы от свойств заряженного тела, помещённого в это поле. Для этого рассмотрим две
ситуации, в одной из которых F2 0, а в другой F1 0 (ТАБЛ. 18.1).
Все заряды неподвижны:
2 |
|
1 |
0 |
|
|
F |
0 |
, F F |
q , поле |
|
. |
Создадим такие условия, при которых поле действует только на движущийся заряд:
F1 0 |
, F F2 q0 ,v, поле . |
|
|
|
Из опыта: |
|
|
|
|
|
1) F2 |
~ q0; |
|
|
|
|
|
2) F2 |
~ v; |
|
|
Рассмотрим отношение F1 |
q0 |
. Оно опре- |
3) F2 зависит от направления |
v |
и изме- |
няется от 0 до Fmax; |
|
|
деляется только величиной поля и явля- 4) F2 ~ полю.
ется одной из характеристик поля: Отношение модуля максимальной силы, с которой поле действует на пробный заряд, к величине этого заряда и модулю его скорости — характеристика только поля:
|
|
|
|
F |
|
|
|
B |
F |
|
|
|
|
E |
1 |
|
|
|
2max |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
q v |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
B — индукция магнитного поля (маг- |
|
— напряжённость электрического |
нитная компонента электромагнитного |
|
поля (электрическая компонента элек- |
поля). |
|
|
|
|
тромагнитного поля). |
Направление B совпадает с ориента- |
|
цией магнитной стрелки, помещённой в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данную точку пространства: |
|
|
|
|
|
|
|
S |
|
|
N |
|
Демонстрации: 1) Султаны |
Демонстрации: |
1) Опыт Эрстеда |
|
|
|
2) Силовые линии |
|
|
|
|
|
2) Силовые линии |
|
|
|
электрического |
|
|
|
|
|
|
|
магнитного поля |
|
|
|
поля47 |
|
|
|
|
|
|
|
|
|
|
|
Сила, с которой электромагнитное поле |
Обратная задача: найти F2 . |
|
|
|
|
|
|
|
действует на неподвижный пробный за- |
Зная B , можно найти силу, с которой |
|
ряд |
|
|
|
электромагнитное |
|
поле действует на |
|
|
|
|
|
|
|
движущийся пробный заряд. Оказыва- |
|
|
F1 q0 E |
. |
|
|
ется, что F2 v , F2 |
B . |
|
|
|
|
|
|
|
|
|
47 Демонстрации «Силовые линии электрического поля» и «Силовые линии магнитного поля» рекомендуется показывать последовательно одну за другой.
q0 +
q0 + α 
3.1.4. Силовые характеристики электромагнитного поля
Для того чтобы охарактеризовать электромагнитное поле как единый объект, нужно ввести два вектора — E и B .
Основные силовые характеристики электромагнитного поля
Напряжённость электрического поля |
Индукция магнитного поля |
|
, |
|
(тесла) |
145
Вспомогательные силовые характеристики электромагнитного поля
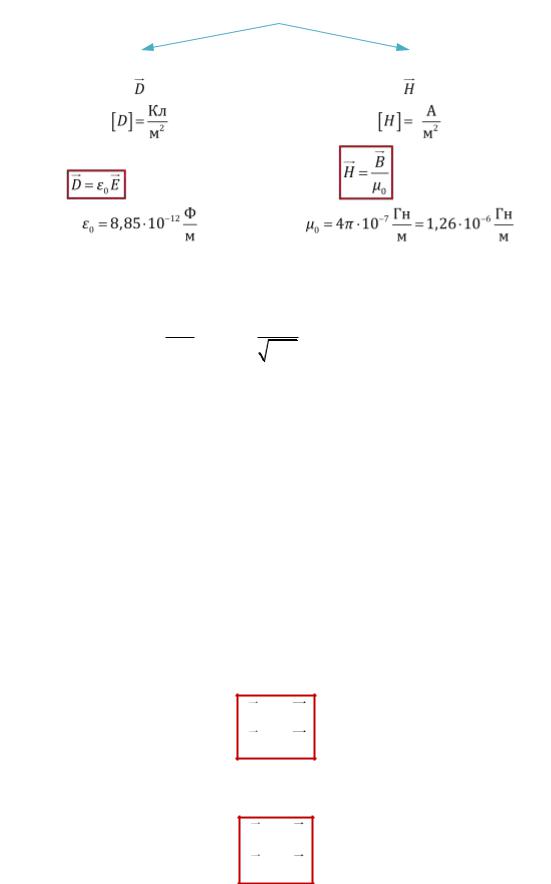
Электрическое смещение |
Напряжённость магнитного поля |
(в вакууме)
(в вакууме)
— электрическая постоянная |
— магнитная постоянная |
Электрическая и магнитная постоянные не имеют физического смысла, они — константы СИ. Физический смысл имеет величина
1 |
|
c |
2 |
, c |
1 |
3,00 |
8 м |
ε μ |
|
|
10 |
с |
|
|
|
ε μ |
|
0 |
0 |
|
|
|
0 |
0 |
|
|
— скорость электромагнитных волн в вакууме.
Вспомогательные силовые характеристики нужны для описания электромагнитного поля в веществе (см. 3.3.3 и 3.11.2).
3.1.5. Принцип суперпозиции полей
Этот принцип следует из опыта.
Принцип суперпозиции полей:
напряжённость электрического
индукция магнитного поля
заряженных частиц
движущихся заряженных частиц
полей, создаваемых каждым из этих
Для дискретного распределения
зарядов
токов
E Ei ,
B Bi .
Для непрерывного распределения
зарядов
токов
E dE,
B dB.
146
3.1.6. Уравнения Максвелла
Уравнения Максвелла — основные уравнения классической электродинамики — постулируются. Они — обобщение опытных фактов — законов электродинамики. Мы рассмотрим каждый из этих законов в дальнейшем.
Уравнения Максвелла в интегральной форме 48
Edl |
B |
dS |
|
t |
|
S |
|
|
|
|
|
|
|
D |
Hdl j |
t |
dS |
S |
|
|
|
|
DdS ρdV |
|
V |
|
|
|
BdS 0 |
|
|
|
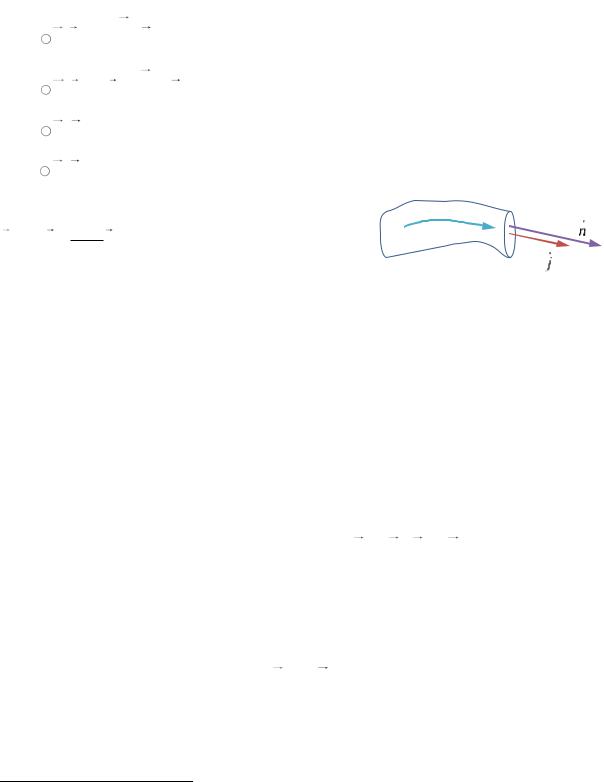
Здесь ρ — объёмная плотность заряда;
|
j |
dI |
n |
dq |
n |
— |
плотность |
тока |
|
dS |
dtdS |
|
|
|
|
|
|
|
(см. РИС. 18.1) (I — сила тока, dS — элементарная площадка, перпендикулярная направлению движения зарядов, t — время).
Имеются в виду свободные заряды — заряды, нарушающие электронейтральность вещества, и макротоки — упорядоченное движение заряженных частиц, при котором они перемещаются на расстояния, много большие межмолекулярных расстояний.
Вуравнениях I, II L — произвольная замкнутая кривая, S — произвольная поверхность, ограниченная этой кривой.
Вуравнениях III, IV S — произвольная замкнутая поверхность, V — объём, ограниченный этой поверхностью.
3.1.7. Материальные уравнения
Материальные уравнения — уравнения, связывающие основные и вспомогатель-
ные характеристики электромагнитного поля: E и D , B и природы вещества, в котором существует электромагнитное
H . Их вид зависит от поле.
Вещество состоит из молекул, в которых заряженные частицы (связанные заряды) движутся друг относительно друга (микротоки) и создают собственное электромагнитное поле, которое накладывается на поле свободных зарядов и макротоков.
Для изотропных диэлектриков, несегнетоэлектриков49
где ε — относительная диэлектрическая проницаемость вещества. В вакууме ε = 1.
Для изотропных магнетиков, неферромагнетиков
48Более подробно об уравнениях Максвелла — в ПАРАГРАФЕ 3.12. Элементы векторного анализа, использующиеся в уравнениях Максвелла, рассмотрим в течение семестра.
49Сведения о сегнетоэлектриках см., например, в книге [3].
где µ — относительная магнитная проницаемость вещества. В вакууме µ = 1.
3.2. Постоянное электрическое поле в вакууме
3.2.1. Электростатическое поле в вакууме
|
В этом случае |
B 0 |
, |
E |
0 |
|
t |
|
|
|
|
|
|
|
|
|
Уравнения Максвелла: |
|
|
I. |
Edl 0 |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
EdS |
Q |
|
|
|
|
|
III. |
|
S |
ρdV QS |
|
|
|
|
ε |
|
|
S |
|
V |
|
|
|
|
|
|
0 |
|
|
148
Лекция 19
3.2.2. Закон Кулона. Расчёт напряжённости электрического поля методом суперпозиции
Закон Кулона: сила взаимодействия двух точечных зарядов
F12 q1q2 r12
4πε0 r123
(см. РИС. 19.1; на этом рисунке заряды q1 и q2 одного знака).
Напряжённость электрического поля точечного заряда
Силовые линии электрического поля точечного заряда представлены на РИС. 19.2.
Любую систему заряженных тел можно разбить на точечные заряды (или заряды другой формы, поле которых легко рассчитать) и затем просуммировать (проинтегрировать) напряжённости полей этих зарядов.
ПРИМЕРЫ
1) Электрическое поле равномерно заряженного тонкого кольца
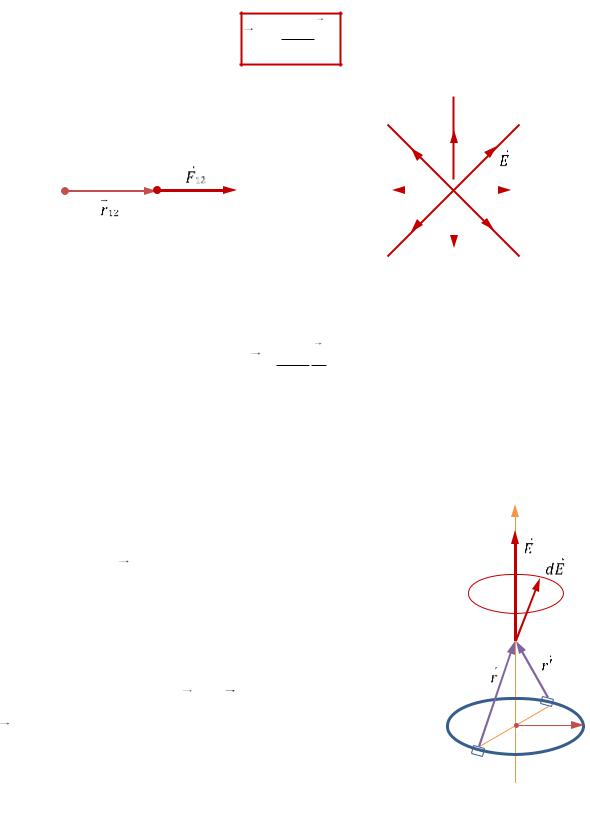
По тонкому кольцу равномерно распределён заряд Q > 0 (РИС. 19.3). Найти E z (z — ось кольца).
Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на РИС. 19.3 показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей
E dE ,
dE — напряжённость электрического поля малого заряда dq. Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю (если одинаковы все заряды dq) и направлены так, что концы этих векторов обра-
z
 A
A
θ
Q  dq′
dq′
R
O
dq
Рис. 19.3
149
зуют конус с вершиной в точке A (на РИС. 19.3 штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются,
направлен вдоль оси z:
E Ez (при z > 0).
Вычислим Ez. Напряжённость поля точечного заряда
|
dE |
dq |
r |
; |
|
|
4πε |
r |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
dE |
dq |
|
, dEz |
|
|
dq |
2 cosθ , |
4πε r |
2 |
4πε r |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
угол θ показан на РИС. 19.3. Величины r и θ одинаковы для всех элементов dq:
|
|
r |
|
R |
2 |
z |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosθ |
z |
|
|
|
|
|
|
|
z |
|
|
|
. |
r |
|
|
|
R |
|
|
z |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим эти формулы в выражение для dEz: |
|
|
|
|
dE |
|
|
|
dq z |
|
|
|
|
|
z |
0 |
|
|
|
|
|
|
|
|
|
|
|
4πε |
|
|
R |
2 |
z |
2 |
|
3 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом выражении все величины — постоянные, кроме dq. Проинтегрируем по q:
|
Q |
dq |
z |
|
|
|
|
Qz |
|
|
|
Ez |
|
|
|
|
|
|
|
. |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
3 2 |
|
|
|
2 |
|
2 |
3 2 |
|
|
0 4πε |
|
R |
z |
|
4πε |
|
R |
z |
|
|
|
|
|
|
|
|
|
|
|
|
Предельные случаи
а) z = 0 E = 0.
б) z → ∞ E = 0.
|
в) z >> R E |
|
|
Qz |
|
|
z |
4πε z |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2) Электрическое поле равномерно заряженного тонкого прямого стержня
Тонкий стержень длиной AB = l имеет заряд Q > 0, равномерно распределённый по длине стержня. Найти напряжённость электрического поля в точке, находящейся на перпендикуляре к стержню, проходящем через его середину, на расстоянии b (точка C на РИС. 19.4).
Разобьём стержень на малые отрезки, имеющие малый заряд dq. Напряжённость поля точечного заряда
по принципу суперпозиции полей
E dE .









 A
A dq′
dq′