100
p
1
 Q1
Q1
4 2
Q2
 3
3
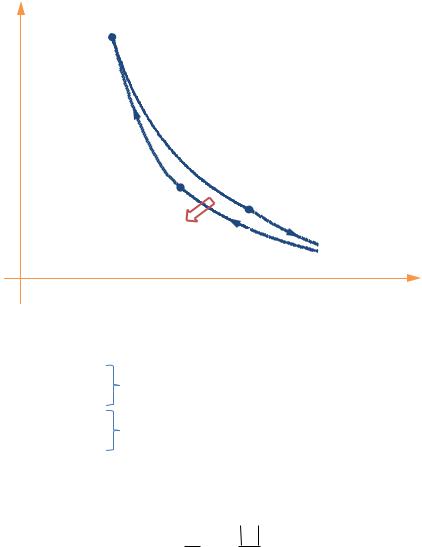
Рис. 11.8
Соответственно, цикл Карно состоит из квазистатических изотермических и адиабатных процессов (см. диаграмму РИС. 11.8):
1-2 — изотермические процессы,
3-4
2-3 — адиабатные процессы.
4-1
Найдём КПД теплового двигателя, работающего по циклу Карно. Рабочее тело — идеальный газ.
По определению
Рабочее тело сообщается с нагревателем на этапе 1-2:
|
Q1 Q12 A12 νRT1 ln |
V |
, |
|
2 |
|
|
|
|
|
V |
|
|
|
1 |
|
где T1 — температура нагревателя (см. ПРИМЕР РАСЧЁТА РАБОТЫ; по уравнению Мен- делеева-Клапейрона в процессе 1-2 pV = νRT1), V1 и V2 — соответственно объёмы газа в состояниях 1 и 2;
а с холодильником — на этапе 3-4:
Q2 Q34 A34 νRT2 lnV4 νRT2 lnV3 ,
V3 V4
где T2 — температура холодильника, V3 и V4 — соответственно объёмы газа в состояниях 3 и 4.
Найдём связь между отношениями объёмов через уравнение адиабаты в координатах (V, T):
101
|
|
|
|
|
i |
|
|
i |
|
|
i |
V T |
2 |
V T |
2 |
, |
|
|
|
|
|
|
|
VT |
|
2 |
1 |
3 |
2 |
|
2 |
const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
2 |
V T 2 . |
|
|
V T |
|
|
|
1 |
1 |
4 |
2 |
|
Разделим верхнее уравнение на нижнее:
V2 V3 .
V1 V4
Подставим эти результаты в выражение для КПД:
|
νRT ln |
V |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
V |
|
|
T |
|
T T |
|
η 1 |
1 |
|
|
|
|
4 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
νRT ln |
V |
|
|
T |
|
|
T |
|
|
2 |
|
|
1 |
|
|
1 |
|
1 |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
|
|
T T |
|
|
|
|
|
|
1 |
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
Карно |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
всегда η < 1.
2.5.4. Теоремы Карно (без доказательства)
1.КПД теплового двигателя, рабочее тело которого совершает цикл Карно, не зависит от природы рабочего тела и равен отношению максимальной и минимальной температур к максимальной температуре рабочего тела:
|
η |
|
T |
T |
|
max |
min |
|
|
|
|
Карно |
|
T |
|
|
|
|
|
|
|
max |
2.КПД любого теплового двигателя, рабочее тело которого совершает обратимый цикл, не превосходит КПД теплового двигателя, рабочее тело которого совершает цикл Карно:
3.КПД теплового двигателя, рабочее тело которого совершает необратимый цикл, меньше КПД теплового двигателя, рабочее тело которого совершает обратимый цикл, при прочих равных условиях (при тех же максимальной и минимальной температурах рабочего тела):
Из трёх теорем Карно следует, что
η |
Tmax Tmin . |
необрат |
|
Tmax |
|
|
|
2.6. Энтропия. II начало термодинамики
2.6.1. Неравенство Клаузиуса
Пусть некоторое рабочее тело совершает цикл между двумя тепловыми резервуарами с температурами T1 и T2 (T1 > T2). Из теорем Карно
η η |
T2 T1 |
|
Q1 Q2 |
T1 T2 |
1 |
Q2 |
1 T2 |
Q2 T2 |
|
|
Карно |
T1 |
|
Q1 |
T1 |
|
Q1 |
T1 |
Q1 T1 |
|
|
|
102
(так как Q2 < 0; здесь использованы обозначения ПРЕДЫДУЩЕГО ПАРАГРАФА);
|
|
|
|
Q |
|
Q |
0 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
T |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
— неравенство Клаузиуса; |
Q |
— приве- |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
дённая теплота. В этих уравнениях знак p |
Q1i |
|
«=» соответствует обратимому циклу, «<» |
|
|
|
— необратимому. |
|
|
|
|
|
|
|
|
|
Сумма приведённых теплот, полученных |
|
|
|
|
рабочим телом за цикл, равна нулю, если |
|
|
|
|
цикл обратимый, и меньше нуля, если цикл |
|
|
|
|
необратимый. |
|
|
|
|
|
|
|
ΔQ2i |
|
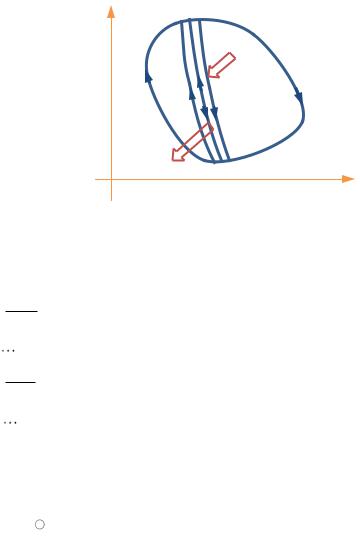
Если имеется бесконечное множество теп- |
|
|
|
|
|
|
|
ловых резервуаров, то между ними можно |
0 |
V |
|
совершить бесконечное множество обрати- |
|
|
|
|
|
мых циклов. Соответственно, любой цикл |
|
|
Рис. 11.9 |
|
можно разбить на бесконечное множество |
|
|
|
обратимых циклов (РИС. 11.9). Запишем неравенство Клаузиуса для каждого из этих циклов и просуммируем эти неравенства:
|
Q |
0, |
|
|
21 |
|
|
|
|
T |
|
|
|
|
|
21 |
|
|
|
|
|
, |
|
|
|
Q |
|
|
|
|
|
|
2i |
0, |
|
T |
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
— неравенство Клаузиуса: количество приведённого тепла, полученного рабочим телом в обратимом цикле, равно нулю, а в необратимом цикле — меньше нуля.
Теперь пусть Qi → 0. Тогда при обратимом цикле
Подынтегральное выражение — функция состояния термодинамической системы;
|
δQ |
|
|
|
dS |
|
|
|
|
, |
|
|
T |
|
|
|
обрат |
|
S — энтропия; |
|
|
|
|
|
|
S |
|
Дж |
. |
|
|
|
К |
|
|
|
|
|
|
|
Приращение энтропии равно количеству приведённого тепла, полученного системой в обратимом процессе.
При необратимом процессе dS δQT .
103
Лекция 12
2.6.2. Фазовое пространство |
|
|
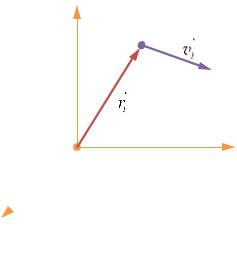
Состояние частицы определяется 6 микропара- |
z |
|
метрами: xi, yi, zi; vxi, vyi, vzi (РИС. 12.1). Микросо- |
|
|
mi |
стояние системы определяется 6N микропара- |
|
|
метрами (N — число частиц в системе). |
|
|
Фазовое пространство — 6-мерное простран- |
|
|
ство координат и проекций скоростей (импуль- |
|
|
сов). Фазовое пространство можно разбить на |
|
|
области (фазовые ячейки). Размер ячейки не |
|
|
детерминирован в классической физике, но |
O |
y |
определён в квантовой механике (см. РАЗДЕЛ |
|
|
6.1.5). |
x |
|
Изобразительная точка — точка в фазовом |
|
|
|
пространстве, эквивалентная молекуле. |
|
Рис. 12.1 |
В классической физике тождественные ча- |
|
|
стицы различимы — изобразительные точки можно пронумеровать.
Микросостояние задаётся распределением изобразительных точек (по номерам) по фазовым ячейкам.
Макросостояние задаётся количеством изобразительных точек в каждой фазовой ячейке.
2.6.3. Термодинамическая вероятность
Термодинамическая вероятность (статистический вес) W макросостояния — число микросостояний, которым может быть реализовано данное макросостояние. Термодинамическая вероятность — функция состояния системы.
Все микросостояния считаются равновероятными. Вероятность i-го макросостояния
Pi Wi , W0
где W0 — статистический вес макросистемы — число возможных микросостоя-
ний данной макросистемы.
Равновесному состоянию соответствует макросостояние, которое реализуется наибольшим числом микросостояний (статистический вес Wmax).
Любая замкнутая термодинамическая система стремится к состоянию с максимальной термодинамической вероятностью. Любой самопроизвольный термодинамический процесс идёт в сторону возрастания термодинамической вероятности.
ПРИМЕРЫ
1) Распределение четырёх изобразительных точек по двум фазовым ячейкам
Число изобразительных точек (молекул) N = 4, число фазовых ячеек n = 2 Распределение показано в ТАБЛ. 12.1.
|
|
|
|
|
104 |
|
|
|
|
|
|
|
|
|
|
|
Таблица 12.1 |
|
|
|
|
Левая |
Правая |
|
|
|
Число изобразительных точек в ячейке |
|
|
|
|
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 микросостояние |
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 микросостояния |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
С |
2 |
|
4! |
|
2 3 4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2! 4 2 ! |
|
2 2 |
|
|
|
|
|
|
|
|
|
6 микросостояний
4 микросостояния
1 микросостояние
|
Макросостояние |
Число микросостояний = |
Вероятность |
|
|
|
= статистический вес |
|
левая ячейка |
правая ячейка |
макросостояния |
|
макросостояния |
|
|
|
|
|
0 |
4 |
1 |
1/16 |
|
1 |
3 |
4 |
1/4 |
|
2 |
2 |
6 |
3/8 |
|
3 |
1 |
4 |
1/4 |
|
4 |
0 |
1 |
1/16 |
Статистический вес макросистемы
Видно, что наиболее упорядоченные макросостояния (0 и 4, 4 и 0) наименее вероятны, а наименее упорядоченное (5 и 5) — наиболее вероятно.
2) Распределение десяти изобразительных точек по двум фазовым ячейкам
N = 10, n = 2
Статистический вес макросистемы
W0 210 1024.
Наиболее вероятное макросостояние:
5 5
Статистический вес этого макросостояния
105
W |
С |
5 |
|
10! |
|
|
|
|
|
5,5 |
|
10 |
|
5! 10 |
5 ! |
|
|
|
|
Наименее вероятные макросостояния:
Статистический вес этих макросостояний
W0,10 W10,0 1.
3) Распределение 1025 изобразительных точек по двум фазовым ячейкам
N = 1025, n = 2
Статистический вес макросистемы
(Студентам предлагается самостоятельно найти вероятности отдельных макросостояний в ПРИМЕРЕ 2, вероятность наименее вероятного состояния в ПРИМЕРЕ 3.)
2.6.4. Статистический смысл энтропии
Пусть имеются две термодинамические системы, имеющие статистические веса W1 и W2. Объединим эти системы в одну. Статистический вес объединённой системы
— термодинамическая вероятность не обладает свойством аддитивности. Аддитивная величина — логарифм термодинамической вероятности:
Энтропия
S k lnW
– мера неупорядоченности термодинамической системы.
Можно доказать, что два определения энтропии — термодинамическое (см. РАЗДЕЛ 2.6.1) и статистическое — эквивалентны.
2.6.5. II начало термодинамики
II начало термодинамики указывает направление протекания термодинамических процессов. Оно не следует из фундаментальных физических законов.
Существует много формулировок II начала термодинамики, все они эквивалентны. Приведём три из этих формулировок.
1.В замкнутой (изолированной) термодинамической системе все процессы идут в сторону возрастания энтропии.
2.Невозможен термодинамический процесс, единственным результатом которого была бы передача тепла от менее нагретого тела к более нагретому.
3.Невозможен вечный двигатель II рода35, т. е. двигатель, который превращал бы всё подведённое к нему тепло в работу без каких-либо изменений в других телах.
Возможны (но маловероятны) самопроизвольные отклонения термодинамических систем от равновесного состояния — флуктуации.
35 Вечный двигатель I рода — двигатель, совершающий работу без подвода энергии.
106
2.6.6. Изменение энтропии в термодинамических процессах
В неизолированной системе энтропия может как возрастать, так и убывать.
Обратимые процессы идут при максимальной энтропии, причём
, так как приращение энтропии обусловлено
двумя процессами — подводом тепла и переходом системы к равновесному состоянию.
Равновесный адиабатный процесс — изоэнтропический процесс (δQ = 0 → dS = 0).
ПРИМЕР
Изменение энтропии идеального газа
Идеальный газ переходит из состояния с параметрами p1, V1, T1 в состояние с параметрами p2, V2, T2. Найти изменение энтропии газа.
Так как энтропия — функция состояния системы, то результат не должен зависеть от того, каким способом происходит переход из начального в конечное состояние. Перейдём из состояния 1 в состояние 2 обратимым образом. Как обсуждалось РАНЕЕ, возможны два обратимых процесса — квазистатический адиабатный и изотермический процессы. Поэтому точки 1 и 2 на диаграмме РИС. 12.2А мы соединим изотермой и адиабатой через промежуточное состояние 3:
1-3 — изотермический процесс,
3-2 — адиабатный процесс.
На РИС. 12.2Б изображены графики тех же процессов в координатах (T, S).
Рассчитаем изменение энтропии:
В изотермическом процессе 1-3 δQ = δA = pdV, а pV = p1V1
S |
|
|
3 |
pdV |
|
p V |
3 dV |
|
p V |
ln |
V |
(12.1) |
12 |
|
|
1 1 |
V |
1 1 |
3 . |
|
|
T |
|
T |
|
T |
|
V |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
1 |
|
1 |
|
107
p
Рис. 12.2
Найдём V3 из уравнений адиабатного и изотермического процессов:
p1V1 p3V3 ,
p2V2γ p3V3γ .
Разделим нижнее уравнение на верхнее:
|
|
p |
V |
γ |
V γ 1 |
|
|
2 |
2 |
3 |
|
p |
V |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
γ |
|
p |
γ 1 |
V |
γ 1 |
|
|
V |
2 |
|
2 |
|
|
|
3 |
|
p |
|
|
1 |
|
|
γ 1 |
|
1 |
V |
|
|
|
|
|
|
|
|
|
1 |
Выразим показатель адиабаты γ через число степеней свободы i молекулы:
2 |
, |
|
γ |
|
|
i 2 |
|
i |
|
|
|
|
|
|
i |
|
γ 1 |
|
i 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i 2 |
|
|
|
|
|
|
2 V |
|
2 |
. |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
V |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Подставим это выражение в формулу (12.1):
|
|
|
|
|
|
|
|
|
|
i |
|
|
i 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S12 |
|
p V |
ln |
|
p |
2 |
V |
2 |
|
|
p V |
i |
ln |
p |
|
i 2 |
ln |
V |
1 |
1 |
|
|
2 |
|
|
|
i |
1 1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
p |
|
|
|
|
|
|
|
T |
|
2 |
|
p |
|
2 |
|
|
V |
|
|
|
1 |
|
|
|
|
1 |
|
V 2 |
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как из уравнения Менделеева-Клапейрона |
p1V1 |
νR , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
S |
12 |
ν C ln p2 |
C |
p |
lnV2 |
|
p1V1 |
C ln p2 |
C |
p |
lnV2 |
|
|
|
|
V |
|
p1 |
|
|
|
V1 |
|
|
T1 |
|
|
V |
|
p1 |
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.6.7. III начало термодинамики
III начало термодинамики (тепловой закон Нернста): при стремлении к нулю термодинамической температуры энтропия термодинамической системы стремится к нулю.
Другая формулировка: абсолютный нуль недостижим.
Из закона Нернста следует, что для любой термодинамической системы
2.7. Классические распределения частиц идеального газа
2.7.1. Функция распределения
Пусть имеется термодинамическая система из N частиц; ξ — величина, характеризующая частицу. Вероятность того, что величина ξ будет иметь значение ξi,
Pi
где Ni — количество частиц, для которых
Условие нормировки:
(так как то, что величина ξ примет какое-нибудь значение из области определения, есть достоверное событие).
Среднее значение величины ξ:
Если величина ξ изменяется непрерывно, то вероятность того, что ξ = (ξ, ξ + dξ)
где f(ξ) — функция распределения вероятности (плотность вероятности).
ПРИМЕР
|
Распределение Гаусса |
|
|
|
|
|
Распределение Гаусса — это функция |
|
|
|
|
вида |
|
|
|
f(ξ) |
|
|
|
|
|
f ξ Ae α ξ ξ0 2 , |
|
|
|
|
где ξ0 — постоянная, α — положитель- |
|
|
|
|
ная постоянная; коэффициент A нахо- |
|
|
|
|
дится |
из |
условия |
нормировки |
|
|
|
|
(см. НИЖЕ). |
График |
распределения |
0 |
ξ0 |
ξ |
|
Гаусса показан на РИС. 12.3. |
|
|
|
|
|
По такому закону распределяются ре- |
|
Рис. 12.3 |
|
|
зультаты серии большого числа случай- |
|
|
|
|
ных измерений36. |
|
|
|
|
Демонстрация: Доска Гальтона
Свойства функции распределения37
1.Определённость и непрерывность во всей области определения ξ(a, b)
36Результаты серии небольшого числа случайных измерений (N 10) подчиняются распределению Стьюдента (см. ВВОДНУЮ ГЛАВУ ЛАБОРАТОРНОГО ПРАКТИКУМА).
37В «живой» лекции эти свойства можно записать математическими значками.
109
2.Дифференцируемость во всей области определения
3.Интегрируемость во всей области определения
4.Условие нормировки (нормируемость):
Зная функцию распределения, можно найти среднее значение любого параметра, зависящего от ξ.
Вероятность того, что величина ξ принимает значение от ξ1 до ξ2,
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
P ξ |
1 |
,ξ |
2 |
|
|
|
f ξ dξ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Среднее значение ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
. |
|
|
|
|
|
|
ξ |
|
|
ξf ξ dξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее значение квадрата ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
. |
|
|
|
|
ξ |
2 |
|
|
ξ |
2 |
f ξ dξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее значение функции φ(ξ)
Наиболее вероятное значение ξ
Дополнительное задание
Найти по РАСПРЕДЕЛЕНИЮ ГАУССА (a → –∞, b → ∞): нормировочный множитель A,
 ξ
ξ
 ,
,

 Q1
Q1 3
3



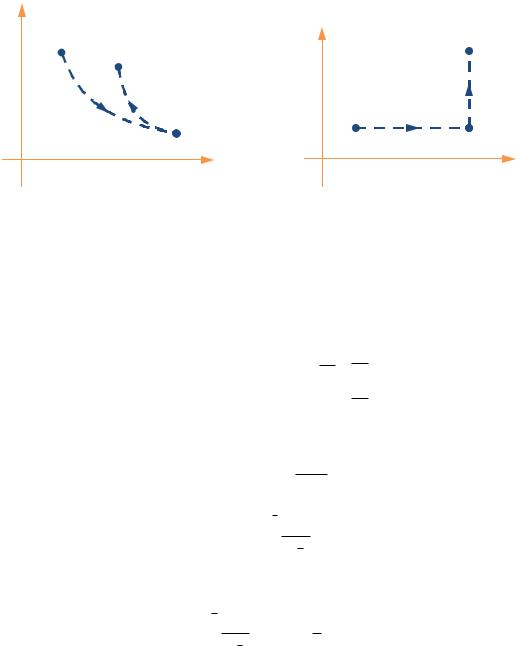



 ξ
ξ ,
,