Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

AGM_lektsii_v_2 (1)

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

3.92 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Физический смысл функции тока:

dS – элемент дуги АВ.

Скорость V проецируем на нормаль n. Найдем расход сначала найдем расход через элемент dS.

dQ=VndS (объемный расход в единицу времени)

VX cos n ^ x

VY cos n ^ y

cos n ^ x

cos

n ^ y

dQ V

V dx

X dS

Найдем расход через дугу АВ:

Q dQ

VX dy

VY dx

через дугу АВ. Для этого

Расход через кривую АВ = разности значений функции тока на концах этой кривой и не зависит от формы кривой.

Вывод:

1.Если кривая АВ является элементом линии тока, то расход через нее =0. (т.к. вдоль линии

тока ψ = const, т.е. ψА = ψВ)

2.Количество среды протекающей между двумя линиями тока на всем их протяжении есть

const

3.Расход через замкнутую кривую = 0, т.к. А и В совпадают

Функция тока, наряду с потенциальной функцией описывает потенциальное течение.

Сложение простейших потенциальных потоков.

Если есть потенциальные потоки φ1 и φ2, то они удовлетворяют уравнению Лапласа.

2	2			2	2
1	1		0	2	2		0
x2		y2		x2		y2

Рассмотрим потенциальный поток φ=φ1+φ2 и посмотри удовлетворяет ли функция φ уравнению Лапласа.

2	2		2		2		2		2
			1		1		2		2		0
x2		y2		x2		y2		x2		y2

При наложении потенциальных потоков их потенциальные функции складываются алгебраически. Найдем скорость суммарного потенциального течения

VX 1

VX 2

VY1

VY 2

При наложении потенциальных потоков их скорости складываются геометрически Сказанное выше о потенциальной функции в полной мере относится и к функции тока.

Комплексный потенциал, Комплексная скорость

Ранее мы получили:

x y

Условие Коши-Римана

y x

Условие Коши-Римана является НиДУ для существования некой аналитической функцииW(z), где z

– комплексная переменная

W (z)

x iy

dW (z)

VX iVY

(комплексная скорость)

VX iVY - сопряженная комплексная скорость

dW (z)

V 2

W(z) – комплексный потенциал или характеристическая функция, является одним из параметров так же как и вектор скорости описывающих потенциальное течение.

Простейшие потенциальные потоки

Равномерный прямолинейный поток

by , где а и b – действительные числа

a; __V

b; ___

VX dy

VY dx

ady

bdx

Семейство линий тока – прямые линии, семейство

эквипотенциальных линий – тоже семейство прямых линий (линии

тока

и эквипотенциальные линии - ортогональны)

Частные случаи:

Поток || оси Х:

ay;

Поток || оси Y:

bx;

W (z) az

a a1

a2i

z x iy

W(z) a1

a2i x iy a1x a1iy a2ix a2 y a1x a2 y i a1 y a2x

dW (z)

a VX

iVY

dW (z)

2 V

a 2

Течение внутри прямого угла.

y2 , где а – действительные числа > 0

2ax

2axdy

2axy

Тогда семейство линий тока

const

-гиперболы у

которых асимптоты – оси СК.

const

0; y

const

0; y

const

линии _ тока

оси _ СК

нулевые _ линии _ тока


	Точка соответствующая началу СК – (VX		0;VY	0 ) – критическая.
Найдем параметры потока: возьмем точку М на оси Х		VXM 2ax;	VYM	0
Семейство эквипотенциальных линий:
const	x2 y2 const - гиперболы с асимптотами – биссектрисы углов СК.

W z az2 где а – действительное число > 0, z

iy 2

2ixy

ax2

2aixy

ay2

2axy

dW (z)

2az 2a x iy

2ax i2ay

2ax;

2ay

Источник и сток

r 2

x2 y2

ln x2

ln r

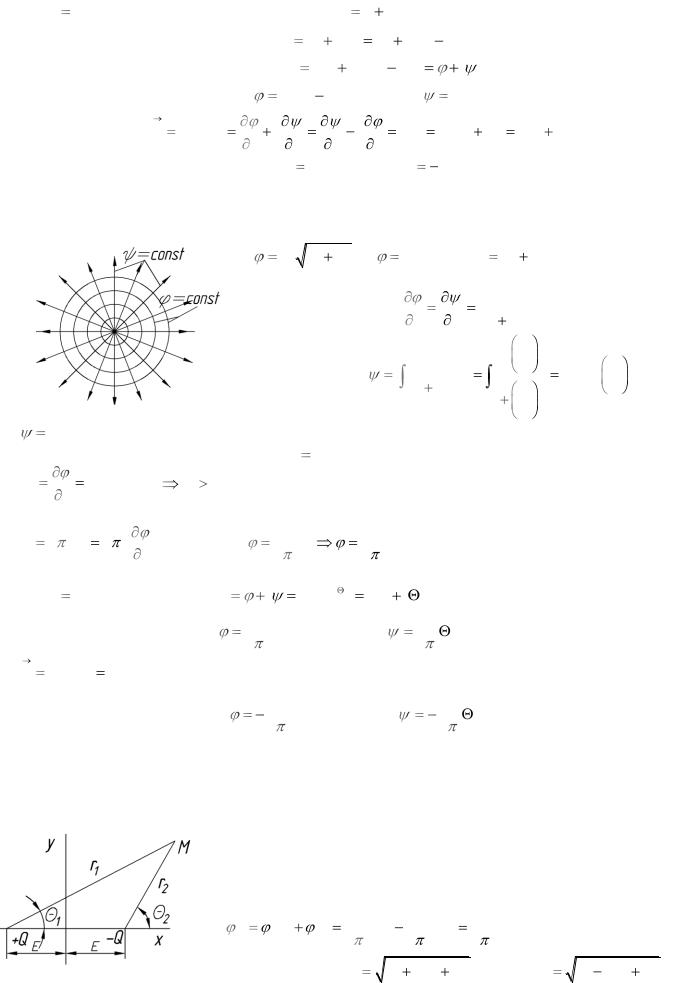
Найдем функцию тока по известной потенциальной функции:

x2 y2

arctan

y 2

const - семейство лучей из начала СК.

Семейство эквипотенциальных линий: r

const

, т.к. r>0

V 0

- течение от центра. Течение от источника, источник – начало СК.

Найдем расход Q/сек через замкнутую кривую

Q 2 rV 2 r

Q dr

ln r

W z ln z

W z

ln rei

ln r i

ln r

источник

dW (z)

ln r

сток

Диполь

Течение от диполя представляет из себя наложение двух потенциальных потоков от источника и стока.

Как известно при наложении потенциальных потоков происходит алгебраическое суммирование их потенциальных функций и функций тока.

Найдем потенциальную функцию течения от диполя:

	Q	ln r	Q	ln r	Q	ln	r1
Д ИСТ СТ
	2	1	2	2	2 r2

Из геометрии:	r	x E 2	y2	r	x E 2	y2
	1			2

Подставим:

x E 2

x2 2Ex E2

y2 4Ex

2Ex E

x E 2

4Ex

E 2

Можно представить в ряд ln(1

....

С достаточной степенью точности ограничимся первым членом при разложении в ряд.

	Q	4Ex		потенциальная функция диполя

Д 2		x E 2	y2

Определим функцию тока диполя:

ИСТ

СТ

Из геометрии:

tg 2

x E

1tg

E x

y x

2Ey

E2 y2

	z3		z5
Можно разложить в ряд: arctgz z				....
Можно разложить в ряд: arctgz z	3	5		....
	3	5

С достаточной степенью точности ограничимся первым членом при разложении в ряд.

2Ey

	1	2	x2		E2		y2
Тогда функция тока течения от диполя				Q			2Ey
		Д
			2			x2	E2 y2

Будем полагать, что при сближении источника и стока (т.е. при E 0 ) бесконечно возрастает их
мощность ( Q	) тогда величина 2QE стремится к постоянной величине – момент диполя(М).

Момент диполя направлен от стока к источнику.

Д 2 x2

2 x2

Семейство линий тока

const

- окружности касательные к оси ОХ

Семейство эквипотенциальных линий

const

- окружности касательные к оси ОН

Вихрь

ln r;

const ln r

const r const

- семейство окружностей.

течение в сторону увеличения Θ или против часовой

1 Q

r 2

стрелки.

Физический смысл Θ:

VS dS

1 Q

Q – напряженность вихревой точки (плоского вихря)

ln r;

Чисто циркуляционное обтекание цилиндра..

Не изменяя физической сущности картины течения от вихревой точки или плоскости вихря можно предположить что при некотором радиусе r0 картина представляет собой сечение бесконечно длинного цилиндра ось которого совпадает с осью OZ.

V ; r

V 0; _ VMAX

Безциркуляционное обтекание круглого цилиндра.

Результат наложения двух потенциальных течений:

равномерный прямолинейный поток || оси Х со скоростью на ∞=1

Поток от диполя с моментом 2π

;

2 x2

тогда потенциальная функция будет результатом алгебраического сложения потенциальных функций потоков 1 и 2.

;

Найдем проекции вектора скорости VX и VY

const

y x2

c x2

y2 , примем,

что с=0

уравнение нулевых

линий тока.

y 0	или x2 y2 1 0
Ось Х	окружность R=1 с центром – начало СК.
Найдем VX и VY :

V											x						x					x x x2			y2	1			1 x2			y2		1	x 2x				1 x2 y2				2
	X
				x				x							x2			y2		x
				x				x							x2			y2		x
1			1									2x2						1	x2			y2 2x2			1		y2		x2			1	x2		y2
1		x	2		y	2				x	2			y		2	2	1		x	2	y	2	2	1		x	2	y	2	2	1	x	2	y	2	2
			2			2											2							2							2						2



V									x							x				x x x2					y2	1			0 0 x 2 y						1 x2			y2	2			2xy

														2				2																											2
Y			y				y						x	2			y	2	y																					x	2		y	2	2
			y				y						x				y		y

Найдем VX и VY через полярные координаты Θ и r:

cos2

sin2

2xy

2 cos sin

При r

VX 1

0 , т.е. те параметры потока, что заданы.

Представим потенциальную функцию через Θ и r:

cos

sin

Будем считать что нулевая линия тока – окружность с радиусом =1 – поверхность круглого бесконечно длинного цилиндра.

Рассматриваем безциркуляционное обтекание круглого цилиндра:

r 1 Vr 0 - скорость направлена по касательной к цилиндру, обтекание безотрывное. Покажем, что циркуляция скорости при обтекании = 0

		1		2	1
VS dS	sin r		dS	sin r		rd 0

		r			r
				0

Т.о. мы подтвердили, что рассматриваем безциркуляционное обтекание.

r 1 Vr 0; __V VS 2 sin - закон распределения скорости по поверхности цилиндра.

Критические точки на поверхности цилиндра Θ=0 и Θ=π (точки в которых V=0)

Представим потенциальный поток аналогично вышерассмотренному, но со скоростью на бесконечности V∞ направленную в сторону противоположную оси Х.

Рассмотрим обтекание цилиндра радиусом r=r0

При этих условиях потенциальную функцию можно представить как:

V r

cos

V 1

cos

sin

r r0 Vr 0

VS 2V sin

sin

критические точки: Θ=0 и Θ=π, максимальная

скорость при

_ и _

VMAX

Максимальная скорость не зависит от радиуса цилиндра.

Циркуляционное обтекание круглого цилиндра:

Данное течение получается при сложении:

	1.	безциркуляционное обтекание:
	a.	Поток от диполя с моментом 2π
	b.	равномерный прямолинейный поток \|\| оси Х
со	скоростью на ∞=1
	2.	потенциальный поток от плоского вихря (вихревой
	точки)

		r2			Г		r2		Г
	V r	0	cos			V r	0	cos
1	V r	r	cos	2	2	V r	r	cos	2
1				2

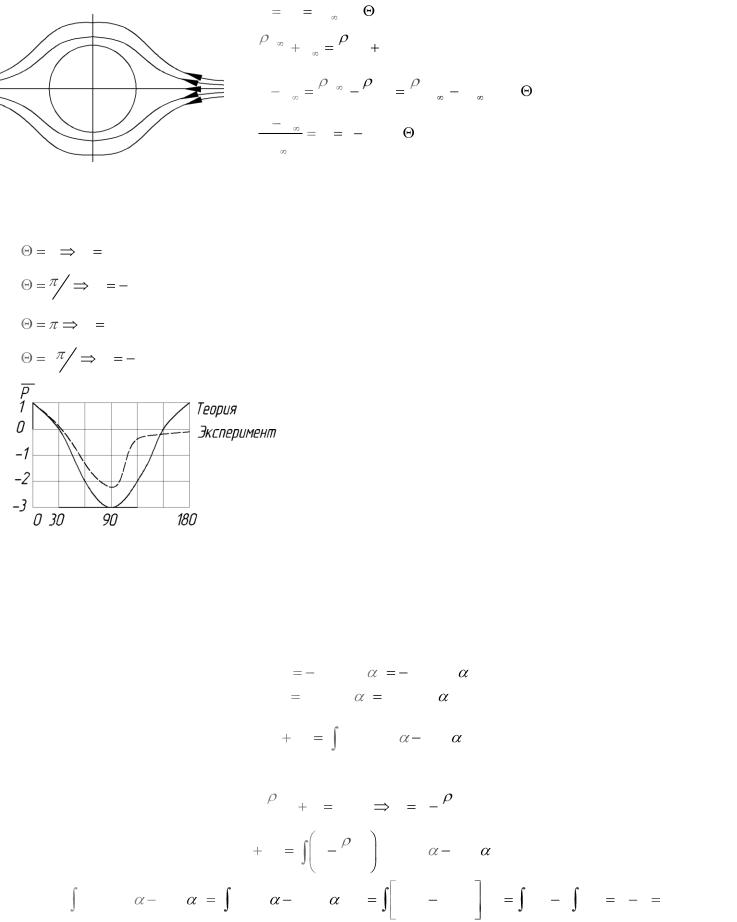
При наложении потока симметричность потока нарушается в верхней части потока скорости от вихревого течения и скорости от безциркуляционного течения складываются, а с низу вычитаются.

В связи с этим критические точки смещаются на нижнюю поверхность цилиндра:

V 1

cos

V 1

При r

Vr 0;

2V sin

Найдем положение критических точек:

sin

r0V

Пусть Г>0, тогда:

r0V

2 _ критических _ точки_ в _ III _ и _ IV _ четверти

r0V

1_ критическая _ точка_

r0V

нерасчетный _ случай _ sin_ не _ м.б.

r2		Г
0	sin
r2	sin	2 r

2 r0

Принцип Даламбера

Безциркуляционное обтекание круглого цилиндра:

VS 2V sin

V 2

4V 2 sin2

p 1 4 sin2

Давление на поверхности цилиндра не зависит не от Г не от

скорости.

__
0 p		1
	__
2	p		3
2			симметричное распределение коэффициентов давления по поверхности цилиндра
__
__
p		1
3	__
3	p		5
2	p		5
2

Рассматриваем идеальную несжимаемую среду, безотрывное обтекание цилиндра.

По принципу Даламбера: т.к. симметричное распространение давления, то результирующая сила=0

В реальной среде такого быть не может, т.к. среда вязкая и безотрывное обтекание цилиндра осуществляется крайне редко.

Представим экспериментальные и теоретические данные по изменению коэффициента давления в зависимости от Θ.

Определение результирующих сил давления при обтекании цилиндра произвольной

формы (I формула Жуковского - Чаплыгина)

Установившийся поток несжимаемой идеально среды.

PdS cos

PdS sin

PdS sin '

PdS cos

Результирующая сила:

PdS

cos

i sin

Воспользуемся уравнением Бернулли:

const

V 2

Y iX

V 2

cos

i sin

cdS cos

i sin

c cos

ci sin

dS cdx

i cdy 0 0 0

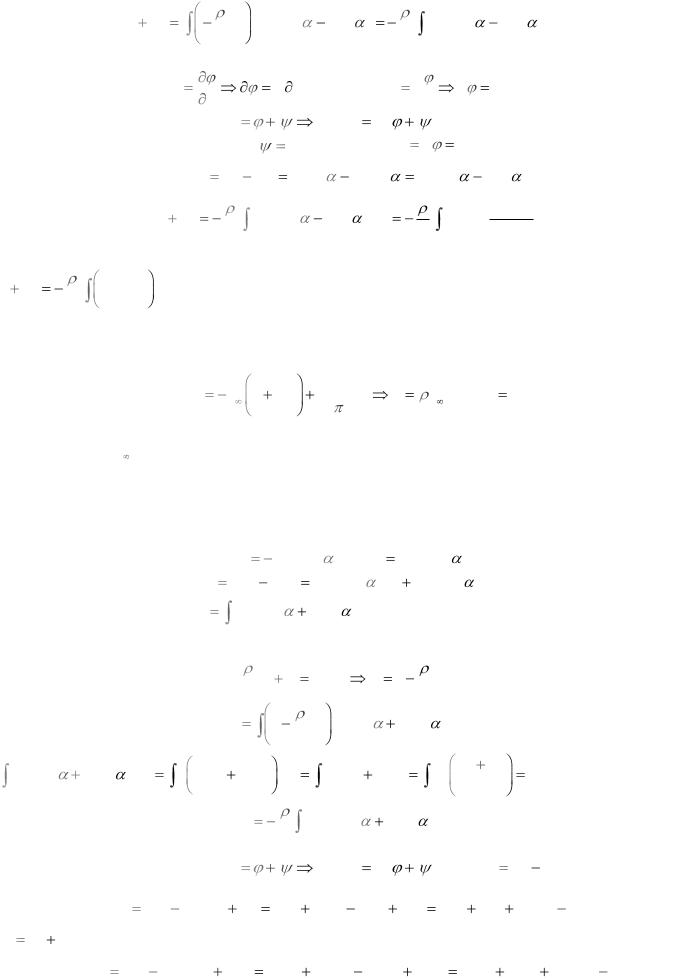
Y iX	V 2	dS cos i sin		V 2 cos i sin dS
Y iX	2	dS cos i sin	2	V 2 cos i sin dS
l				l

Т.к. мы рассматриваем безотрывное обтекание цилиндра:

	V				V S		V
		S

Характеристическая функция W(z)					i	dW(z) d
Т.к. контур l – линия тока, на которой					const , то - dW (z)
	dW (z)		VX	iVY	V cos		iV sin

	dz

Y iX				V 2	cos	i sin	dS
		2
				l

d	d	VdS

dS
dS
i
d	VdS
V	cos	i sin

dW (z) 2 l dW (z) dz

Результирующая сил давления при обтекании цилиндра произвольной формы:

		dW (z)	2
Y iX			dz - I-я формула Жуковского-Чаплыгина.
Y iX			dz - I-я формула Жуковского-Чаплыгина.
2		dz
	l

Частный случай:

Циркуляционное обтекание круглого цилиндра радиуса r.

W (z) V z	R2	i	Г	ln z Y V Г; __ X 0.
	z		2

Направление Y:

Вектор скорости V повернуть на 900 в сторону противоположную направлению Г.

Определение момента от результирующих сил давления при обтекании цилиндра

произвольной формы (II формула Жуковского-Чаплыгина)

PdS sin

___ dY

PdS cos

dYX dXY

PdS cos

PdS sin

P x cos

y sin

Воспользуемся уравнением Бернулли:

V 2

const

V 2

x cos

y sin

x cos

y sin

c xdx

ydy

0 т.к. контур замкнутый

V 2

x cos

y sin

2 l

Характеристическая функция W(z)

dW(z)

dW (z)

iVY

Вычислим z

dW (z)

x iy

V x

iV x

V y

i V

V x

idy

dW (z)

idy

V dx

iV dy

iV dx

V dy V dx

V dy

i V dy

V dx

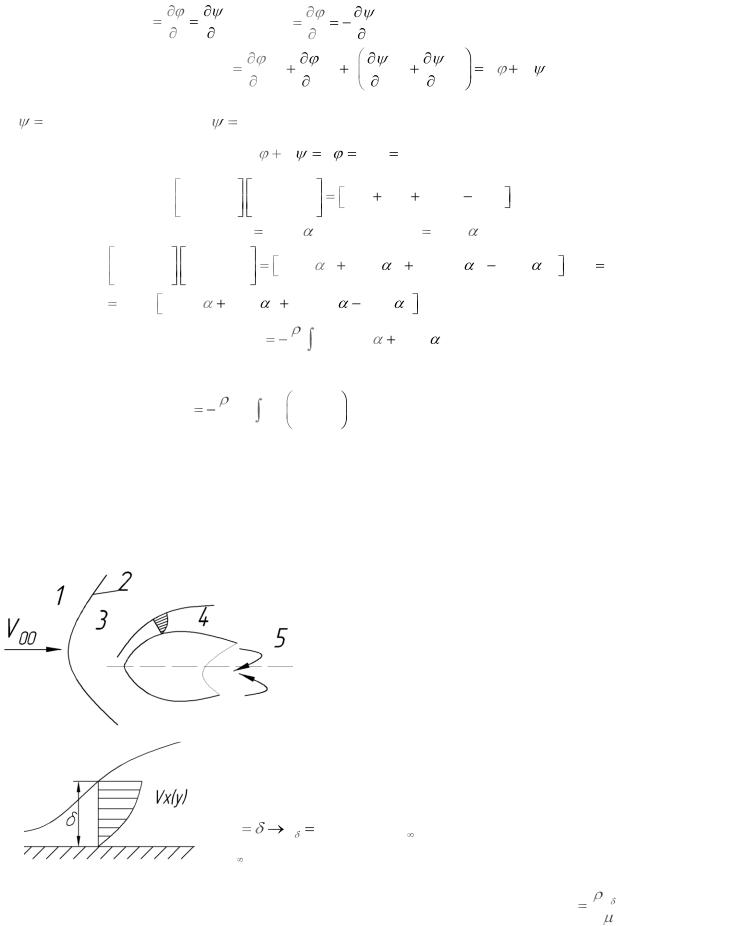
По определению: VX

dW (z)

dy i

dx d id

Т.к. l –замкнутый контур и является линией тока, и мы рассматриваем безотрывное обтекание тела,

то d 0 , т.к вдоль линии тока

const

VdS

dW (z)

x V y i V

V x VdS

V cos

V sin

dW (z)

V cos x

V sin

y i V cos

y V sin x VdS

V 2dS

x cos

y sin

y cos

x sin

V 2

x cos

y sin

zdz

dW (z)

Reцелая часть

Движение вязкой среды. Теория ПС.

Общая схема обтекания тела.

Рассмотрим обтекание тела сверхзвуковым потоком.

1.Невозмущенное изоэнтропическое течение (решение в рамках идеальной среды)

2.СУ – не имеет протяженности (в рамках идеальной сжимаемой среды)

3.Между головной ударной волной и телом (в рамках возмущенного изоэнтропического течения)

4.ПС(в рамках вязкой сжимаемой или несжимаемой среды)

5.Ближний след (в рамках вязкого потока, теория отрывных течений).

ПСпристеночный слой (прилегающий к поверхности тела) жидкости или газа в которой проявляется влияние вязкости на параметры потока.

δ – толщина ПС.

y	V	0.98...0.99 V
V - скорость внешнего набегающего потока.
Число Рейнольдса(Re) – один из основных параметров вязкой среды.			Re	V x

х – линейный размер, μ – динамическая вязкость. В зависимости от Re различные виды течения:

Ламинарное течение – слоистое течение без завихренности, отсутствие переноса количества движения из одного слоя в другой

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2015916.99 Кб9A-d_v_IGklassich.doc
#
23.03.20161.8 Mб6Accenture-Mega-Analytics-Consumer-2014-Russian.pdf
#
10.02.20154.09 Mб14AD+82.pdf
#
26.08.2019449.02 Кб3admin.doc
#
10.02.2015838.79 Кб5AG06.pdf
#
10.02.20153.92 Mб19AGM_lektsii_v_2 (1).pdf
#
09.02.2015194.31 Кб14AG_RK1_v_2013.pdf
#
23.03.2016179.62 Кб13AG_rk2_podgotovka_print.pdf
#
09.02.2015180.02 Кб31AG_RK2_v_2013.pdf
#
09.02.20151.2 Mб28algebra.doc
#
19.11.2019941.06 Кб4ALL_Лекции_Эмпт_2ч_Глот.doc