Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

AGM_lektsii_v_2 (1)

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

3.92 Mб

Скачать

☆

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Метод Характеристик.

Суть метода – решение задачи Коши.

Задача Коши.

Задана: кривая АВ в том числе и в точке М АВ, задана функция φ и x ; y

Найти: φ в точке N лежащей вне АВ и расположенной бесконечно близко к точке М АВ.

Решение:

Потенциальная функция в точке N представлена в виде ряда:

N M

				1	2					1	2				2
	M dx		M dy	1				dx	2	1				dy	2		dxdy

x		y		2		x2	M			2		y2	M			x y

Таким образом исходя из этого ряда получаем, что для нахождения потенциальной функции в точке N необходимо знать 3 векторных произведения:

Для нахождения 3-х неизвестных необходимы 3 уравнения:

тогда основное кинематическое уравнение газовой динамики как первое уравнение

системы

B VX VY

V 2

H 0

Если H≠0 – пространственное течение Если H=0 – плоское течение

2. dV		VX	dx	VX	dy
	X
		x		y		x

3. dV	VY	dx	VY	dy

Y	x		y		x

Запишем в следующем виде:

A XX		2B XY		C YY		H
dx	XX	dy	XY	0	YY	dVX
0	XX	dx	XY	dy	YY	dVY

Данная система может иметь:

1.Единственное решение – если главный определитель ≠0

(Δ≠0)

2.Неоднозначное решение либо решения не существует при

главный определитель =0 (Δ=0), т.е.	XX	YY	XY	0

Метод характеристик рассматривает случай когда Δ=0 и система имеет неоднозначное решение. Главный определитель системы выглядит следующим образом:

A dy 2

2Bdxdy C dx 2

Разделим на (dx)2

dy 2

C 0

A y'

2By'

C 0 **

Решение этого уравнения:

y'	tg			B B2 AC
		1,2	1,2
1,2				A

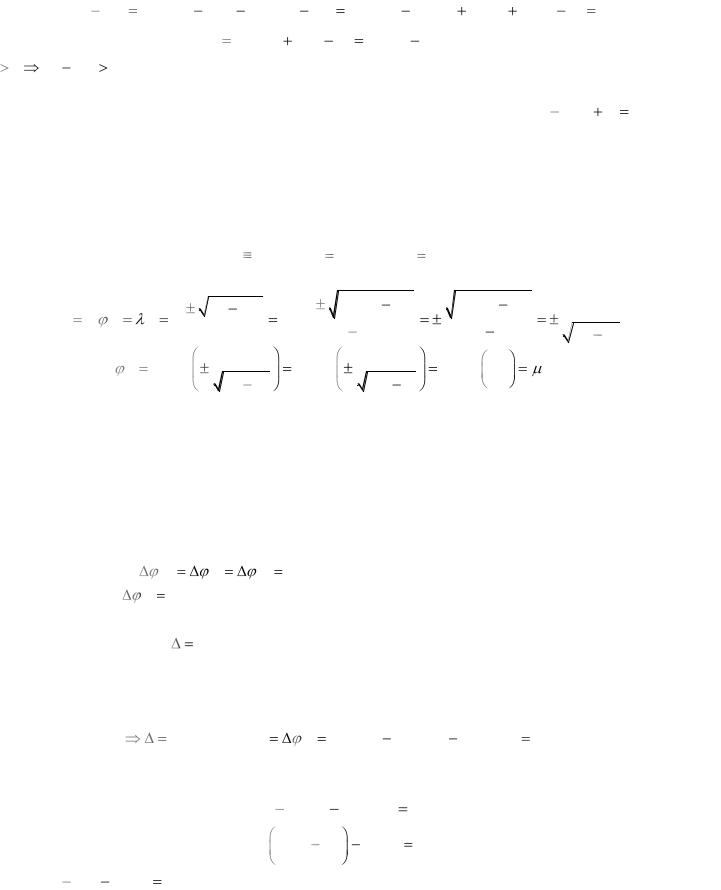
Получим 2 решения квадратного уравнения и приравняем их к нулю. Рассмотрим подкоренное выражение:

B2 AC V V

a2 V 2

V V

2V 2

a2V 2

X Y

a2 V 2	V 2	a4 a2 V 2 a2
X	Y

V a B2 AC 0

при рассмотрении сверхзвукового потока (V>a), подкоренное выражение больше нуля и решение квадратного уравнения будут 2 кривые, которые называются решением ХУ A y' 2 2By' C 0 ** в

физической плоскости. Их называют характеристиками I и II семейства Касательные, проведенные к определенной точке составляют углы φ1 и φ2.

Физический смысл характеристики в физической плоскости ( плоскость потока).

Построим вектор скорости V, и совместим ось X с вектором скорости V.

X ;

V ;

VXVY

a2 V 2

B B2

1,2

1,2 1,2

2 a2

V 2

V 2 a2

arctan

arcsin

1,2

V 2

M 2

μ-угол наклона линии малых возмущений.

Характеристики I и II семейства в плоскости потока – линии малых возмущений наклоненных к вектору V под углом μ.

Построим сетку характеристик физической плоскости (XOY) => найдем значение скорости каждой точки плоскости XOY.

Если найдем Vi и ai , то сможем найти параметры потока (Pi, Ti, ρi…)

Vi=f(A,B,C), где A,B,C – функции скорости. Т.о. недостаточно информации для построения поля скоростей. Потому обратимся к плоскости годографа скорости [VX; VY]

Из условия равенства 0 главного определителя системы следует равенство нулю частных

определителей системы.:

Выполним условие

0 :

0 dVX

, при плоском течении H=0

dy dVY

dVX

AdydVY

AdxdVX 2BdxdVY 0

dVY

dVY Ady

2Bdx

AdxdVX

0 / dx

2B AdV

dV Ay'

AdV

0 *

- характеристическое уравнение плоскости годографа скорости.

Ic. _

x; y

Ic. _ VX ;VY

dVY

A 1

AdVX

IIc. _ x; y

IIc. _ VX ;VY

dVY

A 2

AdVX

Если написать ХУ в физической плоскости [X;Y] и в плоскости вектора годографа [VX; VY], то

получим условие совместности:

A y'

2By'

Ay'

AdV

Решение уравнения совместности приводит к определению частных производных XX ;

YY ; XY , хотя

решение и неоднозначно.

XX ; YY ;

V P,T ,

Сопряженные характеристики

Сопряженные

характеристики -

Характеристики

различных семейств физической

плоскости и

Ic. _ x; y

_ и _ IIc. _ VX ;VY

плоскости годографа скорости. IIc. _

x; y

_ и _ Ic. _ VX ;VY

Свойства сопряженных характеристик

Ортогональны:

A y

2By

C 0

1, 2

2B A

Ic. _ x; y

Ic. _ VX ;VY

dVY

A 1

AdVX

0 __[2B

]

dVY

A 1

AdVX

dVY

A 1

A 2

AdVX

dVY A 2

AdVX

dVY

dVX

IIc. _ x; y

IIc. _ VX ;VY

dVY

A 2

AdVX

dVY 1

dVX 1

Условие ортогональности сопряженных характеристик:

	dy dVY			1

	dx dVX
	dx dVX

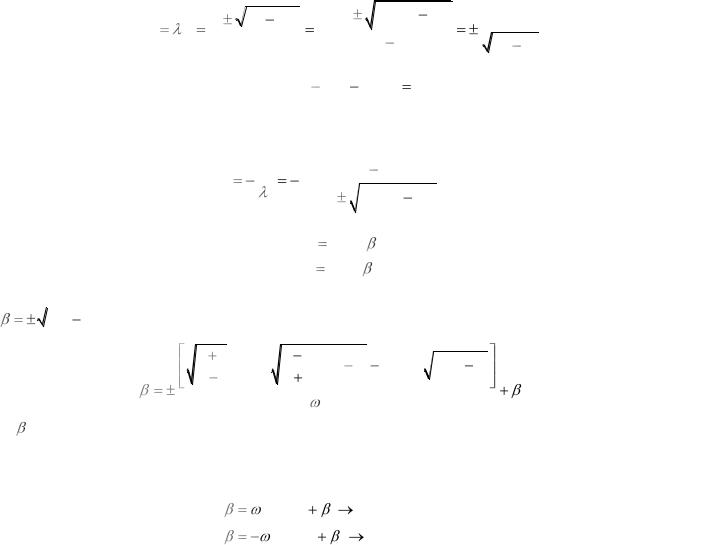
Решение характеристик в плоскости годографа скорости.

ХУ в физической плоскости [X;Y]:

A y' 2 2By' C 0

Решение ХУ имеет вид:

VXVY

a2 V 2 a2

B B2

1,2 1,2

2 a2

V 2 a2

ХУ в плоскости годографа скорости [VX; VY]:

Ay'

AdV

И ранее получено следующее равенство:

[***]

dVX

VXVY

Введем угол β – угол разворота потока:

VX	V cos
VY	V sin

Подставим VX; VY в [***] и получим ХУ в плоскости годографа скорости в виде:

		dV
d	M 2 1		, которое имеет решение:
		V

k	1		k	1
k	1	arctan	k	1	M 2 1 arctan M 2	1

k	1		k	1			1,2 ,
k	1		k	1

					k, M
					k, M

где 1,2 - постоянная интегрирования

Знак “+” ставят если характеристика I семейства Знак “--” ставят если характеристика II семейства

k, M k, M

1 Iсемейство

2 IIсемейство

Физический смысл ω(k,M)

Угол ω – угол разворота потока от направления потока соответствующего M=1 до направления потока соответствующего данному числу М.

Решение ХУ в плоскости годографа скорости [VX; VY] имеет большое прикладное значение и связано с решением задач о определении параметров потока при обтекании изломообразующей выпуклого тупого угла >1800 (Течение Прандтля-Майера).

Основные задачи решаемые методом характеристик.

История: ранее использовали графический метод на свойстве ортогональности сопряженных характеристик. Далее использовали конечные разности.

1.определение поля скоростей между кривой и характеристиками различных семейств проведенных из ее концов

2.Определение скорости в точке пересечения любого семейства с твердой стенкой.

3.Взаимодействие характеристики и СУ

Задача:

В физической плоскости кривая АВ в каждой точке которой задана скорость по величине и направлению, проведены характеристики из концов этой кривой

Нужно: определить поле скоростей в области ACB.

Графическим методом: Разбиваем АВ на бесконечно малые отрезки, стоим секу и находим поле скоростей

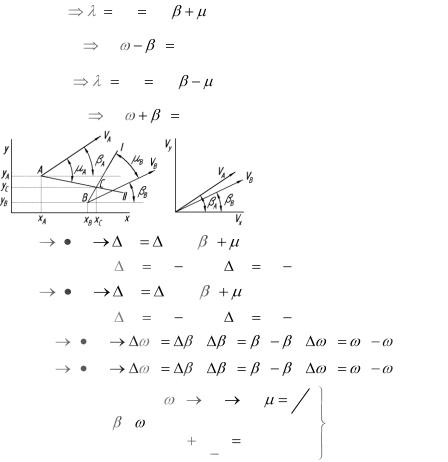
Методом конечных разностей:

Найти скорость в точке пересечения характеристик различных семейств проведенных из двух точек бесконечно близко расположенных друг к другу.

Т.к. характеристики расположены бесконечно близко, то заменим их касательными, т.е. прямыми.

Ic. _ x; y		dy		tg
	1
		dx


Ic. _ VX ;VY	d			0
IIc. _ x; y			dy	tg
	2
			dx


IIc. _ VX ;VY	d			0

x; y

xAtg

yA __ xA

x; y

xBtg

yB __ xB

VX ;VY

A ;

VX ;VY

B ;

sin

Находим xC ; yC ;

C ;

C ,

const

Течение Прандтля-Майера

обтекании изломообразующей выпуклого тупого угла >1800 поток в области 1 || твердой стенке; проходя веер волн разряжения поток

расширяется и в области 2 || стенке. В веере волн разряжения первая линия малых возмущений под углом μ1 к твердой стенке в области 1, последняя под углом μ2 к твердой стенке в области 2.

С чем связан веер волн разряжения:

Поток инерционен, и не может мгновенно развернуться из 1 в 2. Постепенное изменение направления потока происходит в веере волн разряжения.

На основании течения Прандтля-Майера 2 задачи: (изоэнтропическое течение)
1.	Прямая задача: конфигурация потока известна (β, все параметры потока в области 1), найти
параметры в области 2.
a.	P1, ρ1,		T1,				M1…					параметры				при изоэнтропическом						течении с	помощью
															k
				P						k	1			2	k 1
газодинамических функций.				1			1						M	2		P
газодинамических функций.							1						M			P
				P01							2		1			01
				P01							2
																	k	1		k	1
b.	Зная значение M можем найти ω															1	k	1	arctan	k	1	M 2 1 arctan		M 2	1
b.	Зная значение M можем найти ω																		arctan			M 2 1 arctan		M 2	1
							1								1		k	1		k	1		1
																	k	1		k	1
	c.									2			1
										2			1
	Зная значение ω2 можем найти M2 по той же формуле.
	d.							Т.к. среда не вязкая, трения нет, нет диссипации энергии, то P01=P02
												k
		P2	1		k		1 M 2					k 1		P
												k 1
									2					2
		P02				2			2					2
		P02				2

И далее все интересующие параметры.

2.Обратная задача Течения Прандтля-Майера: задано P2, но не задано β, Найти β.

k 1

a) _

b) _

P01

c) _ P01

P02

M 2

d ) _ M 2

e) _ 2 1

P02

Каков max угол отклонения потока и как его определить:

arctan

M 2

arctan M 2 1

Vmax

; __ k

1.4; __

max

130.46`

Метод малых возмущений. Метод линеаризации.

Область применения: как дозвук, так и сверхзвук, обтекание плоского тела при малых углах атаки. Математическая суть: во всех уравнениях и выражениях величины не выше 1-го порядка малости. Возмущенные области при обтекании.

` V

VX` и VY` - бесконечно малые обусловленные возмущениями у поверхности тела.

VY `

V 2

` V

V ` 2

V 2

` 2

2V V

` V ` 2

V 2

2V V

Основное кинематическое уравнение газовой динамики:

VX	V	2	a2	VY	V 2	a2	V V	VX	VY	0

x	X			y	Y		X Y	y	x

Найдем a2 в возмущенной области и на ∞:

V 2

max

k 1

V 2

k 1

V 2 2V V

max

a2 a2

k 1

V 2

2V V `

k 1

2 V 2

k 1

max

1 V V `

Подставим а2 в основное кинематическое уравнение газовой динамики:

V 2

a2 V V

` V

V V `

k 1 V V `

V 2

2V V ` V ` 2

k 1 V V `

VX `

V ` 2

a2 k 1 V V `

VY `

V 2

VX `

VY `

M 2 1

VX `

2V VX `

VX ` V VY			`	VX	VY	0
VX ` V VY			`	y	x	0
				y	x
VY	`	0
y		0
y

Линеаризованное уравнение газовой динамики.

		2		2
`	M	2 1				0
			x2		y2

Решая это уравнение и находя потенциальную функции φ в возмущенном потоке мы решаем задачу о нахождении АД характеристик.

Пример:

dyВ PВ P dx dyH PH P dx dy dyH dyВ

Используем уравнение Бернулли для несжимаемой среды (ρ=const):

V 2 P			const
2

Для условий невозмущенного и возмущенного потока у поверхности профиля:

V 2

P V 2

__ V 2

V 2

2V V

P P

V 2

V VX `

P P

B ` ___ P

H `

Найдем АД характеристики профиля в виде АД характеристики – коэффициент нормальной силы:

H `

B `

d x

d x__ d x

V 2

Подходы к решению линеаризованного уравнения ГД.

Как известно метод линеаризации рассматривается как при дозвуке, так и при сверхзвуке.

					2					2
1.	M 1	M 2		1									0 *
1.	M 1	M 2		1		x2					y2		0 *
						x2					y2
																		2		2
Используем новые переменные и сведем это уравнение к уравнению Лапласа.																						0
																			x2		y2	0
																			x2		y2
														2				2

				x		x								x2				x 2
					1													1
												y1
												y1					1 M 2
																	1 M 2
			y	y1								y			y1
		2									y1			2
											y1					1		M 2
			y2		y y						y			y	2	1		M 2
			y2		y y						y			y	2
					1									1
					2					2
			M	2	1									1		M 2		0
			M		1		x		2			y 2		1		M 2		0
							x		2			y 2
					1					1
					2					2
														0
								x	2			y	2	0
								x	2			y	2
					1					1

Мы свели уравнение [*] при дозвуковом течении к уравнению Лапласа, которое описывает несжимаемую среду.

При переходе [x;y] [x1;y1] означает переход к модели течения описывающую несжимаемую среду. Так же решение задачи в [x1;y1] приводит к изменению формы профиля и изменению угла под

которым обтекается профиль.

2.M 1

Уравнение [*] к уравнению Лапласа свести невозможно, но подход к решению уравнения при сверхзвуке состоит так же в введении новых переменных.

		y xtg		y xtg		tg	1


							M 2 1
							M 2 1
Подставляя эти переменные в [*] получим
			2
Решение этого уравнения имеет вид:					0[**]
					0[**]

` f1	f2	, вид функций f1 и f2	определяется условиями конкретной задачи и ее граничными

условиями.

Распространенный случай решения:

Обтекание двух тупых углов линеаризованным потоком:

В отличии от решения Прандтля-Майера (точное решение обтекания выпуклого тупого угла) где поток разворачивается от потока 1 к 2 проходя веер волн разряжения. В данном случае т.к. угол β мал, то образуется только одна линия малых возмущений с углом μ1.

При рассмотрении a и b область с индексом ∞ заменяется на 1, где все параметры потока известны. Принципиально случаи a и b отличаются только знаком Δβ, т.е. в возмущенной области 2 параметры

потока различны, но подход к определению параметров в этих областях в рамках метода линеаризации одинаков.

Решение φ` принимаем в виде:

		`	f1	f2	f2	0
			`	f1	V1 y xtg
VX	`	`	V1tg		VY `	`	V1

		x				y
		x				y

Как видно знаки скоростей определяются возмущением и в том числе зависят от знака Δβ.

1)	0	VX `	0;	VY `	0
2)	0	VX `	0;	VY `	0

Найдем коэффициент давления в возмущенной области 2:

__ P		P
2		1
d P2
		q1

P P мы уже ранее находили для несжимаемой среды (из уравнения Бернулли), этот же результат

2 1

верен и для сжимаемой среды.

P	1V1VX `			2VX `		2V1tg 1		2tg		2
__
2		V12			V1		V1		1
2		V12			V1		V1		1		M 2	1
	1	2									1
		2

			__
1) ___		0	P		0 _ течение _ разряжения _ P					P _ V		V
			2						1	2	1	2
			__
2) ___		0	P		0 _ течение _ сжатия ____ P					P _ V		V
			2						1	2	1	2

Плоское потенциальное движение несжимаемой идеальной среды.

Условие потенциального потока:

Z 0

VX VZ

НиДУ для того что бы полный дифференциал некоторой функции φ был равен:

d VX dx VY dy VZ dz , где функция φ – потенциальная функция описывающая потенциальное

течение. Но по определению d

dz ,

от сюда

связь проекций скорости на

соответствующие оси с потенциальной функцией

; __VY

; __VZ

;

Т.к. мы рассматриваем плоское потенциальное течение, то условие потенциальности имеет вид:

pVX

pVY

Уравнение неразрывности:

0 , для несжимаемого потока имеет вид:

Введем функцию ψ, которая удовлетворяет условию неразрывности.

Функция ψ – функция тока.

VX dy VY dx

dx d

При интегрировании ψ = const

Ψ –характеризует семейство линий тока и вдоль линии тока ψ = const

Если существует семейство линий тока, вдоль каждой из которых ψ = const, то можно предположить, что существует семейство кривых вдоль которых потенциальная функция есть величина постоянная.

Это семейство называется – семейство эквипотенциальных линий. φ(x,y) = const – уравнение эквипотенциальных линий.

Можно проследить связь между потенциальной функцией и линией тока:

0 __ VX VY VXVY 0

x x y y

Условие ортогональности кривых.

Т.о. семейство линий тока ортогонально эквипотенциальным линиям.

Рассмотрим условие потенциальности:

VY	VX	0
x	y

Подставим выражения проекций VX и VY через функцию тока:

0 Уравнение Лапласа.

Т.о. функция тока удовлетворяет уравнению Лапласа.

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2015916.99 Кб9A-d_v_IGklassich.doc
#
23.03.20161.8 Mб6Accenture-Mega-Analytics-Consumer-2014-Russian.pdf
#
10.02.20154.09 Mб14AD+82.pdf
#
26.08.2019449.02 Кб3admin.doc
#
10.02.2015838.79 Кб5AG06.pdf
#
10.02.20153.92 Mб19AGM_lektsii_v_2 (1).pdf
#
09.02.2015194.31 Кб14AG_RK1_v_2013.pdf
#
23.03.2016179.62 Кб13AG_rk2_podgotovka_print.pdf
#
09.02.2015180.02 Кб31AG_RK2_v_2013.pdf
#
09.02.20151.2 Mб28algebra.doc
#
19.11.2019941.06 Кб4ALL_Лекции_Эмпт_2ч_Глот.doc