
- •ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВАЯ ОПТИКА
- •1. Тепловое излучение
- •2. Закон Кирхгофа. Абсолютно черное тело
- •3. Закон Стефана – Больцмана и закон Вина. Формула Рэлея – Джинса
- •4. Формула Планка
- •5. Явление внешнего фотоэффекта
- •6. Опыт Боте. Фотоны
- •7. Излучение Вавилова – Черенкова
- •8. Эффект Комптона
- •ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ
- •10. Вероятностный характер волн де-Бройля. Волновая функция
- •11. Принцип неопределенности
- •12. Уравнение Шредингера
- •13. Частица в потенциальной яме
- •14. Потенциальная яма конечной глубины
- •15. Принцип соответствия в квантовой механике
- •17. Движение свободной частицы
- •18. Гармонический осциллятор

15. ПРИНЦИП СООТВЕТСТВИЯ В КВАНТОВОЙ МЕХАНИКЕ
Критерий, при выполнении которого классическая физика дает достаточную точность и необязательно применять формулы квантовой механики, может быть записан в виде
L >> λ ,
где L – размеры системы, в которой движется частица; λ – длина волны де-Бройля.
Смысл его заключается в том, что при длинах волн, много меньших размеров системы, квантово-механические особенности в поведении частиц оказываются несущественными.
Продемонстрируем это утверждение на примере частицы в потенциальной яме (см. разд. 13). Ψ-функцию частицы (13.5), учитывая, что sin x = = (1 2i)(eix −e −ix ), можно записать в виде
æ |
|
1 ö |
|
|||
yn( x) = ç |
|
|
|
|
÷(exp(ipnx/l) - exp(-ipnx/l)). |
(15.1) |
|
|
|
|
|||
|
|
|||||
è i |
|
2l ø |
|
|||
Такое представление позволяет говорить о двух движущихся навстречу друг другу волнах де-Бройля. Сравнивая (15.1) с выражением для одномерной волны де-Бройля (9.2), получим выражение для импульса частицы для каждой из этих волн
p = πn/l
и для длины волны де-Бройля:
λ = 2π / p= 2l / n.
Очевидно, что при n → ∞, λ → 0 и поведение частицы должно быть близким к классическому.
Проследим, как это отразится на спектре энергии частицы и ее волновых функциях. Оценим расстояния между соседними уровнями энергии частицы:
En = En+1 − En = 2π2(2n+1)/2ml2.
Относительное расстояние между уровнями
En / En = (2n+ 1)/n2 → 0.
При n → ∞ спектр энергии частицы получается почти непрерывным.
52

Посмотрим теперь, как ведет себя плотность вероятности для частицы при больших n. Для классической частицы плотность вероятности постоянна и равна
|
|
|
|
|
|
|
|
|
|
|
|
dPкл/dx= 1/l |
(15.2) |
||||
Плотность |
|
вероятности (15.2) |
|
|
y |
|
2 |
|
|||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянна |
|
|
и |
|
|
удовлетворяет |
|
|
10 |
|
|
|
|||||
|
|
|
|
2/l |
|
||||||||||||
условию нормировки |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Классическая |
|||||||||
l |
|
|
|
|
l |
|
|
|
|
|
|
1/l |
|||||
dP |
|
|
dx/l =1 |
. |
вероятность |
||||||||||||
ò |
|
= |
ò |
||||||||||||||
|
кл |
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Поведение |
плотности ве- |
0 |
|
|
l |
||||||||||||
роятности при больших n пока- |
|
|
|
|
|
Рис. 15.1 |
|||||||||||
зано на рис. 15.1 (n = 10). Вид- |
|
|
|
|
|
|
|||||||||||
но, что значение |
|
ψ |
|
2 |
колеблется около среднего значения 1/l. Физический |
||||||||||||
|
|
||||||||||||||||
|
n |
|
|
||||||||||||||
смысл в этом случае имеет лишь среднее значение плотности вероятности.
Поэтому при n >> 1 |
|
ψn |
|
2 1/ l , т. е. квантовая вероятность переходит в класси- |
|
|
ческую.
Таким образом, по мере возрастания n частица все более утрачивает квантовые свойства, и при больших значениях n квантовая физика переходит в классическую.
Полученный результат является частным случаем общего физического принципа – принципа соответствия: любая новая теория, претендующая на большую общность, чем классическая теория, обязательно должна переходить в старую, классическую теорию в тех случаях, в которых последняя была построена и многократно проверена экспериментально.
16. ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ БАРЬЕР.
ТУННЕЛЬНЫЙ ЭФФЕКТ
Пусть частица, движущаяся слева направо, встречает на своем пути потенциальный барьер высотой U0 и шириной l (рис. 16.1).
По классическим представлениям, поведение частицы имеет следующий ха- U0 рактер. Если энергия частицы больше высоты барьера ( E > U0), то частица бес-
I |
II |
III |
E |
|
53 |
0 l x
Рис. 16.1

препятственно проходит над барьером и на участке 0 ≤ х ≤ l лишь уменьшается скорость частицы. Затем при х > l скорость принимает первоначальное значение. Если же E < U0, то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
Совершенно иначе выглядит поведение частицы согласно квантовомеханическому описанию. Даже при E < U0 имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области х > l. Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из уравнения Шредингера.
Рассмотрим случай E < U01. Для областей I и III (U = 0) уравнение Шредингера имеет вид
d2ψ/dx2 + (2m/ 2)Eψ = 0. |
(16.1) |
Для области II (U =U0 и E −U0 < 0) уравнение имеет вид |
|
d2ψ /dx2 + (2m/ 2)(E −U0)ψ = 0. |
(16.2) |
Положим, что решение уравнения (16.1) имеет следующий вид: |
|
ψ = exp(λx) .
Тогда подстановка этой функции в уравнение (16.1) приводит к характеристическому уравнению
λ2 + 2mE/ 2 = 0,
где λ = ±iα и α = 
 2mE/ 2 .
2mE/ 2 .
Общее решение уравнения (16.1) имеет следующий вид: ● для области I:
ψ1 = A1exp(iαx) + B1exp(−iαx);
● для области III:
ψ3 = A3exp(iαx) + B3exp(−iαx) .
Решив подстановкой ψ = exp(λx) уравнение (16.2), получим общее решение этого уравнения для области II в виде ψ2 = A2 exp(−βx) + B2 exp(βx), где
β = 
 2m(U0 − E) / 2 .
2m(U0 − E) / 2 .
1 Прямоугольный барьер называется высоким, если энергия частицы Е меньше высоты U0 потенциального барьера, в противном случае барьер называется низким.
54

Заметим, что решение вида exp(iαx) соответствует волне, распространяющейся в положительном направлении оси х, а решение вида exp(−iαx) волне, распространяющейся в противоположном направлении.
В области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо. Поэтому коэффициент B3 в выражении для ψ3 следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся стандартными условиями, которым должна удовлетворять Ψ-функция,
ψ1(0) = ψ2(0) и ψ2(l) = ψ3(l);
dψ1(0)/dx= dψ2(0)/ dx и dψ2(l)/dx= dψ3(l)/dx.
Из этих условий вытекают соотношения
|
|
|
A1 + B1 = A2 + B2 ; |
|
|
|
|
|
ü |
|
||||||
A |
|
|
exp(-bl) + B |
2 |
exp(bl) = A |
3 |
exp(ial); |
ï |
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
ï |
(16.3) |
||||
|
|
|
iaA1 - iaB1 = -bA2 + bB2 ; |
|
|
ý ; |
||||||||||
|
|
|
|
|
ï |
|
||||||||||
- bA |
|
exp(-bl) + bB |
2 |
exp(bl) = iaA |
3 |
exp(ial).ï |
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
þ |
1 1 1, |
|||
Разделим все уравнения (17.3) на 1 и введем обозначения |
||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
b = B / A |
|
a2 = A2 / A1 , b2 = B2 / A1, a3 = A3 / A1 и n = β /α = |
|
|
. Тогда уравнения (16.3) |
|||||||||||||
(U 0 |
− E) / E |
|||||||||||||||
примут вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ b1 = a2 + b2 ; |
|
|
|
|
|
|
ü |
|
|||||
a2 exp(-bl) + b2 exp(bl) = a3 exp(ial); |
ï |
|
||||||||||||||
ï |
(16.4) |
|||||||||||||||
|
|
|
i - ib1 = -na2 + nb2 ; |
|
|
|
|
|
ý ; |
|||||||
|
|
|
|
|
|
|
|
ï |
|
|||||||
- na |
2 |
exp(-bl) + nb |
2 |
exp(bl) = ia |
3 |
exp(ial).ï |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
þ |
|
||||
Количественно эффект туннелирования можно оценить, вычислив плотность вероятности ΨΨ обнаружения частицы в каждой из областей пространства. Оценим степень прозрачности потенциального барьера.
В случае пренебрежения отраженными волнами на границах I – II и II – III, отношение квадратов модулей амплитуд отраженной и падающей волн определяет вероятность отражения частицы от потенциального барьера и может быть названо коэффициентом отражения:
R = B1 2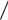
 A1 2 = b1 2.
A1 2 = b1 2.
55
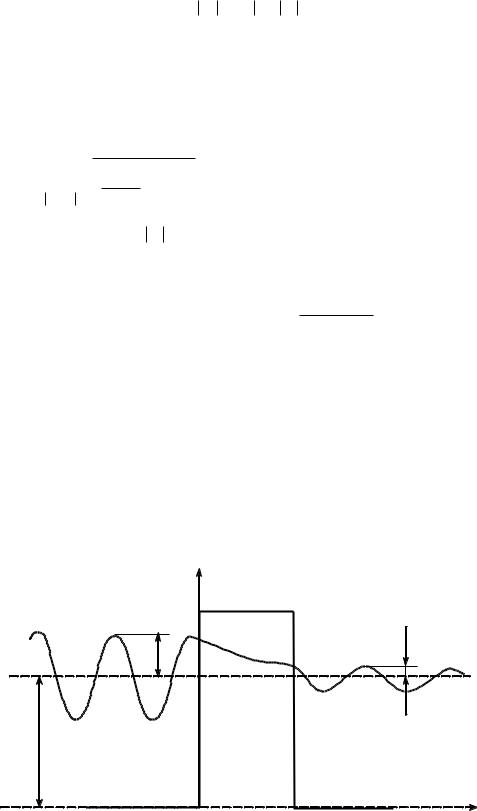
Отношение квадратов модулей амплитуд прошедшей и падающей волн определяет вероятность прохождения частицы через барьер и может быть названо коэффициентом прохождения (или коэффициентом прозрачности):
D = A3 2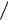
 A1 2 = a3 2.
A1 2 = a3 2.
Коэффициенты отражения и прозрачности связаны соотношением
D + R = 1.
В результате решения системы уравнений (16.4), получается
a3 = (4niexp(−iαl))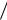 ((n+ i)2 exp(−βl) − (n− i)2 expβl).
((n+ i)2 exp(−βl) − (n− i)2 expβl).
Значение βl = l
 2m(U0 − E) / 2 обычно бывает больше единицы, поэтому, учитывая, что n −i =
2m(U0 − E) / 2 обычно бывает больше единицы, поэтому, учитывая, что n −i =
 n2 +1, получим
n2 +1, получим
D = a3 2 = (16n2 (n2 +1)2)exp(−2βl) .
(n2 +1)2)exp(−2βl) .
Отношение 16n2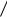 (n2 +1)2 имеет значение порядка единицы. Поэтому окончательно можно считать, что
(n2 +1)2 имеет значение порядка единицы. Поэтому окончательно можно считать, что
D ≈ exp(−2βl) = exp(− (2l / )
 2m(U0 − E)).
2m(U0 − E)).
Из полученного выражения следует, что вероятность прохождения частицы через потенциальный барьер зависит от ширины барьера l и от разности энергий (U0 − E ).
Если при какой-либо ширине барьера коэффициент прохождения D равен 0,01, то при увеличении ширины в два раза D станет равным
0,012 = 0,0001, т. е. уменьшится в 100 раз. Тот же эффект вызвало бы возрас-
тание в четыре раза |
значения |
(U0 − E ). Коэффициент прохождения резко |
|
уменьшается при увеличении массы частицы m. |
|
||
I |
U(x) |
II |
III |
Падающая волна |
U0 |
|
A1 |
Прошедшая волна
A3 |
Е Ψ (x) = A |
eiαx |
ψ |
2 |
(x) = A e–βx |
ψ |
3 |
(x) = A eiαx |
|
1 |
1 |
|
|
2 |
|
3 |
||
0 |
l |
x |
56

Рис. 16.2
На рис. 16.2 изображены: в области I – действительная часть падающей волны ( ReA1exp(iαx)); в области II – экспоненциально убывающая Y-функ- ция (ψ2 = A2 exp(−βx)) и в области III – действительная часть прошедшей волны ( ReA3 exp(iαx) ). Построение выполнено при условии пренебрежения отраженными волнами на границах I – II и II – III, при этом и
.
В случае потенциального барьера произвольной формы (рис. 16.3) коэффициент прозрачности определяется более общей формулой
D ≈ exp(−(2 / ))bò
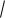 2m(U (x) − E)dx ).
2m(U (x) − E)dx ).
a
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем рассмотренное нами явление называют туннельным эффектом. На основе этого эффекта построены многие современные приборы, например туннельные диоды и транзисторы.
U(x) |
|
|
|
|
|
E |
|
|
|
U(x) |
|
|
|
|
|
|
|
|
|
|
E |
U0 |
II |
|
|
|
I |
||
0 |
a |
b |
x |
0 |
x |
|
|
Рис. 16.3 |
|
||
|
|
|
Рис. 16.4 |
||
Рассмотрим случай, когда E > U0 (рис. 16.4). Для области I уравнение Шредингера имеет вид
d2ψ /dx2 + (2m/ 2)Eψ = 0, |
(16.5) |
для области II |
|
d2ψ /dx2 + (2m/ 2)(E −U0)ψ = 0. |
(16.6) |
Общие решения уравнений (16.5) и (16.6) имеют следующий вид: ● для области I
ψ1 = A1exp(iαx) + B1exp(−iαx);
● для области II
ψ2 = A2exp(iα2x) + B2exp(− iα2x) ,
57

где α=
 2mE 2 и α2 =
2mE 2 и α2 = 
 2m(E −U0)
2m(E −U0)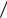 2 .
2 .
Заметим, что, как и в случае высокого потенциального барьера, решение вида exp(iαx) соответствует волне, распространяющейся в положительном направлении оси х, а решение вида exp(−iαx) – волне, распространяющейся в противоположном направлении.
В области II имеется только волна, прошедшая над барьером и распространяющаяся слева направо. Поэтому коэффициент B2 в выражении для ψ2 следует принять равным нулю. Для нахождения остальных коэффициентов можно воспользоваться стандартными условиями, которым должна удовлетворять функция ψ:
ψ1(0) = ψ2(0); dψ1(0)/dx= dψ2(0)/dx. |
(16.7) |
||||||
В области II E > U0 , следовательно, |
|
действительная |
часть волновой |
||||
функции ψ2 (ReA2exp(iα2x) = A2cosα2x) |
представляет собой |
косинусоиду с |
|||||
волновым числом |
|
|
|
|
|
|
|
α = |
|
|
|
|
. |
|
|
2m(E −U |
0 |
) |
2 |
|
|||
2 |
|
|
|
|
|
|
|
При U0 = 0 длина волны (волновое число α2) действительной части Ψ-функции в области II совпадает с длиной волны действительной части волновой функции в области I. С ростом U0 значение волнового числа α2 уменьшается (длина волны увеличивается), и в пределе при U0 = E действительная часть волновой функции в области II перестает быть гармонической.
На рис. 16.5 изображены |
действительная часть падающей волны ( |
||||||||
ReA1exp(iαx) = A1cosαx) и |
действительная |
часть прошедшей волны ( |
|||||||
ReA2 exp(iα2x) = A2 cosα2x). |
|
|
|
|
|
|
|
||
I |
|
|
|
U(x) |
II |
Прошедшая волна |
|||
Падающая волна |
|
|
|||||||
|
|
|
|
|
|
|
|||
2A |
|
|
|
|
|
|
2A2 |
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
ψ |
|
iαx |
|
|
|
|
|
|
|
|
|
|
|
|
iα2x |
||||
|
|
1 |
|
|
|
|
|||
(x) = A e |
|
|
|
ψ |
|
||||
1 |
1 |
|
|
|
|
2(x) = A2e |
|
|
|
Е |
|
|
|
U0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
x |
58
