
- •ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВАЯ ОПТИКА
- •1. Тепловое излучение
- •2. Закон Кирхгофа. Абсолютно черное тело
- •3. Закон Стефана – Больцмана и закон Вина. Формула Рэлея – Джинса
- •4. Формула Планка
- •5. Явление внешнего фотоэффекта
- •6. Опыт Боте. Фотоны
- •7. Излучение Вавилова – Черенкова
- •8. Эффект Комптона
- •ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ
- •10. Вероятностный характер волн де-Бройля. Волновая функция
- •11. Принцип неопределенности
- •12. Уравнение Шредингера
- •13. Частица в потенциальной яме
- •14. Потенциальная яма конечной глубины
- •15. Принцип соответствия в квантовой механике
- •17. Движение свободной частицы
- •18. Гармонический осциллятор
òΨΨ dV =1 |
(12.6) |
Условие (12.6) называется условием нормировки. Функции, удовлетворяющие этому условию, называются нормированными. В дальнейшем мы всегда будем полагать, что рассматриваемые нами Ψ-функции являются нормированными. В случае стационарного силового поля справедливо соотношение
ΨΨ =ψ exp(i(E / )t)ψexp(−i(E / )t) =ψψ ,
т. е. плотность вероятности волновой функции равна плотности вероятности координатной части волновой функции и от времени не зависит.
Свойства Ψ-функции: она должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек) и иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.
В уравнение Шредингера в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида Hψ=Eψ имеют решения, удовлетворяющие стандартным условиям, не при любых, а лишь при некоторых определенных значениях параметра (т. е. энергии Е). Эти значения называются собственными значениями. Решения, соответствующие собственным значениям, называются собственными функциями. Нахождение собственных значений и собственных функций, как правило, представляет собой весьма трудную математическую задачу. Рассмотрим некоторые наиболее простые частные случаи.
13. ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
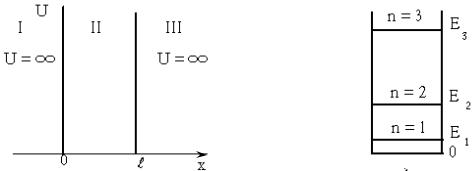
Найдем собственные значения энергии и соответствующие им собственные волновые функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме (рис. 13.1, а). Предположим, что частица
46
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E3 |
|
|||
|
|
I |
|
|
|
|
|
II |
|
|
|
|
III |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U = ∞ |
|
|
|
|
|
|
|
U = ∞ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
б |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13.1 |
|
|
|
|
|||||
может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U = 0 внутри ямы (при 0 £ х £ l) и U = ∞ вне ямы (при х < 0 и х > l).
Рассмотрим стационарное уравнение Шредингера. Поскольку Y-функ- ция зависит только от координаты х, то уравнение имеет вид
d 2ψ/ dx2 +(2m / 2)(E −U )ψ = 0. |
(13.1) |
За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Следовательно, и функция y за пределами ямы равна нулю. Из условия непрерывности следу-
ет, что y должна быть равна нулю и на границах ямы, т. е. |
|
ψ(0) = ψ(l) = 0 . |
(13.2) |
Этому условию должны удовлетворять решения уравнения (13.1). В области II (0 £ х £ l), где U = 0 уравнение (13.1) имеет вид
d2ψ/ dx2 + (2m/ 2)Eψ = 0.
Используя обозначение k2 = 2mE/ 2, придем к известному из теории колебаний волновому уравнению
d2ψ/ dx2 + k2ψ = 0.
Решение такого уравнения имеет вид
ψ(x) = asin(kx+ α). |
(13.3) |
Условию (14.2) можно удовлетворить соответствующим выбором постоянных k и a. Из равенства ψ(0) = 0 получаем ψ(0) = asinα = 0 Þ a = 0.
Далее из равенства ψ(l) = 0 получаем ψ(l) = asin(kl) = 0. Это условие выполняется при
47

kl = ±nπ (n = 1, 2, 3, ...), |
(13.4) |
n = 0 исключено, поскольку при этом ψ º 0, т. е. вероятность обнаружения частицы в яме равна нулю.
Из (13.4) получаем 2mEl2 / 2 = n2π2 (n = 1, 2, 3, ...), следовательно,
En = π2 2n2 /2ml2(n = 1, 2, 3, ...).
Таким образом получаем, что энергия частицы в потенциальной яме может принимать только дискретные значения. На рис.13.1, б изображена схема энергетических уровней частицы в потенциальной яме. На этом примере реализуется общее правило квантовой механики: если частица локализована в ограниченной области пространства, то спектр значений энергии частицы дискретен, при отсутствии локализации спектр энергии непрерывен.
Подставим значения k из условия (13.4) в (13.3) и получим
ψn(x) = asin(nπx/l).
Для нахождения константы а воспользуемся условием нормировки, которое в данном случае имеет вид
l
a2 òsin 2 (nπx / l)dx =1.
0
На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение sin2 (nπx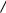 l) (равное, как известно, 1/2) на длину промежутка. Таким образом, получаем a2l / 2 =1 Þ a =
l) (равное, как известно, 1/2) на длину промежутка. Таким образом, получаем a2l / 2 =1 Þ a = 
 2 / l . Окончательно собственные волновые функции имеют вид
2 / l . Окончательно собственные волновые функции имеют вид
ψn(x) = 
 2/l sin(nπx/l) (n = 1, 2, 3, ...).
2/l sin(nπx/l) (n = 1, 2, 3, ...).
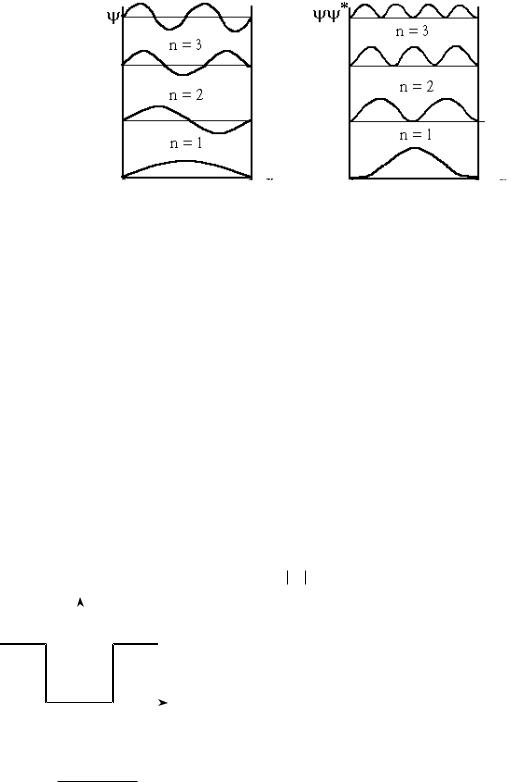
Графики собственных значений функций при различных n изображены на рис. 13.2. На этом же рисунке показана плотность вероятности yy обнаружения частицы на различных расстояниях от стенок ямы.
48
|
|
n = 4 |
|
|
|
n = 4 |
|||||||||
|
|
|
|
|
|
|
|
ψψ* |
|
|
|
|
|
|
|
ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
n = 3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 2 |
||||
|
|
n = 2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 1 |
||||
|
|
n = 1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
x |
0 |
|
|
|
|
l |
x |
|||
|
|
l |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
Рис. 13.2
Графики показывают, что в состоянии с n = 2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, несовместимо с представлением о траектории. Отметим, что, согласно классическим представлениям, все положения частицы в яме равновероятны.
14. ПОТЕНЦИАЛЬНАЯ ЯМА КОНЕЧНОЙ ГЛУБИНЫ
Рассмотрим задачу о движении частицы в потенциальной яме со стенками конечной высоты U0 (рис. 14.1).
Найдем собственные волновые функции ψn и собственные значения энергии En, которые удовлетворяли бы граничному условию: при больших значениях x функция ψ(х) стремится к нулю.
U(x) |
|
|
|
|
|
|
Рассмотрим только правую половину ямы ( x ³ 0). |
|
|
|
|
|
|||||
U0 |
|
|
|
U(x) |
|
|
В области II уравнение Шредингера записыва- |
|
|
|
|
|
I |
II |
|
|
ется в виде |
|
|
|
|
|
|
d2ψ/ dx2 + (2m/ 2)(E −U )ψ = 0. |
||
|
|
|
|
|
|
|
|
|
–x0 0 x0 |
|
x |
||||||
|
Решение этого уравнения имеет вид |
|||||||
|
|
|
|
|
|
|
|
|
Рис. 14.1
ψ2 = a2 exp(−βx) + b2 expβx,
где β = 
 2m(U0 − E)
2m(U0 − E) . При этом в области II (E − U 0 ) < 0. Граничному условию для области II удовлетворяет решение
. При этом в области II (E − U 0 ) < 0. Граничному условию для области II удовлетворяет решение
ψ2 = a2 exp(−βx). |
(14.1) |
В области I уравнение Шредингера записывается в виде
49

d2ψ/dx2 + (2m/ 2)Eψ = 0, |
|
а решения этого уравнения имеют вид (см. разд. 13): |
|
● при нечетных значениях n |
|
ψ1 = a1coskx; |
(14.2) |
● при четных значениях n |
|
ψ1 = a1sinkx, |
(14.3) |
где k2 = 2mE/ 2. |
|
При x =x0 Ψ-функция должна удовлетворять стандартным условиям
ψ1(x0) = ψ2(x0); dψ1(x0)/dx= dψ2(x0)/dx. (14.4)
Для нечетных энергетических уровней, подставляя (14.1) и (14.2) в (14.4), получаем соотношения
|
a coskx =a exp(−βx ) |
; |
|
|
|
||||||||||
1 |
0 |
2 |
0 |
|
|
|
|
||||||||
− a1k sin kx0 = −a2βexp(−βx0 ) . |
|
||||||||||||||
Разделив эти соотношения, получим |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k tg kx0 = β. |
|
|
|
|
|
|||||||
Учитывая, что k 2 = 2mE / 2 |
и β = |
|
|
|
, запишем |
|
|||||||||
2m(U0 − E) |
|
||||||||||||||
k tg |
|
|
|
x0 = |
|
|
|
; |
|
||||||
2mE 2 |
|
||||||||||||||
2m(U0 − E) |
|
||||||||||||||
|
|
|
|
. . |
(14.5) |
||||||||||
tg |
2mE 2 |
x0 = |
|||||||||||||
|
(U0 − E) |
E |
|||||||||||||
Уравнение (14.5) является трансцендентным и может быть решено либо графически, либо методом итераций, либо методом «проб и ошибок». По найденному любым из этих способов собственному значению энергии En (значения положительных корней этого уравнения) можно определить собственные значения Ψ-функции, и соответственно,
βn = 
 2m (U 0 − E n ) / ; kn =
2m (U 0 − E n ) / ; kn = 
 2mEn
2mEn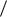 2 .
2 .
Для четных значений n (14.3) запишем граничные условия (14.4) при x =x0:
a1sinkx0 = a2 exp(−βx0);
a1kcoskx0 = −a2βexp(−βx0).
Разделив эти соотношения, получим трансцендентное уравнение, которое позволит определить собственные значения энергии и Ψ-функции на четных энергетических уровнях:
50
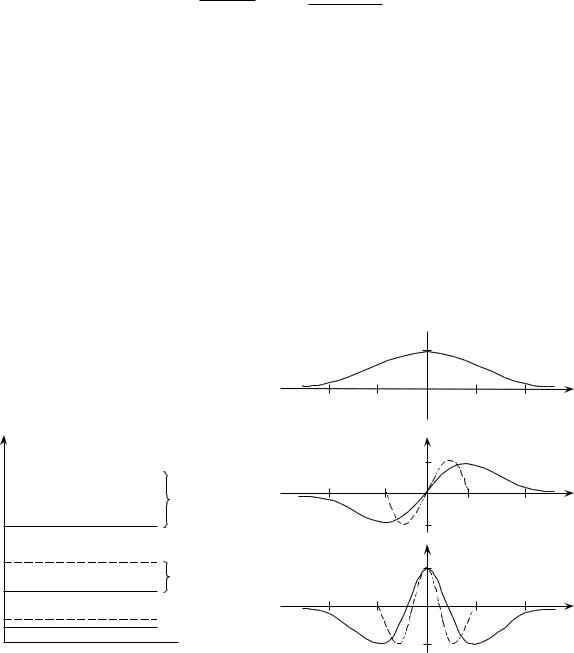
ctg
 2mE
2mE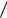 2 x0 = −
2 x0 = −
 (U0 − E)
(U0 − E)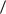 E .
E .
Поскольку тангенс и котангенс периодические функции, частица в потенциальной яме может иметь лишь дискретные уровни энергии. Чем глубже яма, тем больше уровней энергии разрешены для частицы, причем уровни, которым отвечают четные и нечетные волновые функции, чередуются.
На рис. 14.2 показаны уровни энергии, а на рис. 14.3 – волновые функции, соответствующие первым трем энергетическим уровням для ямы конечной глубины (сплошные линии) и в бесконечно глубокой потенциальной яме (штриховые линии).
Е |
Е3 |
Е2 |
Е1 |
0 |
Рис. 14.2 |
ψ 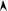
–x0 |
0 |
x0 |
x |
|
ψ2 |
|
|
–x0 |
0 |
x0 |
x |
|
ψ3 |
|
|
–x0 |
0 |
x0 |
x |
Рис. 14.3
В заключение заметим, что общее решение задачи о частице, находящейся в прямоугольной яме конечной глубины, встречается при рассмотрении многих задач атомной физики, например, эмиссии электронов из металлов, радиоактивного распада и т. д.
51
