мире не сможет вам “объяснить” ни на капельку больше того, что “объяснили” мы. Никто не дает вам никакого более глубокого представления о положении вещей. У нас их нет, нет представлений о более фундаментальной механике, из которой можно вывести эти результаты».

11.ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ

Вклассической механике состояние материальной точки определяется заданием значений координат и импульса. Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных при измерениях получаются определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты х и компоненты импульса px . Неопределенности значений х и px удовлетворяют соотношению

Из (11.1) следует, что, чем меньше неопределенность одной из переменных (х или px ), тем больше неопределенность другой. Возможно такое состояние, когда одна из переменных имеет точное значение, а другая переменная при этом оказывается совершенно неопределенной.

Соотношение, аналогичное (11.1), имеет место для у и py, z и pz , а также для ряда других пар величин (такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно написать

Соотношение (11.2) называется принципом неопределенности для величин А и В. Это соотношение сформулировал В. Гейзенберг в 1927 г. Утверждение о том, что произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка, называется принципом неопределенности.

Энергия и время также являются канонически сопряженными величина-

ми

DEDt ³ /2.

Это соотношение означает, что определение энергии с точностью Е должно занять интервал времени, равный по меньшей мере Dt ³ /2DE .

41

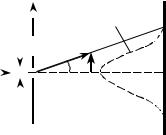
Соотношение неопределенности можно проиллюстрировать следующим примером. Попытаемся определить значение координаты х свободно летящей микрочастицы, поставив на ее пути щель шириной х, расположенную перпендикулярно к направлению движения частицы.

До прохождения частицы через щель ее составляющая импульса px имеет точное значение равное нулю (щель по условию перпендикулярна к

х, но это достигается ценой утраты определенности значения px . Действительно, вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2ϕ, где ϕ – угол, соответствующий первому дифракционному максимуму (максимумами высших порядков можно пренебречь, поскольку их интенсивность мала по сравнению с интенсивностью центрального максимума). Таким образом, появляется неопределенность

px = psinϕ .

Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной х, соответствует угол ϕ, для которого

sinϕ = λ/ x.

Следовательно, px ≈ pλ / x, и получаем

х рх ≈ pλ ≈ /2.

Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив в (11.1)

DxDvx ³ /2m.

Очевидно, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью применимо понятие траектории. Уже для макрочастицы размером 1 мкм

42

неопределенности значений х и vx оказываются за пределами точности измерения этих величин, так что ее движение будет практически неотличимо от движения по траектории.

Принцип неопределенности является одним из фундаментальных положений квантовой механики.

12.УРАВНЕНИЕ ШРЕДИНГЕРА

Вразвитие идеи де-Бройля о волновых свойствах вещества австрийский физик Э. Шредингер получил в 1926 г. уравнение, названное впоследствии его именем. В квантовой механике уравнение Шредингера играет такую же фундаментальную роль, как законы Ньютона в классической механике и уравнения Максвелла в классической теории электромагнетизма. Оно позволяет найти вид волновой функции частиц, движущихся в различных силовых

полях. Вид волновой функции или Ψ-функции получается из решения уравнения, которое выглядит следующим образом

Здесь m – масса частицы; i – мнимая единица; – оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых производных по координатам

ΔΨ=∂2Ψ/∂x2 +∂2Ψ/ ∂у2 +∂2Ψ/ ∂z2.

Буквой U в уравнении (12.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу.

Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других уравнений. Если силовое поле, в котором движется частица, стационарно (т.е. постоянно во времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера состоит из двух множителей, один из которых зависит только от координат, другой – только от времени

43

Здесь Е – полная энергия частицы, которая в случае стационарного поля остается постоянной; ψ(x, y, z) – координатная часть волновой функции. Чтобы убедиться в справедливости (12.2), подставим его в (12.1):

−( 2 /2m)exp(−i(E / )t) ψ+Uψexp(−i(E / )t) =i (−i(E / ))ψexp(−i(E / )t) .

Врезультате получим

Уравнение (12.3) называется уравнением Шредингера для стационарных состояний. В дальнейшем мы будем иметь дело только с этим уравнением и для краткости будем называть его просто уравнением Шредингера. Уравнение (12.3) часто записывают в виде

ψ+(2m/ 2)(E −U )ψ = 0.

В квантовой механике большую роль играет понятие оператора. Под оператором подразумевается правило, посредством которого одной функции, обозначим ее ξ сопоставляется другая функция, обозначим ее f. Символически это записывается следующим образом

f =θξ,

здесь θ – символическое обозначение оператора (можно было взять любую другую букву со «шляпкой» над ней, например A, M и т. д.). В формуле

координатам, х, у, z, с последующим суммированием полученных выражений. Оператор может, в частности, представлять собой умножение исходной

Гамильтона). Гамильтониан является оператором энергии Е. В квантовой механике другим физическим величинам также сопоставляются операторы. Со-

44

ответственно, рассматриваются операторы координат, импульса, момента импульса и т. д. Для каждой физической величины g составляется уравнение, аналогичное (12.4). Оно имеет вид

Qϑ=gϑ,

где Q – оператор, сопоставляемый g. Так, например, оператор импульса определяется соотношениями

px = −i∂/∂x; pу = −i ∂/ ∂у; pz = −i∂ /∂z,

или в векторном виде p=-i Ñ, где Ñ – градиент.

В разд. 10 мы уже обсуждали физический смысл Y-функции: квадрат модуля Y-функции (волновой функции) определяет вероятность dP того,

Поскольку квадрат модуля волновой функции равен произведению волновой функции на комплексно сопряженную величину Ψ2 =ΨΨ , то

dP = ΨAΨ dV .

Тогда вероятность обнаружения частицы в объеме V

P = A òdP = A ò Ψ 2 dV .

VV

Для одномерного случая

x

P= A ò2 Ψ(x ) 2 dx .

x1

Интеграл от выражения (12.5), взятый по всему пространству от − ∞ до + ∞ , равняется единице:

A òΨΨ dV =1

Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т. е. вероятность достоверного события, которая равна 1.

В квантовой механике принимается, что волновая функция допускает умножение на отличное от нуля произвольное комплексное число С, причем Ψ и СY описывают одно и то же состояние частицы. Это позволяет выбрать волновую функцию так, чтобы она удовлетворяла условию

45