
electrodynamics
.pdf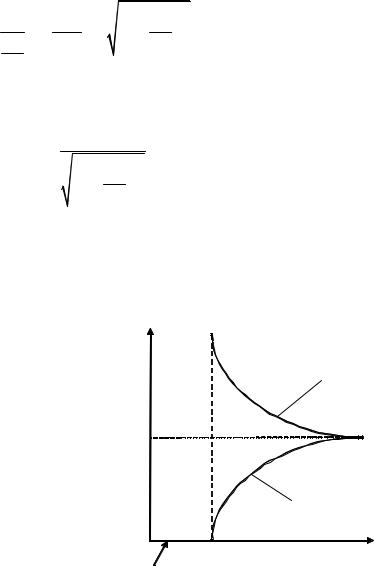
|
|
|
|
vgr = |
1 |
βc2 |
|
|
|
ω |
2 |
|
|||
|
|
|
|
∂β |
= c |
= c |
|
1 − |
c |
. |
(4.17) |
||||
|
|
|
|
|
|
|
ω |
|
|
|
|
ω |
|
||
|
|
|
|
|
|
∂ω |
|
|
|
|
|
|
|
|
|
|
Используя понятие критической частоты, выражение (4.13) для фазо- |
||||||||||||||
вой скорости можно записать как |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
vph = |
|
c |
|
|
. |
|
|
(4.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
ω |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
1 − |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
||
|
Тогда из (4.17) и (4.18) получим |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
v |
v |
|
= c2. |
|
|
(4.19) |
|
|
|
|
|
|
|
|
|
gr |
ph |
|
|
|
|
|
|
|
При понижении частоты фазовая скорость в волноводе растет, а груп- |
||||||||||||||
повая |
– |
падает |
при |
ω → ωc , |
|
|
|
|
|
|
|||||
v |
→∞, |
v |
→ 0 . Это означает, что |
vgr,ver |
|
|
|
||||||||
ph |
|
|
gr |
|
|
|
|
|
|
|
|
|
|
|
|
сигнал в волноводе при ω < ωc |
рас- |
|
|
|
|
|
vph |
||||||||
пространяться не может. |
|
|
|
|
|
|
|
|
|
|
|||||
|
На рис. 4.5 показаны зависимо- |
|
|
c |
|
|
|
||||||||
сти фазовой и групповой скоростей |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
волн в волноводе при вакуумном за- |
|
|
|
|
|
|
|||||||||
полнении от частоты. |
|
|
|
|
|
|
|
|
|
|
vgr |
||||
|
Заметим, что связь между фазо- |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
вой и групповой скоростями, которая |
|
|
|
|
|
ω |
|||||||||
определяется |
соотношением (4.19), |
|
|
|
|
|
ωc |
||||||||
|
|
Область непрозрачности волновода |
|||||||||||||
не универсальна. Она справедлива |
|
|
|||||||||||||
|
Рис. 4.5. Фазовая и групповая скорости |
||||||||||||||
только в частном случае волновода, |
|
волны в волноводе в функции от час- |
|||||||||||||
несущего электромагнитную волну. |
|
|
тоты |
|
|
|
|||||||||
|
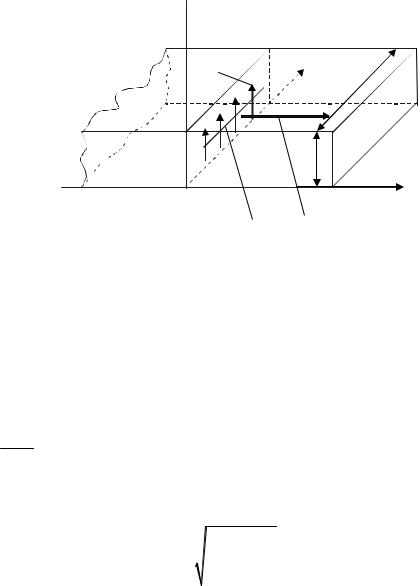
Поток мощности через поперечное сечение волновода. Воспользу- |
||||||||||||||
емся вектором Пойнтинга (рис. 4.6). Согласно теореме Пойнтинга, средний |
|||||||||||||||
по времени поток активной мощности Р, проходящей через поперечное се- |
|||||||||||||||
чение S волновода в направлении его оси, может быть вычислен из соот- |
|||||||||||||||
ношения |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a b r |
r |
|
|
||
|
|
|
|
|
|
|
|
P = ∫ ∫ |
ΠdS , |
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
63
|
|
r |
1 |
|
r |
r |
|
r |
|
|
где |
Π – вектор Пойнтинга |
( Π = |
Re E |
H |
* ); |
H |
* |
– комплексно- |
||
|
m |
|||||||||
|
|
|
|
|
m |
|
m |
|
|
|
2
сопряженная амплитуда вектора напряженности магнитного поля.
y 
x
a
b
z
H Π
Рис. 4.6. Вектор Пойнтинга в прямоугольном волноводе с основным типом поля.
Для основного типа поля имеем:
|
|
|
|
π |
|
−iβz |
|
E |
π |
|
−iβz |
|
||||
Ey = Em sin |
|
|
|
x e |
|
|
; H x = − |
m |
sin |
|
x e |
|
; |
|||
|
|
|
|
Z g |
|
|
||||||||||
|
|
|
|
a |
|
|
|
|
a |
|
|
|
||||
r |
r |
E |
2 |
|
sin2 |
π |
|
|
|
|
|
|
|
|||
Π(x) = e |
z |
m |
|
x. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
2Z g |
|
a |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Z g = ωµ0 – волновое сопротивление волновода.
β
Тогда из (4.10) и (4.11) следует, что
Z g = |
|
120π |
|
|
. |
(4.20) |
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
|
λ |
2 |
|
||
|
1 − |
|
|
|
|||
|
|
|
|||||
|
|
|
λc |
|
|||
Вычислив интеграл от вектора Пойнтинга по поперечному сечению волновода, получим поток мощности вдоль оси волновода:
a b |
E |
2 |
sin2 |
π |
|
E 2 |
|
ab |
|
|||
P = ∫ ∫ |
|
m |
|
|
x dxdy ; |
P = |
m |
|
|
, |
(4.21) |
|
|
|
|
|
|
||||||||
0 0 |
2Z g |
a |
|
2Z g |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где Em – амплитуда напряженности электрического поля.
64

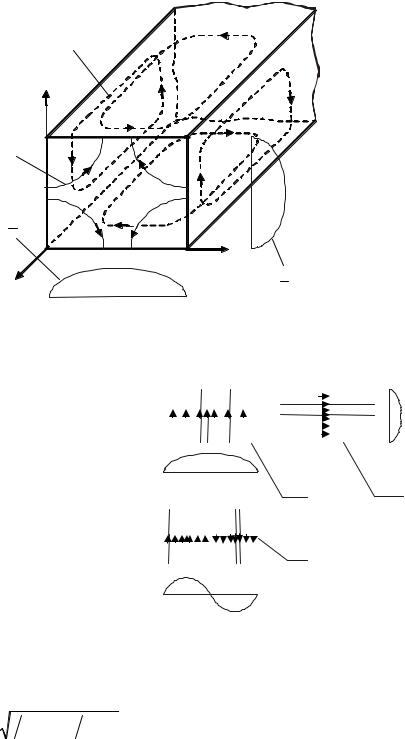
На рис. 4.7 показано распределение векторов напряженности электрического поля, магнитного поля и вектора Пойнтинга в поперечном сечении волновода.
r |
π |
|
|
Ey (x) sin |
x |
||
|
|||
|
a |
||
|
r |
|
π x |
|
Hx(x) sin |
||
|
|
|
a |
0 |
a |
x |
0 |
r |
2 π |
x |
|
|
Π(x) sin |
a |
|
|
|
|
|
|
|
|
a |
x |
0 |
a |
x |
r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.7. Векторы E , H и Π в поперечном сечении волновода в функции координаты |
||||||||||||||||
Преобразуем выражение (4.21). Используя (4.20), получим |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ε |
0 |
E |
2 ab |
1 |
|
|
|
|
λ 2 |
||||||
P = |
|
|
m |
|
|
|
|
1 |
− |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
2 |
|
|
ε0µ0 |
|
λc |
|||||||
С использованием выражения для групповой скорости (4.17) полученное соотношение для потока мощности через поперечное сечение волновода можно переписать так:
|
ε |
0 |
E |
2 |
|
ab |
|
|
P = |
|
|
m |
|
|
vgr . |
(4.22) |
|
|
|
|
|
|
|
|||
22
Соотношение (4.22) можно интерпретировать следующим образом:
• при распространении волны объемная плотность энергии электромаг- нитного поля переносится через поперечное сечение волновода с группо-
вой скоростью. В случае, когда vgr → 0 , перенос энергии по волноводу
прекращается.
Если изменить знак у β , то изменятся знаки у vph и vgr , а также на-
правление вектора Пойнтинга. Таким образом, если изменить направление распространения волны в смысле направления движения поверхности постоянной фазы, то изменится и направление потока мощности.
65
4.2. Высшие типы поля в прямоугольном волноводе
Классификация типов поля прямоугольного волновода. Основным признаком типа поля принято считать наличие силовых линий поля, имеющих продольную компоненту. Рассмотренные в 4.1 решения уравнений Максвелла имеют продольную компоненту H , поэтому их принято назы-
вать волнами магнитного типа, или волнами H-типа. Для обозначения ти-
па поля берется в расчет число полуволн изменения полей на поперечном сечении вдоль оси х и оси у. Волна, описываемая решением
Ay = A0 sin nπ x e−iβx ,
a
содержит n полуволн вдоль оси х. В общем случае вводится символ Hnm , который означает, что в рассматриваемой волне имеется продольная компонента магнитного поля (при этомEz = 0 ; по оси х – укладывается n полуволн, по оси y укладывается m полуволн). Рассмотренный в 4.1 простейший тип поля прямоугольного волновода обозначался символом H10 .
В волноводе также возможны волны, у которых продольная компонента электрического поля Ez отлична от нуля, тогда как продольная компонента магнитного поля равна нулю ( H z = 0 ). Такие типы поля обозначают символом Enm . Этот символ означает, что в рассматриваемой волне имеется продольная компонента электрического поля, по оси х укладывается n полуволн, по оси y укладывается m полуволн.
Волны Е-типа называют продольно-электрическими волнами; их так-
же называют волнами ТМ-типа, или поперечно-магнитными волнами. |
||
y |
Аналогично, волны Н-типа называют про- |
|
дольно-магнитными волнами; их также на- |
||
|
||
b |
зывают волнами ТЕ-типа, или поперечно- |
|
|
электрическими волнами. |
|
|
|
Волны электрического типа в пря- |
||
|
a |
моугольном |
волноводе |
(Emn -волны, или |
0 |
x |
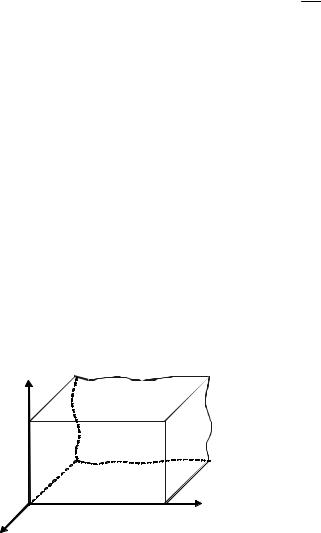
На рис. 4.8 |
показаны система |
|
z |
|
ТМ-волны). |
||
|
координат и размеры поперечного сечения |
|||
Рис. 4.8. Система координат |
||||
и размеры волновода |
|
прямоугольного волновода. |
||
66
Нужно найти такое решение уравнений Максвелла, при котором H z = 0 , что по определению соответствует Е-типу волн. Данное решение можно сформировать с помощью векторного потенциала. Известно, что
H= rot A; E = −iωµ0 A − grad ϕ; div A = −iωε0ϕ.
Впустом волноводе ток проводимости отсутствует ( j = 0 ). Исключим
φ, тогда
|
r |
|
r |
r |
1 |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|||||
|
H = rot A; E = |
|
(ω2ε0µ0 A + grad div A). |
|
(4.23) |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
iωε0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• Если выбрать |
векторный потенциал A таким, |
что он имеет |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
только продольную компоненту |
|
A = ez A( x, y, z ), то |
|
|
Hz |
= 0 |
благодаря |
|||||||||||||||||||||||
свойствам операции rot . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Действительно, из (4.23) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
H x |
|
= |
|
∂A |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
H y |
= − |
∂A |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
H z = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= |
|
1 |
|
|
∂2 A |
|
|
|
|
|
|
|
|
|
|
(4.24) |
|||||||
|
|
|
|
|
Ex |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
iωε0 ∂x∂z |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
= |
|
1 |
|
|
∂2 A |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Ey |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
iωε0 ∂y∂z |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ω2ε µ |
|
|
∂ |
2 |
A |
|
|
|
|||||||||
|
|
|
|
|
E |
|
= |
|
|
|
|
A + |
|
|
. |
|
|
|||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
∂z |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
iωε0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Дифференциальное уравнение для A известно – это волновое уравне- |
||||||||||||||||||||||||||||||
ние: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 A( x, y, z ) |
+ |
∂2 A(x, y, z ) |
+ |
|
∂2 A( x, y, z ) |
+ ω2ε µ |
|
|
A( x, y, z ) = 0 . (4.25) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
∂x2 |
|
|
∂y2 |
|
|
|
|
|
|
|
|
|
∂z2 |
|
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим граничные условия. Нужно найти решения в виде бегу- |
||||||||||||||||||||||||||||||
щей вдоль волновода волны, поэтому |
A( x, y, z ) = f ( x, y )e−iβz . |
Тогда вы- |
||||||||||||||||||||||||||||
бранный вектор A пропорционален продольной компоненте электрического поля Ez . Ez касательна стенкам и поэтому на них равна нулю, т. е.
67

f (x, y) x=0,a = f (x, y) x=0,b = 0 .
Решение волнового уравнения при таких граничных условиях имеет
вид
A( x, y, z ) = A |
sin |
nπx |
|
sin |
mπy |
e−iβz . |
(4.26) |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
nm |
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Граничные условия выполняются при n = 1, 2, 3...; m = 1, 2, 3. Подста- |
|||||||||||||||||||||||||
вим решение (4.26) в (4.25). Получим дисперсионное уравнение |
|
||||||||||||||||||||||||
β2 = ω2ε0µ0 |
|
|
|
nπ 2 |
|
|
mπ |
2 |
|
||||||||||||||||
|
− |
|
|
|
|
|
− |
|
|
|
|
|
(4.27) |
||||||||||||
|
|
|
|
|
b |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π 2 |
|
2π 2 |
2π |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
− |
|
|
|
|
|
, |
(4.28) |
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
λ |
|
|
|
|
λc |
|
|
|
||||||||||||
|
λ g |
|
|
|
|
|
|
|
|||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
n |
2 |
|
|
|
m 2 |
|
|
|
|||||||||||||
|
|
|
= |
|
|
|
|
|
|
+ |
|
|
|
. |
|
|
(4.29) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
λc |
2a |
|
|
|
|
2b |
|
|
|
|
|
||||||||||||||
Чем больше значения n и m, тем меньше критическая длина волны λc . Подставим найденное решение (4.26) в (4.24). Получим:
H x = Anm |
|
|
mπ |
nπx |
|
mπy |
|
−iβz |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
sin |
|
|
|
|
|
cos |
|
|
|
|
e |
|
|
|
|
|
|
; |
|
|
|
|
|
|||||||||||
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
H y = Anm |
|
nπ |
|
|
|
|
nπx |
|
mπy |
−iβz |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
cos |
|
|
|
|
|
sin |
|
|
|
|
e |
|
|
|
|
|
|
; |
|
|
|
|
|
|||||||||||||
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
H z = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(E) nπ |
|
|
|
nπx |
mπy |
|
|
−iβz |
|
|
|
|
|||||||||||||||||||||||||
Ex = − AnmZ g |
|
|
|
|
cos |
|
|
|
sin |
|
|
|
|
|
|
e |
|
|
|
|
|
; |
|
|
|||||||||||||||
|
|
a |
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
(E) mπ |
|
|
|
nπx |
mπy |
|
−iβz |
|
|
|
|||||||||||||||||||||||||||
Ey = − AnmZ g |
|
|
|
|
|
sin |
|
|
|
cos |
|
|
|
|
|
e |
|
|
|
|
|
; |
|
|
|||||||||||||||
|
|
|
b |
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
nπ |
2 |
|
|
mπ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
+ |
|
|
|
|
|
|
nπx |
|
mπy |
−iβz |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
(E) a |
|
|
|
|
b |
|
|
|
|
||||||||||||||||||||||||||||||
Ez = iAnmZ g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
sin |
|
|
|
|
|
|
e |
|
, |
|||||||||||
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|||||||||||||||
где Z g(E) – это волновое сопротивление волновода в случае волны Е-типа:
68
Z g(E) = Ez 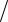 H y = Ey
H y = Ey  H x .
H x .
Из (4.24) следует, что
Z g(E) = β .
ωε0
Заметим, что из (4.27) – (4.29) следует, что β = ω
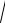 ε0µ0
ε0µ0 
 1 − (λ
1 − (λ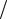 λc )2 ,
λc )2 ,
|
|
µ0 |
|
|
|
|
|
|
тогда Z |
(E) = |
|
1 − (λ λ |
c |
)2 . |
|||
|
||||||||
|
g |
ε0 |
|
|
||||
|
|
|
|
|
||||
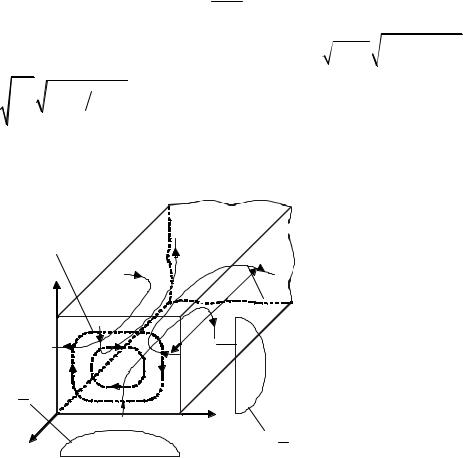
На рис. 4.9 показаны силовые линии электрического и магнитного полей волны типа Е11 (n = 1, m = 1).
r |
|
|
|
H |
|
|
|
y |
|
|
|
b |
|
r |
|
|
E |
|
|
|
|
λ g |
|
|
|
2 |
|
sin π x |
|
|
|
a |
|
x |
|
0 |
a |
π y |
|
z |
|
sin |
|
|
|
b |
|
|
|
|
Рис. 4.9. Силовые линии электрического и магнитного полей типа поля E11 в прямоугольном волноводе
Волны магнитного типа в прямоугольном волноводе ( Hnm -волны,
или TEnm -волны). Для получения решения вводят симметричный вектор-
ный потенциал A → A' , соответствующий замене ε0 на −µ0 . Для волны
Enm : |
r |
|
|
|
|
|
|
|
|
r |
A(x, y, z ); |
|
|
||||
|
A = e |
z |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
r |
|
|
1 |
|
|
||
E |
E = |
|
|
|
|
(ω2ε µ |
A + grad div A); |
|
|
|
|
|
|||||
nm |
|
iωε0 |
0 0 |
|
|
|||
|
r |
|
|
r |
|
|
|
|
|
H = rot A. |
|
|
|||||
69

Тогда для волны Hnm :
|
|
|
|
r |
|
|
|
|
|
|
r |
|
A'(x, y, z ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
A' = e |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
r |
|||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
H |
|
|
H = |
|
|
|
|
|
|
|
|
|
(ω2ε µ |
A'+ grad div A'); |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
nm |
|
|
|
|
|
|
|
iωµ0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
E = rot A'. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
В этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ex = |
|
∂A' |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ey = |
∂A' |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Ez = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= − |
|
|
|
1 |
|
|
|
|
|
∂2 A' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
H x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
iωµ0 ∂x∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
= − |
|
|
1 |
|
|
|
|
∂2 A' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
H y |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iωµ0 ∂y∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 |
A' |
|
|
|
|
|
||||||
|
|
|
H |
|
= − |
|
|
|
|
|
|
|
ω2ε µ |
|
|
A'+ |
|
. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
iωµ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A'(x,y,z) удовлетворяет |
|
|
|
такому же |
волновому уравнению, что и |
|||||||||||||||||||||||||||||||||||||||||||||||
A(x,y,z). Граничные условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ex |
= |
∂A' |
|
|
y=0,b = 0; Ey = |
∂A' |
|
|
|
y=0,a = 0. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение волнового уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
mπy |
|
|
−iβz |
|
|
|
||||||||||||||||||||||||
|
A' = A'nm cos |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
e |
|
|
|
; |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
β2 = ω2ε0µ0 |
|
|
|
nπ 2 |
|
|
mπ 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Далее проводят действия, аналогичные для случая Е-волны, с той |
||||||||||||||||||||||||||||||||||||||||||||||||||||
лишь разницей, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ey |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Z |
(H ) |
= |
Ex |
|
|
= |
|
= |
µ0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
. |
||||||||||||||||||||||||||
g |
|
H y |
|
|
H x |
|
|
|
|
ε0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 − (λ λc ) |
2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
70
Квантовые числа для Н-волны могут начинаться от нуля (n = 0, 1, 2,..; m = 0, 1, 2,…). Решение уравнений Максвелла для случая n = 1, m = 0 волны H10 подробно разобрано в 4.1. На рис. 4.10 показаны электрические и магнитные силовые линии для волны типаH11 .
|
|
r |
|
|
|
|
H |
|
|
|
y |
|
|
|
r |
b |
|
|
|
E |
|
|
|
|
sin π x |
|
|
|
|
a |
|
|
|
|
|
0 |
a |
x |
|
z |
|
|
sin |
π y |
|
|
|
|
b |
Рис. 4.10. Силовые линии электрического и магнитного полей типа Н11 в прямоугольном волноводе
В |
|
этом |
|
случае |
продольная |
|
компонента магнитного поля |
||||||||||||||||||||||
H z cos |
π |
x cos |
π |
|
y |
касательна |
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
стенкам волновода и максимальна на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
них. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H10 |
H01 |
|
Пример вычисления критической дли- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ны волны различных типов поля. Найти λc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
высших |
типов, |
ближайших |
к основному |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H20 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
типу поля, при а = 23 мм, b = 10 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Основной тип поля: H10 , для него λc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= = 2а = 4,6 см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Соседний магнитный тип поля: |
|
H01; |
|
Рис. 4.11. Сопоставление распреде- |
|||||||||||||||||||||||||
для него λc = 2b = 2,0 см. |
|
|
|
|
|
ления силовых линий электрического |
|||||||||||||||||||||||
|
|
|
|
|
поля для волн H10 , H01 , H20 |
|
|||||||||||||||||||||||
Другие типы поля: |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
H11 и E11: λc = |
|
|
|
1 |
|
= 1,83 |
см; |
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
1 (2a )2 +1 (2b)2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
71
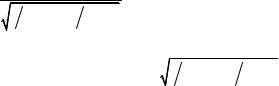
H20: λc = а = 2,3 см;
1
H21 и E21: λc = = 1,52 см; 1 (2a )2 +1 (2b)2
H12 и E12: λc = |
1 |
|
= 0,96 |
см. |
||
|
|
|
||||
|
|
|
||||
1 (2a )2 +1 (2b)2 |
||||||
|
|
|
|
|||
На рис. 4.11 показаны силовые линии электрического поля для трех вариантов волны Н-типа.
4.3.Основной тип поля в круглом волноводе
Вволноводе, образованном трубой в форме круглого цилиндра, также могут распространяться электромагнитные волны. Решение уравнений Максвелла в этом случае потребует использования цилиндрических координат ϕ, r, z и получается в виде комбинаций синусов или косинусов и
функций Бесселя. На рис. 4.12 приведено распределение полей в поперечном сечении круглого волновода с волной H11.
Принятое обозначение H11 соответствует тому, что волна имеет продольную компоненту магнитного поля, одну вариацию по углу ϕ и одну вариацию по радиусу r. Критическая длина волны типа H11 определяется диаметром трубы d:
λc = 1,71d .
Критическую длину волны типа H11 в круглом волноводе можно сопоставить с критической длиной волны типа Н10 в прямоугольном волноводе: λc = 2a .
При d = а средняя ширина круглой трубы несколько меньше ширины прямоугольного волновода. Это обусловливает некоторое уменьшение критической длины волны круглого волновода по сравнению с таковой прямоугольного волновода при d = а.
Конфигурация силовых линий E и H в круглом волноводе с волной H11 и конфигурация силовых линий E и H в прямоугольном с волной H01 топологически подобны. Эти типы поля легко переходят один в другой при плавном трансформировании поперечного сечения прямоугольно-
72
