
electrodynamics
.pdf
линии – это сопротивление единицы ее длины. Рассмотрим поверхностный слой нижнего проводника толщиной t полосковой линии передачи длиной l и шириной w (рис. 5.15).
При условии, что плотность тока не зависит от поперечной координа-
ты, для падения напряжения вдоль продольной оси линии U z |
и тока I в |
||||||||||||
линии справедливо: U z = Ezl, |
I = H xw. |
|
|
|
|
|
|
||||||
Обозначим через R(l) сопротивление отрезка линии длиной l. Реша- |
|||||||||||||
ется квазистатическая задача, поэтому l << λ . В таком случае |
|
||||||||||||
|
|
U |
|
|
Ezl |
|
|
|
l |
|
|||
|
R(l) = |
|
|
= |
|
= Rsur |
|
. |
|
||||
|
I |
H xw |
w |
|
|||||||||
Сопротивление единицы длины линии |
|
|
|
|
|
|
|||||||
|
R = |
1 |
R(l) = R |
1 |
. |
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
1 |
|
|
l |
|
|
|
sur w |
|
||||
Поверхностное сопротивление Rsur было определено в 3.2 выражени- |
|||||||||||||
ем (3.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
также случай |
тонкого проводника (пленки) |
толщиной |
||||||||||
t < δск , где δск |
– скиновая глубина проникновения поля (тока) в толщу |
||||||||||||
проводника. Сопротивление тонкой пленки длиной l
R(l) = 1 l .
σ tw
Погонное сопротивление тонкой пленки:
R1 = 1 1 .
σ tw
Итак, погонное сопротивление полоски шириной w при равномерном распределении тока по ширине полоски:
|
|
|
|
|
|
|
|
|
|
1 |
|
ωµ |
0 |
|
|
t > δск ; |
|||
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
||||
w |
|
|
2σ |
(5.23) |
|||||
R = |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 1 |
, |
|
|
t < δск . |
|||
|
|
|
|
|
|
|
|||
|
w σt |
|
|
||||||
|
|
|
|
|
|
|
|||
Сопоставив выражения для поверхностного сопротивление (3.18) и скиновой глубины (3.20), можно переписать (5.23) в следующем виде:
93
|
|
1 1 |
|
, |
t > δск ; |
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
R1 |
w σδск |
|
|
|||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
, |
|
t < δск . |
|||||
|
|
|
|
|
|
|
||||
|
|
|
w σt |
|
|
|||||
Для полосковой линии, образованной достаточно толстыми проводниками, для которых t > δск , в предположении равномерного распределения тока по сечению линии и в пренебрежении полями рассеяния имеем:
• погонное сопротивление одного проводника в составе линии
R = |
1 |
|
ωµ0 |
; |
|
|
|||
1 |
w |
|
2σ |
|
|
|
|||
• погонную индуктивность линии, состоящей из двух проводников;
h L1 = µ0 w .
Тогда
1ωµ0
R1 |
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
|
δск |
|
|
= |
w 2σ |
|
= |
= |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|||||||||
ωL1 |
|
ωµ0 |
h |
|
|
|
2h ωµ0σ 2 h |
|||||||||
|
w |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вполоске jz ( y )
jz ( y )
Восновании
Используя (5.22), найдем для линии передачи, состоящей из двух проводников:
|
π δск |
|
|
||
α1/м = |
|
|
|
+ tg δд |
, |
|
h |
||||
|
λ |
|
|
||
или
a |
= 27,3 |
1 |
|
δск |
+ tg δ |
. |
|
|
|||||
дБ/м |
|
|
|
h |
д |
|
|
|
λ |
|
|||
|
Приведенные оценки справедливы для |
Рис. 5.16. Распределение плотно- |
случая однородного распределения тока в |
сти тока j в поперечном сече- |
поперечном сечении проводников линии |
нии полоска и проводящего ос- |
(см. рис. 5.15). |
нования микрополосковой линии |
На рис. 5.16 схематически показано рас- |
|
пределение плотности тока в поперечном сечении полоска и проводящего основания микрополосковой линии. Из рисунка можно заключить, что поперечное сечение полоска используется не эффективно: ток течет только по части поперечного сечения, и вклад полоска в потери реально больше,
94
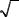
чем это учтено при сделанных ранее оценках. Зато эффективное сечение проводящего основания в данном случае реально больше, чем при условном однородном распределении плотности тока. Это уменьшает вклад в вклад проводящего основания в суммарные потери линии. В результате, сделанная ранее оценка потерь оказывается не такой уж грубой.
Пример:
f |
= 10 ГГц; λ0 = 3 см; δск = 0, 6 мкм; tg δ = 10−3; |
||||||||
h = 0, 3 мм; εд |
= 2; λ = |
3 |
|
2 см |
|||||
|
|
|
|||||||
|
|||||||||
|
|
|
|
|
2 |
|
|
||
a |
|
= |
27, 3 |
(2 10−3 + 10−3 ) = 4,1 дБ/м, или a = 0, 041 дБ/см. |
|||||
дБ/м |
|
||||||||
|
0, 02 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
6.Объемные и планарные резонаторы
Втеории электрических цепей изучаются свойства LCR-коле- бательных контуров, которые используется как основные элементы радиочастотных генераторов или составляющая часть радиочастотных фильтров
вразличных системах передачи и приема радиосигналов. Естественно, что на частотах радиодиапазонов конструктивные элементы LCR-коле- бательных контуров имеют размеры намного меньшие, чем длина волны используемых колебаний. В случае необходимости иметь LCR-коле- бательный контур в СВЧ-диапазоне, сохранив при этом катушку индуктивности и конденсатор как сосредоточенные элементы, их геометрические размеры должны быть много меньше длины волны в окружающей среде. Размеры элементов контура должны не превышать единиц или долей миллиметров. При этом размеры проводников становятся соизмеримыми с глубиной проникновения электромагнитного поля в проводники, а добротность такого колебательного контура становится малой.
Для реализации колебательного контура (резонатора) с достаточно большой добротностью на СВЧ используются отрезки передающих линий, имеющие ограниченную длину и заданные граничные условия на концах такой линии передачи. В качестве указанного резонатора может быть использован отрезок волновода, концы которого закрыты проводящими поверхностями. Таким образом, можно рассмотреть поведение электромагнитного поля в объеме, со всех сторон ограниченном проводящими по-
95
верхностями. Данный конструктивный элемент представляет собой объем- ный резонатор. Можно также использовать отрезки микрополосковой или копланарной линии ограниченной длины с заданными импедансом нагрузок на концах отрезков. В этом случае получают планарные резонаторы, которые находят применение в современной микроэлектронике СВЧ.
6.1. Электромагнитное поле в объемном резонаторе
Рассмотрим отрезок прямоугольного волновода с волной H10 , закороченного металлическими стенками с двух сторон (рис. 6.1).
Составляющие электрического поля в волноводе:
E |
|
= 0; |
E |
|
= 0; |
E |
|
= E sin |
πx |
e−iβz . |
(6.1) |
x |
z |
y |
|
||||||||
|
|
|
|
|
0 |
a |
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решения |
уравнений |
Максвелла |
||||||
|
|
|
|
|
|
|
для прямоугольного волновода удовле- |
||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
творяют граничным условиям на боко- |
|||||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вых стенках волновода: |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ey |
|
x = 0, a = 0. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
прямоугольного |
резонатора |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
добавляется граничное условие на тор- |
|||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цевых стенках |
|
|
Ey |
|
z = 0, c = 0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
z |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Рис. 6.1.Объемный резонатор, образо- |
|
|
|
|
|
(6.2) |
|||||||||||||||||||||||||||
ванный отрезком прямоугольного вол- |
Чтобы удовлетворить |
граничным |
|||||||||||||||||||||||||||||||
новода, закороченного с обеих сторон |
|||||||||||||||||||||||||||||||||
условиям |
(6.2), |
необходимо ввести в |
|||||||||||||||||||||||||||||||
рассмотрение две волны в анализируемом отрезке волновода – отраженную и падающую:
Ey = E0 sin πax (e−iβz + eiβz ).
Положим = −1, тогда
πx
Ey = 2E0 sin a sin βz.
Первая часть условия (6.2) удовлетворяется, так как sin βz = 0 и
Ey z =0 = 0 при z = 0 .
96
Чтобы выполнялось условие
Ey z =c = 0 ,
необходимо положить, чтобы βc = pπ (где p = 1, 2, 3…), отсюда β = pπ c . В задаче появилось третье квантовое число, поэтому электромагнитное поле в объемном резонаторе характеризуется тремя квантовыми чис-
c . В задаче появилось третье квантовое число, поэтому электромагнитное поле в объемном резонаторе характеризуется тремя квантовыми чис-
лами:
•n – число полуволн вдоль оси x;
•m – число полуволн вдоль оси у;
•р – число полуволн вдоль оси z.
E y
x
x x x x x x
x x x
H z
z
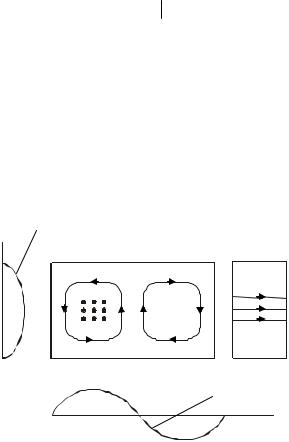
Рис. 6.2. Силовые линии электрического и магнитного полей в прямоугольном резонаторе с типом по-
ля H102
В рассматриваемом частном случае имеем дело с волной Н10 . Пусть р = 2. Тогда
E |
|
= E sin |
πx |
sin |
2πz |
. |
|
|
|
|
(6.3) |
|||||||||
y |
|
|
|
|
|
|
|
|
||||||||||||
|
0 |
|
a |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя уравнения Максвелла, найдем компоненты поля: |
||||||||||||||||||||
H x = − |
E0 |
|
2π |
sin |
πx |
cos |
2πz |
; |
||||||||||||
iωµ0 |
|
|
c |
|
a |
c |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
H y = 0; |
|
|
|
|
|
|
|
|||||||||
|
H z = |
E0 |
|
π |
cos |
πx |
sin |
2πz |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
iωµ0 a |
a |
|
c |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Распределение поля, отвечающее формулам (6.3), показано на рис. 6.2.
97

Врезонаторе существует стоячая волна: компоненты поля H x и H z изменяются во времени синфазно. Напряженность поля Ey по отношению
кH x и H z сдвинута по фазе на 90°.
Вволноводе компоненты Ey и H x совпадают в пространстве, образуя
вектор Пойнтинга. В резонаторе максимумы Ey и H x разнесены, а потому
в резонаторе с идеально проводящими стенками вектор Пойнтинга равен нулю, и переноса энергии в резонаторе нет. В резонаторе электромагнитное поле только запасает энергию.
В общем случае в прямоугольном объемном резонаторе можно выделить волны двух классов – продольно-магнитные Hnmp и продольно-
электрические Enmp . Имеется в виду, что в первом случае продольная
компонента магнитного поля направлена вдоль оси z, а во втором случае вдоль оси z направлена продольная компонента электрического поля.
Представим себе, что в объеме резонатора произошел кратковременный электрический разряд. В резонаторе после окончания разряда возникнут колебания электромагнитного поля на частоте, которая носит название
«собственная частота объемного резонатора». Естественно, что после окончания возбуждающего импульса колебания будут медленно затухать – причём тем медленнее, чем меньше потери энергии в проводящих стенках резонатора.
Найдем собственную частоту прямоугольного объемного резонатора. Возьмем функцию Z, описывающую какой-нибудь вектор поля в объемном резонаторе:
cos |
nπx cos |
nπy cos nπz |
|||||||
Z ( x, y, z ) = Znmp |
|
|
|
|
|
|
|
|
. |
|
|
c |
|||||||
sin |
a sin |
b sin |
|
||||||
В рассматриваемом случае в качестве функции координат в равной мере могут быть использованы как sin, так и cos. Конкретный выбор функции определяется граничными условиями на стенках резонатора. Подставим взятую функцию в волновое уравнение:
Z+ ω2ε0µ0Z = 0,
=∂2 + ∂2 + ∂2 . ∂x2 ∂y2 ∂z2
98
Получим:
|
nπ 2 |
|||
|
− |
|
|
|
a |
||||
|
|
|
||
|
|
|
|
|
− |
mπ |
|
|
2 |
− |
pπ |
|
2 |
+ ω2ε µ |
|
|
|
|
|
|
|
Z (x, y, z) = 0. |
||||||||
|
|
|
|
|
|
|||||||
b |
|
|
|
c |
|
|
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Волновое уравнение имеет ненулевое решение только в том случае, если равно нулю выражение, стоящее в квадратных скобках. Отсюда следует, что
(n,m, p) |
|
|
1 |
|
|
nπ 2 |
|
mπ 2 |
|
pπ 2 |
|
||||||
ω0 |
= |
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
. |
(6.4) |
|
|
|
|
a |
b |
c |
|||||||||||
ε µ |
0 |
||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это и есть собственная частота колебаний объемного резонатора, отвечающая типу колебаний с квантовыми числами n, m, p. Собственная частота колебаний объемного резонатора – его резонансная частота. Если внешнее воздействие (ток) имеет такую же частоту, то в резонаторе возбуждается поле самой большой амплитуды. Эту же формулу можно переписать для собственной частоты резонатора, выраженной в герцах:
(n,m, p) |
|
|
n 2 |
m 2 |
|
p 2 |
||||
f0 |
= c |
|
|
+ |
|
|
+ |
|
|
, |
2a |
2b |
2c |
||||||||
где с – скорость света. |
|
|
|
|
|
|
|
|
|
|
6.2. Добротность объемного резонатора
Добротность объемного резонатора, как и добротность любого колебательного контура, это численная мера отношения запасенной энергии к
энергии, поглощаемой за один период колебаний. Чем |
|
|
|
|||||||||
больше данное отношение, тем больше добротность. |
|
|
|
|||||||||
Для начала |
рассмотрим |
простейшую колебательную |
L |
|||||||||
|
|
|
|
|
|
|
|
|
||||
систему – LCR-контур. |
|
|
|
|
|
|
||||||
|
|
|
|
|
C |
|
|
|||||
|
|
|
|
|
|
|||||||
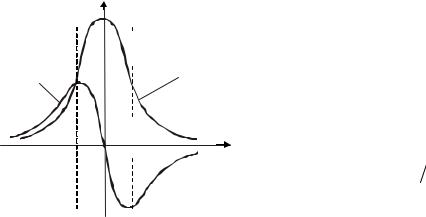
Добротность LCR-контура. Импеданс |
контура |
R |
||||||||||
(рис. 6.3), по отношению к внешней цепи |
|
|
|
|
||||||||
Z = |
|
1 |
|
|
= |
|
iωL + RL |
. (6.5) |
|
|
|
|
|
1 |
|
|
2 |
Рис.6.3. Схема |
|||||||
|
|
|
+ iωC |
1 − ω LC + iωCRL |
|
RCL-колебате- |
||||||
|
|
RL + iωL |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
льного контура |
||||
В случае ωL >> R |
резонансная частота |
контура |
||||||||||
|
|
|
||||||||||
99
ω2 |
= |
1 |
, так что выражение для импеданса (6.5) можно переписать в бо- |
||||||||||||
|
|||||||||||||||
0 |
|
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лее простом виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Z = |
|
|
iωL |
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
ω2 |
|
|
|
|
|
||||
|
|
|
|
|
|
1 − |
|
+ iωCR |
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ω2 |
|
|
L |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
ω2 − ω2 |
2Δω |
|
||||||
|
Вблизи резонанса ωC |
|
, |
0 |
|
|
|
|
|
|
, где Δω = ω − ω0 . Здесь |
||||
|
|
|
|
ω2 |
|
|
|
|
|||||||
|
|
|
|
ωL |
|
|
|
|
ω0 |
|
|||||
Δω – отклонение частоты внешнего источника колебаний от резонансной частоты контура, или, другими словами, – расстройка контура.
|
|
|
|
Импеданс контура вблизи ре- |
|||||
|
|
|
|
зонанса как функция расстройки |
|||||
|
|
|
|
частоты имеет вид |
iωL |
|
|
||
|
|
|
|
|
|
||||
|
|
|
R e Z |
Z = |
|
|
. |
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
Im Z |
|
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
2Δω |
RL |
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
+ i |
|
|
|
|
|
|
|
ω |
|
ωL |
||
|
ω0 |
|
|
Введем обозначение для доб- |
|||||
|
|
|
|||||||
|
|
|
|||||||
|
|
|
|||||||
|
|
ω1 |
ротности контура: |
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
ω |
|
|
ω2 |
|
|
|
|
|
|
1 |
|
|
|
ωL RL = Q , (6.6) |
|||||
|
|
|
|
||||||
|
|
|
|
тогда выражение |
для |
импеданса |
|||
|
|
|
|
контура можно представить так: |
|||||
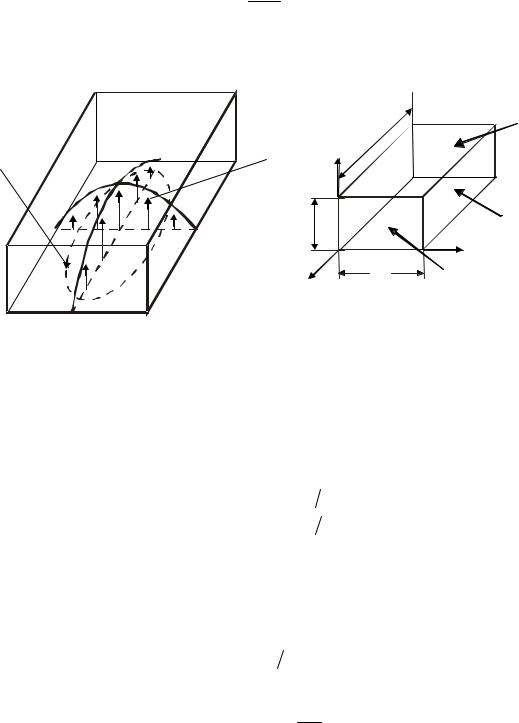
Рис. 6.4. Вещественная и мнимая компоненты импеданса параллельного LCRконтура как функции частоты
Z = Req |
|
1 |
|
. |
|
|
|
||
|
2Δω |
|
||
1 − i |
Q |
|
||
|
|
|||
|
|
ω |
|
|
|
|
0 |
|
|
где Req = RLQ2 – эквивалентное резонансное сопротивление контура.
Теперь можно окончательно выделить вещественную и мнимую части импеданса контура:
1 |
+ i |
|
2Δω |
Q |
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
ω |
|
|
|
|
|
Z = Req |
|
|
|
0 |
|
|
. |
(6.7) |
||
|
|
2Δω |
|
2 |
||||||
1 + |
|
|
|
|||||||
|
|
|
|
|
Q |
|
|
|||
|
ω0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|||
Формула (6.7) иллюстрируется |
рис. |
6.4. Разность |
( ω2 − ω1 = 2Δω ) |
|||||||
принято называть полосой пропускания контура. Характерные точки на рис. 6.4 определяются равенством
100
2Δω
ω0
Q = 1,
в котором ω1 − ω0 = Δω, ω0 − ω2 = Δω.
Добротность LCR-контура Q была определена формулой (6.6).
S1
c
r |
r |
y |
|
H |
E |
||
|
b |
|
S2 |
|
|
x |
z |
a |
S3 |
|
Рис. 6.5. Силовые линии электрического и магнитного полей в прямоугольном резонаторе с типом поля H101 .
Рис. 6.6. Система координат и размеры объемного резонатора к расчету геометрического фактора
Обобщенная формула для добротности. Умножим числитель и зна-
менатель (6.6) на 1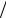 2 Im2 , где Im – амплитуда тока в контуре. Получим
2 Im2 , где Im – амплитуда тока в контуре. Получим
Q = ω |
Im2 |
L 2 |
|
|
|
. |
|
Im2 |
|
||
|
R 2 |
||
Заметим, что LIm2  2 = W , RIm2
2 = W , RIm2  2 = P , где W – максимальная энергия, запасенная в контуре; Р – мощность, поглощаемая в контуре на частоте резонанса.
2 = P , где W – максимальная энергия, запасенная в контуре; Р – мощность, поглощаемая в контуре на частоте резонанса.
Тогда
Q = ωW P , |
(6.8) |
или
Q = 2π PTW ,
где РТ – энергия, поглощенная за один период колебаний тока в контуре.
101
Добротность объемного резонатора. Максимальные энергии, запа-
саемые в резонаторе магнитным полем при H (t) = H m и электрическим полем приE(t) = Em , равны, соответственно,
|
WH |
= ∫ |
µ0Hm2 |
|
dV , |
WE = ∫ |
|
ε0Em2 |
dV . |
||||||||
|
2 |
|
2 |
||||||||||||||
|
|
|
V |
|
|
|
|
|
|
V |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При ω = ω0 WH = WE = W , где W – полная энергия, запасенная в ре- |
|||||||||||||||||
зонаторе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мощность, поглощаемая стенками резонатора: |
|
||||||||||||||||
|
1 |
|
r r * |
|
r |
|
|
|
r |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||||
P = |
|
∫ EτHτ dS, |
|
Eτ |
|
= |
|
Hτ |
|
|
Rsur , |
(6.9) |
|||||
2 |
|||||||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Eτ , Hτ – касательные составляющие векторов электрического и магнитного полей на стенках резонатора; Rsur – поверхностное сопротивление материала стенок.
Исключив из (6.9) Eτ , получим выражение для мощности, поглощаемой в стенках, и в соответствии с (6.8) и (6.9) найдем добротность объемного резонатора:
|
|
|
|
|
ωµ0 ∫ |
|
|
|
r |
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
H |
|
|
|
dV |
|
|
|
||||||||
|
|
|
Q = |
|
|
V |
|
|
|
|
|
|
|
|
|
. |
|
||||
|
|
|
Rsur ∫ |
|
|
|
|
r |
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Hτ |
|
|
|
dS |
|
|
|
|||||||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
||
Учтем, что ωµ0 |
= |
2π |
120π , где λ0 – длина волны в вакууме. Тогда |
||||||||||||||||||
|
|||||||||||||||||||||
|
|
λ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π ∫ |
|
|
r |
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
120π |
|
|
H |
|
|
|
dV |
|
|
|
|||||||
|
|
|
Q = |
V |
|
|
|
|
|
|
|
|
|
|
. |
(6.10) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
||||
|
|
|
|
Rsur λ0 ∫ |
|
|
|
|
2 dS |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
Hτ |
|
|
|||||||||||||
S
Добротность резонатора определяется интегралами от напряженности магнитного поля по объему резонатора и по поверхности стенок, а также поверхностным сопротивлением материала стенок. Из (6.10) следует, что добротность зависит от геометрических размеров резонатора. Принято обозначать:
Q = G Rsur ,
Rsur ,
где G – геометрический фактор, или
102
