electrodynamics

rr

∫Ea Hb dS = uapibp .

S p

Тогда (2.13) может быть переписано в следующем виде:

– от генератора b.

Подставим iap ,iqa ,ibp ,iqb в (2.15). Приведя подобные члены, получим

(uapuqa − ubpuqb )( y pq − yqp ) = 0 .

Поскольку uap ,uqa ,ubp ,uqb могут быть любыми, то y pq − yqp = 0, т. е. Y-матрица симметрична.

В соответствии с данным в начале 2.3 определением рассматриваемая среда взаимна. Или, другими словами, если среда, заполняющая систему,

43

описывается скалярными диэлектрической и магнитной проницаемостями, то Y- и Z-матрицы системы симметричны, т. е. система взаимна.

Если диэлектрическая и магнитная проницаемости материала – скаляры, то материал является изотропным, т. е. его свойства не зависят от направления векторов поля.

Приведенное определение теоремы взаимности несколько сужено. В более полной формулировке теорема взаимности формулируется так:

•если среда, заполняющая систему, описывается симметричными тен- зорами диэлектрической и магнитной проницаемостей, то Y- и Z-матрицы системы симметричны, т. е. система взаимна.

Для упрощения изложения материала здесь не используется тензорное

описание диэлектрической и магнитной проницаемостей среды.

Передатчик Поглотитель

Рис. 2.10. Y-Циркулятор как пример невзаимной цепи. Если антенна недостаточно хорошо согласована, то отраженная от антенны мощность не нарушает работу передатчика, а просто поглощается в нагрузке, что очень важно в радиолокации.

В гл. 7, в которой будут рассмотрены СВЧ-свойства намагниченного феррита, речь пойдёт о тензоре магнитной проницаемости феррита. Этот тензор окажется несимметричным, и, соответственно, СВЧ-устройства, содержащие намагниченный феррит, невзаимными. Действительно, для осуществления невзаимного устройства нужна среда с проницаемостью, описываемой несимметричным тензором. Такой средой служит намагниченный феррит. Забегая вперед, приведем пример невзаимной СВЧ-цепи, которая имеет название «Y-циркулятор». Рис. 2.10 иллюстрирует пример невзаимной цепи с Y-циркулятором, который широко используется в технике СВЧ, в частности для защиты СВЧ-передатчика от волны, отраженной от несогласованной нагрузки.

44

Вернемся к цепям и средам, обладающим взаимностью, т. е. удовлетворяющим условиям реализации теоремы взаимности. Например, любая антенна, не содержащая в своей конструкции намагниченного феррита, имеет одинаковые свойства как в режиме приема, так и в режиме передачи. Поэтому расчет антенн производится, как правило, в режиме передачи, т. е. в режиме излучения волн.

3. ГРАНИЧНЫЕ УСЛОВИЯ, ПОТЕНЦИАЛЫ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ПОЛЕЙ

Устройства или приборы, в которых происходят передача, усиление, преобразование спектра (фильтрация) пакетов электромагнитного поля, сформированы в виде объемов или поверхностей, образованных материалами с различными диэлектрическими, магнитными свойствами или параметрами проводимости. В состав устройства или прибора могут входить объемные элементы, занятые диэлектрическими или магнитными материалами, а также поверхности, образованные проводниками (медь, серебро, золото, сплавы) или сверхпроводниками. Для анализа действия приборов или их проектирования нужно понимать, что происходит с векторами электромагнитного поля на границе объемов или поверхностей, образованных средами с различными диэлектрическими, магнитными или проводниковыми параметрами. Количественная связь между компонентами векторов электромагнитного поля на границе раздела сред с различными свойствами определяется граничными условиями, о которых здесь и пойдет речь.

Далее будут рассмотрены потенциалы электрического и магнитного полей. Из традиционного курса электротехники известно, что напряженность электрического поля E связана с электростатическим потенциалом

ϕ: E = − grad ϕ.

В практической электротехнике широко используется понятие разности потенциалов или электрической напряженности, измеряемых в вольтах. Напряженность электрического поля привлекается к практическому использованию, когда нужно охарактеризовать прочность изоляционных материалов по отношению к электрическому пробою. Для более широкого

45

представления об электромагнитном поле в электродинамике используются как потенциалы, так и напряженности поля. В курсе физики установлено, что потенциал определяет энергию заряженной частицы в электромагнитном поле, напряженность же поля определяет силу, с которой поле действует на частицу. При решении задач электродинамики или техники СВЧ в одних случаях удобнее пользоваться описанием поля с помощью напряженности поля, а в других – с помощью потенциалов. Поэтому важно знать оба способа описания свойств электромагнитного поля, а также переходы от одного способа описания к другому.

3.1. Граничные условия для векторов электрического и магнитного полей

на границе раздела двух сред

Граничные условия для вектора электрической индукции. Рассмот-

рим границу раздела двух сред с различными диэлектрическими проницаемостями ε1 и ε2 . Выделим на границе элементарный цилиндр (рис.

3.1).

Согласно теореме Гаусса–Остроградского, поток вектора электрической индукции D через замкнутую поверхность S равен алгебраической сумме зарядов внутри объема V, ограниченного этой поверхностью:

SV

Устремим высоту цилиндра к нулю (δ → 0) . Тогда (3.1) преобразуется

так:

где D1,n , D2,n – компоненты вектора индукции, перпендикулярные грани-

це раздела; S – площадь основания цилиндра.

Введем поверхностную плотность заряда: lim ρδ = ρsur .

δ→0

Единица измерения поверхностной плотности заряда ρsur – кулон на квадратный метр (Кл/м2).

Тогда (3.2) можно переписать в виде

46

L S

где L – выбранный контур; L = 2 (1 + δ ); S – площадь поверхности, ограниченная контуром L.

Устремим ширину контура δ к нулю, тогда поток вектора B через поверхность S обратится в нуль, а значит получим

47

•на границе раздела двух сред разность касательных составляющих на- пряженности магнитного поля равна поверхностной плотности тока.

48

При отсутствии поверхностного тока

H1,τ = H2,τ.

Это равенство равносильно следующему утверждению:

•на границе раздела двух сред, по которой поверхностный ток не течет, касательная составляющая магнитного поля непрерывна.

Граничные условия на поверхности идеального проводника. Опре-

делим идеальный проводник как проводник, внутрь которого не может проникать электромагнитное поле (Ein = 0, Hin = 0) . Для полей СВЧ-диапазона хорошие проводники (серебро, медь) можно в первом приближении рассматривать как идеальные. На поверхности такого проводника, тем не менее, может течь ток проводимости и формироваться поверхностный заряд. Поэтому на поверхности идеального проводника Eτ = 0 ,

Dn = ρsur , Bn = 0 , H τ = jsur .

Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника (рис. 3.3).

3.2. Поверхностное сопротивление металла по отношению к электромагнитному полю

Рассмотрим случай, когда электромагнитная волна падает на поверхность, образованную неидеальным металлом. Проводимость металла велика, но не бесконечна. Волна может проникать в металл на небольшую глубину и в нём быстро затухает. Ставится задача определить граничные условия для волны со стороны свободного пространства (вакуума).

На рис. 3.4 показана граница раздела «металл – вакуум». Граничные условия для касательных составляющих векторов напряженности электрического и магнитного полей: E1,τ = E2,τ и H1,τ = H2,τ .

На поверхности металла со стороны вакуума отношение касательных компонентов E - и H -полей называется поверхностным импедансом про- водника и выражается формулой Zsur = Eτ1 Hτ1. Со стороны металла отношение касательных составляющих Е- и Н-полей дает волновое сопротивление металлической среды:

49

Eτ2 H τ2 = Z0met .

Сучётом непрерывности касательных составляющих электрического

имагнитного полей на границе раздела получимZsur = Z0met .

Напомним, что для вакуума волновое сопротивление Z0 = µ0 ε0 . Заменой ε0 на εef получим для металла:

Таким образом, поверхностный импеданс металла

Используя 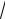i = 1 + i , получим выражения для активной и реактивной

2

составляющих поверхностного импеданса проводника:

Аналогично найдем волновое число волны в металле:

50

где

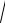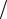δск = 2ωµ0σ.

Декремент затухания волны в металле α определяется найденным параметром δск :

α = 1 δск .

На глубине l = δск амплитуды напряженности поля затухают в е раз.

Параметр δск принято называть «скиновая глубина», или «глубина проник- новения волны в металл». Для меди при f = 10 ГГц и 300 К δск = 0.6 мкм.

Поверхностное сопротивление для меди при тех же условиях в соответствии с формулой (3.4) Rsur = 0,025 Ом.

3.3. Потенциалы электромагнитного поля

Напомним, что в теории статических полей вводятся вспомогательные функции – скалярный потенциал электрического поля ϕ и векторный по-

тенциал магнитного поля A – таким образом, что

В электродинамике для описания электромагнитных полей тоже вводятся скалярный ϕ и векторный A электродинамические потенциалы. Введение потенциалов электромагнитного поля позволяет значительно облегчить решение ряда задач электродинамики. В начале этой главы уже упоминалось о том, что потенциалы определяют энергию заряженной частицы в электромагнитном поле, а напряженность поля определяет силу, с которой поле действует на частицу. Сила, которая действует на частицу, движущуюся в электрическом и в магнитном полях, определяется формулой

F = q(E + [v B]) ,

где q – заряд частицы, v – её скорость.

Эта формула носит название формулы Лоренца. Она широко используется при динамическом расчете движения заряженных частиц (электро-

51

нов или ионов) в электрическом и в магнитном полях. При решении задач квантовой механики силы, действующие на частицы, как правило, в расчет не принимаются. Для расчета квантовых состояний частиц в электрическом и в магнитном полях в соответствующие уравнения вводятся скалярный ϕ и векторный A электродинамические потенциалы, которые определяют энергию частиц в соответствующих квантовых состояниях.

Роль, которую играют потенциалы ϕ и A в электродинамике и квантовой механике, хорошо описана в уже упомянутых «Фейнмановских лекциях по физике» (см. Т. 6 «Электродинамика» и Т. 9 «Квантовая механика» М.: Мир, 1966; 1967.).

Рассмотрим, как потенциалы ϕ и A связаны с векторами напряженности электрического и магнитного полей, и найдем уравнения, которым удовлетворяют указанные потенциалы. Для этого будем использовать уравнения Максвелла.

Зададим векторный потенциал A так, как это делается для статических полей (3.6). Подстановка (3.6) в уравнение Максвелла:

С использованием тождества векторной алгебры rot grad a ≡ 0 функцию, стоящую в (3.7) в скобках, можно приравнять градиенту некоторого скаляра:

Разумно предположить, что этот скаляр есть скалярный потенциал электрического поля. Тогда в статическом случае, когда производная по времени равна нулю, соотношение (3.8) превращается в уже принятое соотношение (3.5).

Итак, получено выражение для напряженности электрического поля, изменяющегося во времени:

52