
electrodynamics
.pdfВектор Пойнтинга перпендикулярен плоскости, в которой лежат векторы E и H . Направление вектора Пойнтинга совпадает с направлением переноса энергии электромагнитной волной.
•Модуль вектора Пойнтинга равен потоку энергии, переносимому элек-
тромагнитной волной в единицу времени через единичную площадку, пер- пендикулярную направлению потока. Или, другими словами:
•вектор Пойнтинга представляет собой плотность потока энергии,
переносимой электромагнитным полем.
Таким образом, выражение (2.5) представляет собой локальное уравнение баланса энергии, справедливое в данной точке пространства в данный момент времени.
Проинтегрируем (2.5) по объему V и используем теорему Гаусса– Остроградского ( ∫ div MdV = ∫ MdS ). Получим
V S
|
|
|
|
|
ur |
|
|
∂ |
|
|
|
|
ε0εr |
|
r |
|
2 |
|
µ0µr |
|
r |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
E |
|
|
|
|
H |
|
|
|
|
|
r r |
|
|||||||
|
|
|
|
|
∫ ΠdS = − |
|
|
∫ |
|
|
|
|
|
|
+ |
|
|
|
|
|
dV − |
∫ |
j EdV . |
(2.6) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
S |
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|||||
Слагаемые в правой части (2.6) представляют собой |
|
|
|
||||||||||||||||||||||||||||
|
∂ |
|
|
r |
|
2 |
|
µ0µr |
|
r |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ε0εr |
E |
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
∫ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
dV – |
скорость изменения энергии, |
запа- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
∂t |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сенной электрическим и магнитным полями в объеме V; |
|
|
|
|
|||||||||||||||||||||||||||
|
∫ |
jEdV |
– энергию, которая выделяется (или поглощается) в объеме за |
||||||||||||||||||||||||||||
V
единицу времени за счет протекания тока;
∫ ΠdS – поток энергии, переносимой электромагнитным полем за
S
единицу времени через поверхность S.
В соответствии с формулами (2.3) и (2.4) соотношение (2.6) можно переписать так:
|
∂ |
|
ur r |
r r |
|
|
− |
(WE total + WH total ) = ∫ |
ΠdS + ∫ jEdV . |
(2.7) |
|||
∂t |
||||||
|
S |
V |
|
|
||
|
|
|
|
|||
33

Выражение (2.7) – математическая запись теоремы Пойнтинга – закона сохранения энергии для электромагнитного поля. Теорема Пойнтинга формулируется следующим образом:
•скорость изменения электромагнитной энергии, запасенной в объеме, равна сумме потока мощности через поверхность, ограничивающую этот объем, и мощности, поглощаемой или выделяемой протекающими
в объеме токами.
Вектор Пойнтинга показывает, насколько внутренние процессы в объеме неуравновешены: при ∫ ΠdS > 0 энергия вытекает из объема V; при
S
∫ ΠdS < 0 энергия поступает в объем V извне.
S
Теорема Пойнтинга в комплексной форме (баланс энергии при гар-
монических колебаниях). Техника высоких частот использует быстрые гармонические колебания, поэтому мгновенные значения энергии практически неинтересны – нужны усредненные во времени энергетические характеристики.
Напомним из курса ТОЭ выражение для мощности в комплексной форме записи. Пусть ток и разность потенциалов имеют следующие физические описания и представления:
I (t) = Im cos ωt , или I (t) = Imeiωt ; U (t) = Um cos(ωt − ϕ) , или
U (t) = Umei(ωt −ϕ).
Мощность, переносимая током при заданной разности потенциалов:
1
I (t)U (t) = ImUm 2 [cos ϕ + cos(2ωt − ϕ)].
Первое слагаемое, содержащее cos ϕ , равно усредненному за период колебаний значению мощности:
|
1 |
T |
1 |
|
|
P = |
∫ I (t)U (t)dt = |
ImUm cos ϕ. |
|||
T |
2 |
||||
|
0 |
|
|||
|
|
|
|
Второе слагаемое – колеблющаяся с удвоенной частотой реактивная мощность: ImUm cos 2ωt .
Проведем усреднение гармонических колебаний U и I:
34

UI = 1 Re(UmIm* ) = 1 Re(Um* Im ) |
|
2 |
2 |
где Um – комплексная амплитуда гармонического колебания: «*» – знак комплексного сопряженная. Для векторных величин:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ur |
2 = |
|
1 |
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
E |
|
E |
|
|
E* |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
m |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
uruu |
|
1 |
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
1 |
|
r |
|
r |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
E H = |
Re(E H |
* ) = |
|
Re(E* |
H |
|
) . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
m |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
m |
|
|
|
m |
|
|
2 |
|
m |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда среднюю мощность P = |
|
|
∫ I (t)U (t)dt можно записать как |
||||||||||||||||||||||||||||||||||
T |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P = |
1 |
Re(I U |
* ) = |
1 |
|
I |
m |
|
|
U |
m |
|
Re eiϕ = |
1 |
|
|
I |
m |
|
U |
m |
|
cos ϕ . |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
m |
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Перейдем теперь к теореме Пойнтинга для гармонических колебаний. Взяв уравнения Максвелла в комплексной форме, произведем над ни-
ми следующие операции:
1. Произведем комплексное сопряжение над вторым уравнением.
r
2. Умножим скалярно первое уравнение на Hm* , второе на Em :
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
rot E |
|
= −iωµ µ |
H |
m |
умножим на H * |
, |
|
|
|
|
|
|
|
|
|
|||||||
m |
|
0 |
|
r |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||
r |
|
|
|
|
|
r |
|
|
r |
|
умножим на E . |
|
|
|
|
|
|
|
|
|||
rot H |
* |
= −iωε |
ε |
E* |
+ j* |
|
|
|
|
|
|
|
|
|
||||||||
|
m |
|
0 |
|
k |
m |
|
m |
|
|
m |
|
|
|
|
|
|
|
|
|
||
3. Вычтем первое уравнение из второго: |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
r |
|
r |
|
|
|
r |
|
r |
|
r |
r |
|
|
r |
|
r |
|
r |
r |
|
|
|
E |
rot H * |
− H * |
rot E = −iωε |
ε |
E* |
E |
+ iωµ |
µ |
H |
m |
H |
* |
+ j |
* E . |
||||||
|
|
m |
|
|
m m |
|
0 |
|
k m m |
0 |
r |
|
|
m m m |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.8) |
4. Используя векторное тождество (2.6), проинтегрируем (2.8) по объему V с учетом теоремы Гаусса и в результате получим:
|
|
r* r |
r r |
* |
1 |
|
|
r |
r |
r |
1 |
|
r |
r |
|
||
iω |
|
ε0εk Em Em |
− |
µ0µr Hm Hm |
dV = |
∫ |
E |
H |
* dS + |
∫ |
E |
j |
* dV . |
||||
|
|
|
|
||||||||||||||
|
∫ |
2 |
|
2 |
|
|
|
|
m m |
|
m m |
||||||
V |
|
|
|
2 S |
|
|
|
|
2 V |
|
|
|
|||||
(2.9)
Для полей, изменяющихся во времени по гармоническому закону, вводится комплексный вектор Пойнтинга:
r |
1 |
|
r |
r |
|
|
Π = |
E |
H |
* . |
|||
|
||||||
|
2 |
|
m |
|
m |
|
|
|
|
|
|
||
Среднее значение комплексного вектора Пойнтинга
35

r |
1 |
r |
r |
|
r |
|
Π = |
Re E H |
* |
= ReΠ . |
|||
|
||||||
|
2 |
m |
|
m |
|
|
|
|
|
|
|
||
Соотношение (2.9) представляет |
собой |
теорему Пойнтинга в ком- |
||||
плексной форме.
Чтобы понять физический смысл теоремы Пойнтинга в комплексной форме, разделим вещественные и мнимые части выражения (2.9). Учтем,
что ε* = ε '+ iε '' , µ* = µ '− iµ '' . Тогда из (2.9) получим
|
r r |
|
|
|
ε |
|
r |
* r |
|
|
r r |
* |
1 |
|
|
r r |
* |
|||||||||||||
|
& |
|
|
|
|
ε '' E |
|
E |
µ µ '' H |
m |
H |
m |
|
|
|
|
|
|||||||||||||
Re ∫ |
ΠdS |
= − ω ∫ |
|
|
0 |
|
|
m m |
+ |
|
0 |
|
|
|
|
dV − |
|
|
|
Re ∫ |
Em jmdV ; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
S |
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.10) |
||
|
|
r r |
|
|
ε |
|
r* r |
|
µ |
r r |
* |
1 |
|
r r |
* |
|||||||||||||||
|
|
& |
|
|
|
|
|
ε ' E |
E |
|
µ ' H |
m |
H |
m |
|
|
|
|
||||||||||||
Im ∫ |
ΠdS |
= ω ∫ |
|
0 |
|
m m |
− |
0 |
|
|
|
dV − |
|
|
|
Im ∫ Em jmdV . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
S |
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.11) |
||
Выражение (2.10) есть уравнение среднего баланса энергии при гармонических колебаниях. Левая часть уравнения дает средний поток активной мощности через поверхность S, ограничивающую рассматриваемый объем V. Первый член в правой части равен средней мощности потерь в объеме V, обусловленной потерями проводимости, потерями переполяризации диэлектрика (ε '' ≠ 0) или потерями перемагничивания (µ '' ≠ 0) . В частности, если потери обусловлены только проводимостью среды, то
σ
ε '' =
ωε0
ный вид
, µ '' ≠ 0 и первый член в правой части (2.10) приобретает привыч-
|
|
|
1 |
r r |
|
P |
пот = |
∫ σEm Em* dV . |
|
|
|
|||
2 |
V |
|||
|
|
|
|
|
Второе слагаемое правой части уравнения (2.10) характеризует среднюю мощность источников, если они имеются в объеме. В частности, если потери в среде, заполняющей объем, отсутствуют, т. е. ε '' = 0 и µ '' = 0 , то вся мощность источников идет на излучение через поверхность объема:
|
r r |
1 |
r r |
|
Re ∫ |
ΠdS = − |
Re ∫ Em jm* dV . |
||
2 |
||||
S |
|
V |
||
|
|
36

Если объем заполнен средой с потерями, а источники внутри объема отсутствуют, то активная мощность, рассеиваемая в объеме, поступает в объем через его поверхность:
|
r r |
|
r* r |
Re ∫ |
ΠdS = − ω ∫ |
|
ε0ε '' Em Em |
|
|||
|
|
|
2 |
S |
V |
||
|
r |
|
r |
* |
|
|
µ µ '' H |
m |
H |
||
+ |
0 |
|
m |
dV . |
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
Из приведенного рассмотрения выражения (2.10) следует, что средним значением комплексного вектора Пойнтинга характеризуется плотность потока активной мощности. По аналогии с теорией электрических цепей величины, входящие в выражение (2.11), называют реактивным по-
током мощности и реактивными мощностями.
Излучатель
r
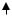 ez
ez
R
r
ex
r ey
r er
В пределах этой области волну можно считать плоской
Рис. 2.3. Сферическая волна, излучаемая диполем. Выделен квадрат, в пределах которого волну можно считать плоской
Вектор Пойнтинга волны в свободном пространстве. На рис. 2.3
показана схема образования сферической волны, излученной диполем, расположенным в начале сферической системы координат. Ограничимся рассмотрением выделенной области, в пределах которой волну можно считать плоской.
37
Рассмотрим плоскую электромагнитную волну, вектор E которой в декартовой системе координат имеет только одну составляющую (см. рис.
2.4):
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
||
|
|
|
r |
|
r |
|
i(ωt −kz ) |
|
|||||||||
|
|
|
E = ex Eme |
|
|
|
|
|
|
. |
|||||||
Чтобы найти напряженность магнитного поля H , используем уравне- |
|||||||||||||||||
ние Максвелла: rot E = −iωµ0H . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставив в это уравнение |
|
|
r |
|
r |
|
|
∂E |
x |
|
|
получим |
|||||
|
rot E = e |
y |
|
|
, |
||||||||||||
∂z |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
r |
r 1 |
|
∂E |
|
|
r |
|
|
−ik |
|
r |
||||||
|
x |
|
|
|
|
E ei(ωt −kz). |
|||||||||||
H = e |
|
|
|
|
= e |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y −iωµ0 ∂z |
|
y |
|
−iωµ0 |
m |
||||||||||
Воспользовавшись выражением для
r
E
r r
Π, k
r
H
Рис. 2.4. Взаимная ориентация векторов напряженностей электрического и магнитного полей, вектора Пойнтинга и волнового вектора для плоской волны в свободном пространстве
волнового вектора k = ω
 ε0µ0 , получим
ε0µ0 , получим
Ex |
= |
ωµ0 |
= |
ωµ0 |
|
= |
µ0 |
. |
|
|
|
|
|
|
|
||||
H y k |
ω ε0µ0 |
|
|
ε0 |
|||||
Отношение напряженностей электрического и магнитного полей плоской волны имеет единицу измерения сопротивления, обозначается буквой Z0 и называется
волновым сопротивлением свободного про- странства:
Z0 = 
 µ0
µ0 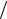 ε0 .
ε0 .
( Z0 – очень важная величина в электродинамике);
|
|
|
|
4π 10−7 |
|
|
µ0 |
= |
|
= 120π Ом = 377 Ом. |
|||
|
|
1 |
|
|||
ε0 |
10−9 |
|
||||
|
|
|||||
|
|
|
|
36π |
|
|
Итак, для плоской волны в свободном пространстве
r |
r |
|
|
r |
r |
|
E |
||
E = e |
E |
e−ikzeiωt |
; H = e |
|
m |
e−ikzeiωt . |
|||
|
|
||||||||
|
|
x |
m |
|
|
|
y |
Z0 |
|
Таким значениям векторов E и H соответствует вектор Пойнтинга
38
r |
1 |
r |
* |
r |
|
Em |
|
2 |
|
|||
|
|
|
||||||||||
|
|
|
|
|||||||||
Π = |
|
|
E, H |
|
= e |
|
|
|
|
|
|
. |
2 |
z |
|
2Z |
|||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|||
По направлению вектор Пойнтинга совпадает с направлением волнового вектора k . На рис. 2.4 показана взаимная ориентация векторов
r r r
E, H ,Π, k .
В качестве примера оценим, какова максимально возможная плотность мощности электромагнитной волны в сухом воздухе при атмосферном давлении (пробивная напряженность воздуха при этих условиях
E = 3 106 |
В/м): |
|
|
|
|
пр |
|
|
|
|
|
|
Π = |
Em2 |
= |
9 1012 |
= 1, 2 1010 Bт/м2 = 1,2 МBт/см2. |
|
2Z0 |
2 377 |
|||
|
|
|
|
||
Еще одна оценка величин. Поток мощности света от Солнца, находящегося в зените, составляет 1,5 кВт/м2. Это значение соответствует амплитуде напряженности электрического поля световой волны
|
|
|
|
= |
|
103 В/м . |
E |
= 2Z |
Π |
2 377 1500 |
|||
m |
0 |
|
|
|
|
|
Распространение группы волн (волнового пакета) сопровождается переносом энергии. Группа волн распространяется с групповой скоростью vгр. Отсюда можно заключить, что и перенос энергии электромагнитной
волной происходит с групповой скоростью. В свободном пространстве (вакууме) групповая скорость равна скорости света.
Перенос энергии электромагнитной волной означает и перенос механического импульса. При любом отражении волна передает отражателю импульс. Передача импульса образует давление волны на предмет, от которого она отражается. Русский физик Петр Николаевич Лебедев (1855 – 1912) в 1899 г. экспериментально обнаружил и измерил давление света. Эксперименты П. Н. Лебедева стали важнейшим подтверждением правильности теории Дж. К. Максвелла.
39
2.3. Теорема взаимности в электродинамике
Перенос энергии или передача сигнала происходят от источника энергии к потребителю энергии или от источника сигнала к приемнику. Возникает вопрос, изменяются ли свойства
|
I1 |
I2 |
среды либо электрических цепей, по |
|||||||
|
|
|
|
|
|
|
||||
1 |
|
|
2 |
|
|
которым происходит передача энер- |
||||
|
|
|
|
|
|
|
||||
U |
U |
гии или сигнала, от направления этой |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
передачи. |
В |
природе существуют |
|
|
–I1 |
–I2 |
||||||||
|
электрические цепи и такие среды, в |
|||||||||
|
|
|
|
|
|
|
||||
Рис. 2.5. Напряжение и ток на входе и |
которых |
распространяются электро- |
||||||||
на выходе четырехполюсника |
|
|
|
магнитные волны, что их свойства не |
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
зависят от направления распростране- |
|||
|
|
|
|
|
|
ния волны или направления протека- |
||||
e 0 |
|
|
IL O A D |
|||||||
|
|
|
|
|
|
|
ния тока. Такие цепи и среды называ- |
|||
~ |
|
|
А |
|||||||
|
|
ются взаимными. Существуют цепи и |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
среды, свойства которых зависят от |
|||
|
|
|
|
|
|
|
||||
Рис. 2.6. Генератор ЭДС и нагрузка в |
направления |
распространения волны |
||||||||
виде амперметра с нулевым внутрен- |
или от направления протекания тока. |
|||||||||
ним сопротивлением (к определению |
||||||||||
Такие цепи и среды называются не- |
||||||||||
свойств взаимного четырехполюсника) |
||||||||||
IL O A D
А
e0
~
взаимными.
Рассмотрим линейный четырехполюсник (рис. 2.5). Электрическая цепь описывается Y- или Z-матрицей:
Рис. 2.7. Генератор ЭДС и амперметр переставлены. Если показания амперметра не меняются, четырехполюсник взаимен
I1 = U1y11 + U2 y12; I2 = U1y21 + U2 y22;
|
I |
|
|
|
U |
|
|
1 |
|
= |
Y |
1 |
. |
I2 |
|
|
|
U2 |
|
|
Определение: электрическая цепь называется взаимной, если ее
Y- или Z-матрица симметрична, т. е.
Y12 = Y21, Z12 = Z21. |
(2.12) |
40 |
|

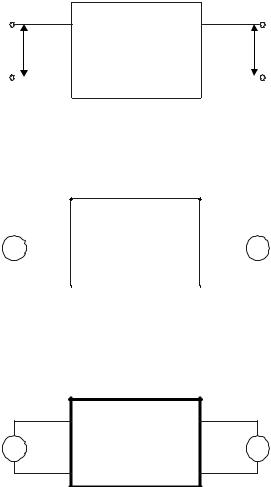
Следствие: если во взаимной цепи поменять местами источник ЭДС и амперметр, то показания амперметра не изменятся.
Это утверждение иллюстрируется рис. 2.6 и 2.7. Полагаем, что ЭДС источника e0 , а внутреннее сопротивление амперметра равно нулю. Тогда U1 = e0 , следовательно,
U2 = 0; I2 = e0 y21.
Поменяем местами источник ЭДС и амперметр. Тогда U1 = 0 ;
I1 = e0 y12 .
Если условие (2.12) выполнено, то I2 Аналогично обстоит дело и в слу-
чае СВЧ-канала передачи сигналов (рис. 2.8): если цепи питания антенн и среда между антеннами обладают свойствами взаимности и если поменять местами генератор и приемник излучения, то показания индикатора на
шкале приемника не изменятся. В электродинамике доказывается
теорема взаимности. Эта теорема оп-
ределяет условия, при которых электрическая цепь или среда, в которой распространяется волна, обладают свойствами взаимности.
При обсуждении экспериментальных иллюстраций проявления взаим-
ности электрических цепей нужно помнить о сформулированном ранее условии, что цепи линейны. В противном случае можно представить себе эксперимент, когда генератор мощностью несколько киловатт меняется местами с высокочувствительным приемником (рис. 2.8), связанным с небольшой антенной. При такой замене небольшая антенна приемника под действием мощности генератора просто сгорит, это будет проявление не- линейности электродинамических свойств небольшой антенны приемника.
41

Теорема:
•если электродинамическая система (цепь) заполнена средой со скаляр- ной диэлектрической и магнитной проницаемостями, то такая систе-
ма (цепь) взаимна.
Прежде чем доказать сформулированную теорему, рассмотрим следующее соотношение, известное в электродинамике как лемма Лоренца*, которая формулируется так:
•если имеются два источника когерентных колебаний, то в линейной среде, имеющей скалярную диэлектрическую и магнитную проницаемо-
сти, справедливо следующее соотношение: |
|
|
|
r r |
r r |
, |
(2.13) |
div{ Ea Hb |
− Eb Ha } = 0 |
||
где Ea , Ha – электромагнитное поле, созданное источником a ; Eb , |
Hb |
||
– поле, созданное источником b . Источники могут быть расположены произвольно.
Соотношение (2.13) верно, если диэлектрическая и магнитная проницаемости среды, в которой существует поля, возбужденные источниками а и b, скалярны, т. е. ε и – скаляры. Лемма Лоренца является следствием уравнений Максвелла.
Применим к формуле (2.13) соотношение из векторной алгебры, которым уже неоднократно пользовались:
r r |
r r |
r |
r r |
r |
r |
r r |
r |
div{ Ea Hb |
− EbH a } = Hb rot Ea − Ea rot Hb − Ha rot Eb + Eb rot Ha. |
||||||
Используя уравнения Максвелла, исключим роторы из полученного соотношения.
Тогда получим
|
r r |
r r |
|
|
|
|
|
div{ Ea Hb − |
EbHa } = |
|
|
|
|
||
r |
r |
r |
r |
r |
r |
r |
r |
= Hb (−iωµHa ) − Ea (iωεEb ) |
− Ha (−iωµHb ) + Eb (iωεEa ). (2.14) |
||||||
Если магнитная и диэлектрическая проницаемости являются скаляра- |
|||||||
ми, можно |
записать |
следующие |
равенства: |
HbµHa = HaµHb и |
|||
EbεEa = EaεEb .
Подставив данные равенства в правую часть равенства (2.14), убедимся, что эта часть равенства равна нулю. Таким образом, справедливость
*Хендрик Антон Лоренц (1853 – 1928) – нидерландский физик-теоретик.
42
