
electrodynamics
.pdfr |
∂A |
|
|
|
E = −µµ0 |
− grad ϕ. |
(3.9) |
||
|
||||
|
∂t |
|
||
Согласно выражению (3.9), напряженность электрического поля может быть разделена на вихревую и потенциальную части, причем вихревая часть имеет место только в случае изменяющихся во времени полей.
Таким образом, напряженности поля E и H выражаются через электродинамические потенциалы A и ϕ с помощью соотношений (3.6) и (3.9), и для описания электромагнитных полей достаточно знать четыре потен-
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||
циальные функции – три проекции |
A(Ax , Ay , Az ) и ϕ . |
|
|
|
|||||||||||||||||||||
Получим дифференциальные уравнения для электродинамических по- |
|||||||||||||||||||||||||
тенциалов A и ϕ . Для этого в уравнения Максвелла |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
r |
|
∂D |
|
|
r |
|
|
|
|
|
|
||||||||
|
|
|
|
|
rot H = |
|
|
+ j ; div D = ρ |
|
|
|
|
|
||||||||||||
|
|
|
|
∂t |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
подставим выражения (3.6) и (3.9): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
r |
r |
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 r |
||||
rot rot A = j − εε |
|
|
|
|
(grad ϕ) − εε µµ |
|
|
A |
; |
||||||||||||||||
|
|
|
|
0 ∂t |
|
||||||||||||||||||||
|
|
|
|
|
|
|
0 ∂t |
0 |
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
r |
|
|
|
|
(3.10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
− div grad ϕ − µµ0 |
|
div A = |
ρ |
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
εε0 |
|
|
|
|
|
|
|||||
Воспользуемся известным соотношением векторной алгебры: |
|||||||||||||||||||||||||
|
rot rot A = grad div A − A . |
|
|
|
|
|
|
||||||||||||||||||
Тогда (3.10) можно переписать так: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
∂ϕ |
∂2 A |
|
r |
||||||||
− A + grad div A + εε0 |
|
|
+ ε0µ0εµ |
|
|
|
= j; |
||||||||||||||||||
|
|
∂t 2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
(3.11) |
|||||||||
|
|
|
|
∂ |
|
r |
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Δϕ + µµ |
|
|
(div A) = − |
|
. |
|
|
|
|
|
|
||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
∂t |
|
|
|
|
|
|
|
|
εε0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Дифференциальные уравнения (3.11) связывают электродинамические |
|||||||||||||||||||||||||
потенциалы ( A и ϕ ) |
с источниками – с зарядами и с токами ( ρ и j ). |
||||||||||||||||||||||||
Наложим дополнительное условие, позволяющее разделить уравнения |
|||||||||||||||||||||||||
для потенциалов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
∂ϕ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
div A + εε0 |
|
= 0 . |
|
|
|
|
(3.12) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|||
53

Условие (3.12) называется условием калибровки Лоренца. Используя калибровку Лоренца, можем систему уравнений (3.11) переписать в более простом виде:
r |
|
∂ |
2 r |
|
r |
||
A − εε µµ |
|
A |
= − j; |
||||
|
∂t 2 |
||||||
0 |
0 |
|
(3.13) |
||||
|
|
∂2ϕ |
|
||||
Δϕ − εε µµ |
|
= − |
ρ |
||||
|
|
|
|
|
. |
||
|
|
|
|
|
|||
0 |
0 |
∂t 2 |
|
εε0 |
|||
Эти уравнения описывают те же физические процессы, которые описываются уравнениями Максвелла. Система уравнений (3.13) образована двумя уравнениями. Такое разделение уравнений оправдано физически: в уравнение для A входит плотность тока (токи являются источниками магнитных полей), а в уравнение для ϕ входит плотность зарядов (заряды являются источниками и стоками электрического поля). Уравнения (3.13) могут быть записаны как четыре скалярных дифференциальных уравнения
для потенциалов |
с одинаковой |
формой для всех четырех функций: |
|||
ϕ , Ax , Ay , Az . При |
j = 0 и |
ϕ = 0 |
уравнения (3.13) переходят в волновые |
||
уравнения, которые для гармонических колебаний примут вид |
|||||
|
r |
2 |
|
r |
|
|
A + |
ω |
|
εµA = 0; |
|
|
c2 |
||||
|
|
|
(3.14) |
||
|
|
|
ω2 |
|
|
|
Δϕ + |
|
εµϕ = 0. |
||
|
c2 |
||||
|
|
|
|
||
В отсутствие временной зависимости (ω → 0) уравнения (3.14) переходят, соответственно, в уравнения магнитостатики и уравнения Пуассона:
r r |
ρ . |
A = − j; Δϕ = − |
εε0
При отсутствии источников ( j = 0 и ϕ = 0 ) уравнения Пуассона превращаются в уравнения Лапласа:
A = 0; Δϕ = 0.
В отсутствие временной зависимости (ω → 0) калибровка Лоренца (3.12) примет следующий вид:
div A = 0,
который носит название «калибровка Кулона».
54
При решении задач техники СВЧ, как правило, бывает достаточно решить задачу относительно одной из четырех функций координат: ϕ , Ax , Ay , Az . Выбранная функция является скаляром, что сильно упрощает
решение используемых дифференциальных уравнений. Подчеркнём здесь, что решение дифференциальных уравнений требует формулировки граничных условий. В следующих главах настоящего курса лекций будут рассмотрены различные волноведущие структуры и найдены их свойства решением дифференциальных уравнений относительно одной из названных ранее четырех функций координат ( ϕ , Ax , Ay , Az ). При решении этих задач
будут сформулированы необходимые граничные условия. Получив решение относительно избранного электродинамического потенциала, компоненты векторов электрического и магнитного полей можно найти с помощью приведенных соотношений (3.6) и (3.9).
Рассмотрим еще один векторный потенциал. При решении некоторых задач техники СВЧ заранее известно, что электрическое поле носит вихревой характер, т. е. скалярный потенциал ϕ = 0. При этом из (3.9) и (3.12) получим
E = −iωµµ0 A; |
(3.15) |
div A = 0. |
(3.16) |
Имея в виду, что div(rot M ) = 0, где M – произвольная векторная |
|
функция, можно заключить, что из (3.16) и (3.15) следует: |
|
A = rot F , E = −iωµµ0 rot F . |
(3.17) |
Здесь вектор F представляет собой «электрический» векторный потенциал в отличие от традиционного «магнитного» векторного потенциала A . Подставив (3.17) в уравнения Максвелла, найдем, что вектор F , как и вектор A , удовлетворяет волновому уравнению. Найдя решение волнового уравнения для одного из компонентов Fx , Fy , Fz , определим компоненты
вектора напряженности электрического поля с помощью соотношения (3.17) и далее компоненты вектора напряженности магнитного поля с помощью соответствующего уравнения Максвелла. В конкретных случаях использование «электрического» векторного потенциала F облегчает решение соответствующих электродинамических задач.
55

4. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВОЛНОВОДАХ
Волновод – канал с резкими границами, по которому распространяется волна. Волноводы бывают оптические, акустические и радиоволноводы. Радиоволноводы представляют собой металлические трубы или диэлектрические стержни (диэлектрические волноводы). В своем рассмотрении ограничимся волноводами в виде металлических труб и начнем с простейшего примера – прямоугольного волновода с основным типом поля.
4.1. Основной тип поля в прямоугольном волноводе
На рис. 4.1 показан прямоугольный волновод, представляющий собой прямоугольную металлическую трубу с тщательно отполированной внутренней поверхностью.
y 
b
b
a
 z
z
Рис. 4.1. Волновод – металлическая труба, внутри которой распространяется электромагнитная волна
Для определения распределения напряженностей электрического и магнитного полей в составе электромагнитной волны в волноводе необходимо решить уравнения Максвелла с учетом граничных условий ( Eτ = 0 ) на металлических стенках волновода. Будем искать поля через векторный потенциал A , который удовлетворяет векторному волновому уравнению
r |
|
∂ |
2 ur |
|
|
A − ε µ |
|
A |
= 0. |
||
0 ∂t 2 |
|||||
0 |
|
||||
Положим, что в волноводе нет диэлектрических или магнитных вкладышей, поэтому диэлектрическая и магнитная проницаемости в волновом уравнении представлены проницаемостями свободного пространства (вакуума).
Решение уравнений Максвелла для прямоугольного волновода при
Ey ≠ 0 , Ez = Ex = 0 . Будем искать простейшее решение. Положим вектор-
ный потенциал равным
56

r = r iωt
A e y Ay (x, z)e ,
а скалярный потенциал независящим от координат и времени. Заданному таким образом векторному потенциалу соответствует div A = 0 .
Связь потенциалов и напряженностей полей:
r |
|
|
r |
|
|
|
( x, z ) |
|
E = −iωµ |
0 |
A − grad ϕ = er |
−iωµ |
0 |
A |
, |
||
r |
r |
y |
|
y |
|
|
||
|
|
|
|
|
|
|
||
H = rot A.
Отсюда получим:
Ez = Ex = 0;
Ey = −iωµ0 Ay ( x, z );
|
|
|
|
|
|
|
∂A |
|
∂Ay |
|
|
|
∂Ay |
|
|
|||||||
|
|
H |
x |
|
= |
|
|
|
|
z |
|
|
− |
|
|
= − |
|
|
; |
(4.1) |
||
|
|
∂y |
|
∂z |
∂z |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
H |
y |
|
= |
∂Ax |
|
− |
∂Az |
= 0; |
|
|
|
|||||||||
∂z |
∂x |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
∂Ay |
|
|
∂A |
|
∂Ay |
|
|
|
|||||||
|
|
H |
z |
|
= |
|
|
|
|
|
|
|
− |
|
x |
= |
|
|
|
. |
|
|
|
|
|
∂x |
|
∂y |
|
∂x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Будем искать решение в виде волны, распространяющейся вдоль оси |
||||||||||||||||||||||
волновода Z: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
= A |
f |
( x)e−iβz . |
|
|
|
|
(4.2) |
||||||||||
|
|
y |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда векторное волновое уравнение превращается в скалярное вол- |
||||||||||||||||||||||
новое уравнение относительно Ay : |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∂2 A |
∂2 A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y |
+ |
|
|
|
|
|
y |
|
+ ω2ε0µ 0 Ay = 0. |
(4.3) |
|||||||||||
|
|
|
∂ z2 |
|||||||||||||||||||
|
∂ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
с граничными условиями: Ау = 0 при x = 0 , |
x = a (так как E y = 0 при x = 0 , |
|||||||||||||||||||||
x = a ) или для введенной функции |
f (x) : |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
f (x) = 0 |
|
|
|
|
|
|
|
|
(4.4) |
||||||||
при x = 0 , x = a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂2 Ay = −βA0 f (x)e−iβz ,
∂ z2
то уравнение (4.3) можно переписать в виде
57

|
|
|
A |
f ''(x) − β2 f (x) + ω2ε µ |
f (x) e−iβz |
= 0. |
|
|
|
||
|
|
|
0 |
|
|
0 0 |
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f ''(x) + kx2 f (x) = 0, |
|
|
|
|
(4.5) |
где k |
2 |
= ω2ε µ |
− β2 |
( k |
x |
– поперечное волновое число): |
ω2ε µ |
0 |
= k 2 |
(k – |
|
|
x |
0 0 |
|
|
|
|
0 |
|
|
||
волновое число волны в свободном пространстве); β – продольное волновое число для волновода или фазовая постоянная распространяющейся волны:
β2 = k 2 − kx2. |
(4.6) |
Полученное уравнение (4.6) носит название дисперсионного уравне-
ния.
Для волновода принято обозначение β = 2π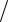 λ g , где λ g – длина волны
λ g , где λ g – длина волны
в волноводе, так что дисперсионное уравнение связывает длину волны в волноводе с длиной волны в свободном пространстве на той же частоте.
Найдем f (x) из (4.5). Решение (4.5) ищем в виде
f (x) = C1e−ikx x + C2eikx x.
Используя граничные условия (4.6), получим систему алгебраических уравнений относительно C1 и C2:
C + C = 0; |
|
|||
|
1 |
2 |
|
|
|
|
|
+ C eikxa |
= 0. |
C e−ikxa |
||||
|
1 |
|
2 |
|
Система однородных алгебраических уравнений имеет решение, если определитель системы равен нулю:
11
e−ikxa eikxa = 0,
откуда eikxa − e−ikxa = 0 или sin kxa = 0 .
Это условие может быть выполнено, если kxa = nπ , где n = 1, 2,3,... .
Разные n дают различные картины распределения поля в поперечном сечении волновода. Это – условие квантования решений уравнений Максвелла: kx = nπ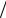 a .
a .
58

Вспомним, что k = 2π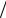 λ , где λ – длина волны в свободном пространстве. Тогда
λ , где λ – длина волны в свободном пространстве. Тогда
k |
z |
= β2 |
= (2π λ)2 |
− (nπ a )2 ; |
(4.7) |
|
|
|
|
|
|
|
|
|
|
f (x) = C sin |
nπ |
x . |
(4.8) |
|
|
|
|
||||
|
|
|
a |
|
|
|
При n = 1 функция f (х) определяет простейший тип поля прямоугольного волновода.
Распределение поля в прямоугольном волноводе в случае простей-
шего типа поля. Объединив (4.3) и (4.8), получим для случая n = 1
Ay = A0 sin π x e−iβz .
a
Используя (4.1), (4.2) и (4.7) получим:
Ez = Ex = 0 ;
Ey = −iωµ0 Ay sin π x e−iβz ;
a
|
|
|
π |
|
−iβz |
|
|
||||
H x = iβA0 sin |
|
x |
e |
|
|
; |
(4.9) |
||||
|
|
|
|||||||||
|
|
a |
|
|
|
|
|
||||
|
H y = 0; |
|
|
|
|
|
|
||||
H z = A0 |
nπ |
|
π |
|
−iβz |
|
|||||
|
cos |
|
|
x e |
|
|
; |
||||
a |
|
|
|
|
|||||||
|
|
a |
|
|
|
|
|||||
Данное решение имеет продольную компоненту магнитного поля. Та- |
|||||||||||
кое решение принято называть магнитным типом поля и обозначать символом Hn,m , где n и m – порядок квантования полученных решений вдоль
осей x и y . Полученное решение отвечает магнитному типу поля при n = 1
и m = 0.
Эпюры полей в прямоугольном волноводе при волне типа H1,0 при-
ведены на рис. 4.2.
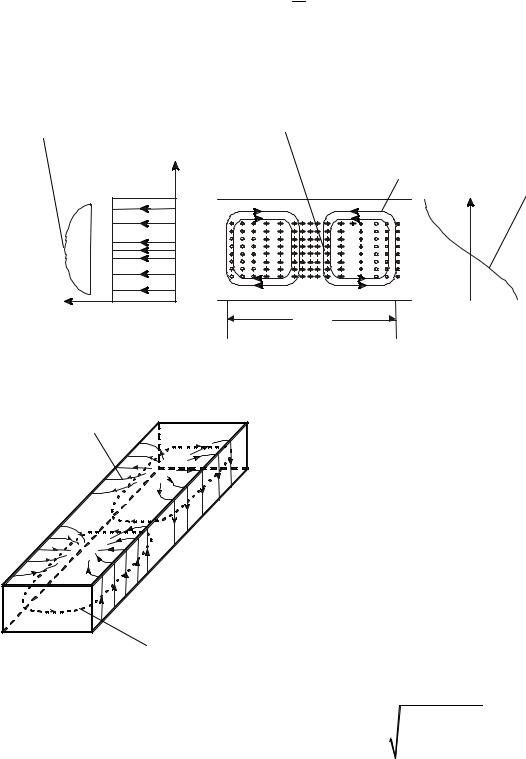
Назовем отношение Ey к H x волновым сопротивлением волновода:
Ez H x = Z g . |
|
Из (4.9) получим: |
|
Z g = ωµ0 β . |
(4.10) |
59
На рис. 4.2 показано распределение поля в фиксированный момент времени. Картина поля смещается вдоль оси z со скоростью vg :
vg = ω = vph .
β
Здесь vg – скорость движения поверхности равных фаз или фазовая скорость волны в волноводе.
E |
|
sin |
π |
x |
H x sin |
π |
x |
|
y |
|
|||||||
|
||||||||
|
|
a |
|
a |
||||
|
|
|
|
|
|
|||
a |
0 |
λ g
Hz |
Hz cos |
π |
|
|
|
x |
|
|
|
||
|
|
a |
|
Рис. 4.2. Силовые линии электрического и магнитного полей основного типа поля в прямоугольном волноводе
r |
Рис. 4.3 иллюстрирует распределе- |
|
ние силовых линий поверхностного тока |
||
jsur |
||
|
на внутренней поверхности волновода. |
|
|
Критическое значение длины вол- |
r
H
Рис. 4.3. Силовые линии тока проводимости на внутренней поверхности прямоугольного волновода с основным типом поля
ны волновода. Для рассматриваемого простейшего случая n = 1 выражение (4.7) можно переписать следующим образом:
|
2π 2 |
|
2π 2 |
|
π 2 |
|||||||||
|
|
|
|
= |
|
|
|
|
− |
|
. |
|||
λ |
|
|
|
|
|
|||||||||
|
|
|
|
λ |
|
a |
||||||||
|
|
g |
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ g = |
|
|
1 |
|
|
|
|
|
или |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
1 |
− |
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
λ2 |
(2a )2 |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
60
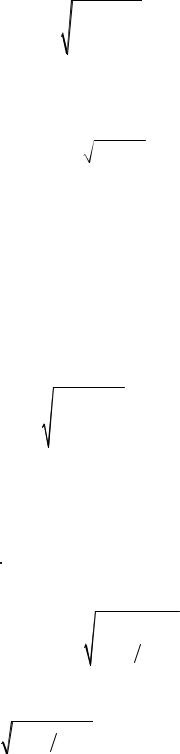
λ g = |
|
λ |
|
||||
|
|
|
|
, |
(4.11) |
||
|
|
|
|
|
|||
|
|
|
|||||
|
|
|
λ 2 |
|
|||
|
1 − |
|
|
|
|||
|
|
|
|||||
|
|
|
2a |
|
|||
где λ – длина волны в свободном пространстве.
В случае заполнения волновода средой с проницаемостью εr > 1 λ соответствует длине волны в среде, т. е.
2π λ = ω
λ = ω
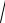 ε0εrµ0 .
ε0εrµ0 .
На рис. 4.4, а показана зависимость длины волны в волноводе λ g от
длины волны в свободном пространстве в случае вакуумного заполнения волновода.
• Электромагнитная волна, у которой длина волны в вакууме больше критической длины волны волновода ( λ > λ c ), не может распростра-
няться в волноводе. Для основного типа поля в прямоугольном волноводе
λc = 2a .
Фазовая постоянная волны в волноводе
|
2π |
|
2π |
|
λ 2 |
|
|
β = |
|
= |
|
1 − |
|
. |
(4.12) |
|
|
|
|||||
|
λ g |
|
λ |
|
λc |
|
|
При λ > λc фазовая постоянная волны в волноводе β становится мни- |
|||||||
мым числом, так что при λ > λc |
поле, возбуждающееся в волноводе, уже |
||||||
не представляет собой волну, а экспоненциально затухает без изменения фазы.
Групповая скорость волны в волноводе. Итак, фазовая скорость вол-
ны в волноводе найдена:
v = |
ω |
= |
λω |
|
|
|
1 |
|
, |
||||
|
|
|
|
|
|
||||||||
ph |
|
β |
|
2π |
1 |
− (λ λ c ) |
2 |
|
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
vph = |
|
|
|
c |
|
|
|
|
, |
|
|
(4.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
1 − ( |
λ λ |
c |
)2 |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где с – скорость света в свободном пространстве; vph → ∞ при λ → λc . |
|||||||||||||
61
Чему же равна групповая скорость волны в волноводе? Ранее получе- |
||||||||
но выражение для групповой скорости (2.2). Перепишем его еще раз: |
||||||||
|
v |
= (∂β ∂ω)−1. |
|
|
(4.14) |
|||
|
gr |
|
|
|
|
|
|
|
Представим критическую частоту ωc волновода как |
||||||||
|
ω |
|
= 2π c |
|
|
|
(4.15) |
|
|
c |
λc |
|
|
|
|
||
|
|
|
|
|
|
|
||
и запишем β как функцию ω , используя (4.12) и (4.15): |
||||||||
|
|
|
β = |
ω |
1 |
|
ω |
2 |
|
|
|
|
− |
c |
|
||
|
|
|
|
c |
|
|
ω |
|
или |
|
|
|
|
|
|
|
|
|
β2 = ω2 − ωc2 . |
|
(4.16) |
|||||
|
|
|
c2 |
|
|
|
|
|
λg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
|
|
|
|
|
ω = βc |
0 |
|
|
|
|
|
λ |
|
0 |
λ = λc = 2a |
|
|
|
β |
||||
|
|
|
|
|||||
|
|
|
а |
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
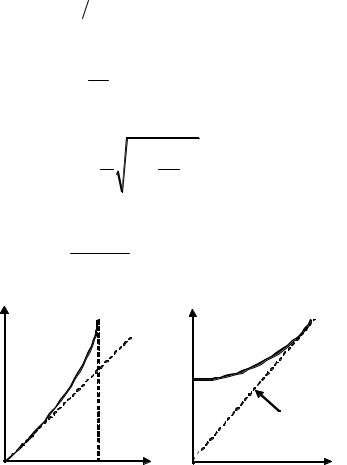
Рис. 4.4. Частотная дисперсия в радиоволноводе: а – |
||||||||
длина волны в волноводе в функции от длины волны в |
||||||||
вакууме; б – зависимость частоты от фазовой постоянной |
||||||||
Полученные соотношения иллюстрируются рис. 4.4, б. Они устанавливают ту же связь между частотой и фазовой постоянной, что и дисперсионное уравнение (4.6). Продифференцируем (4.16):
∂β |
= |
1 ∂(β2 ) |
= |
1 1 |
2ω = |
ω |
||||
|
|
|
|
|
|
|
c2β |
|||
∂ω 2β ∂ω 2β c2 |
|
|||||||||
и подставим в (4.14). Тогда зависимость групповой скорости волны в волноводе от частоты примет вид
62
