1. Содержательная (исходная) постановка задачи

Предварительные сведения

Рассматривается полином одной переменной с целочисленными коэффициентами

P_n(x) = a₀xⁿ + a₁x^n-1 + … + a_n-1x + a_n, a₀  0.

Плотное представление полинома основано на хранении последовательности (массива) всех его коэффициентов (a₀, a₁, …, a_n-1, a_n), в том числе и тех, которые равны нулю. Разреженное представление полинома использует только ненулевые коэффициенты. Например, пусть дан полином

P₇(x) = 3x⁷ + 13x² – 7 .

Его плотное представление есть (3, 0, 0, 0, 0, 13, 0, 7). Разреженное представление есть последовательность пар чисел (коэффициент, показатель степени), т. е. ((3, 7), (13, 2), (7, 0)).

В общем случае полином (многочлен) P(x) представляется последовательностью пар чисел, каждая из которых (c, d) соответствует моному (одночлену) сx^d, т. е. P(x)  (q₁, q₂, …, q_m-1, q_m), где q_k = (c_k, d_k). Удобно использовать упорядоченное разреженное представление полинома, расположив пары «коэффициентпоказатель» в порядке убывания показателей степеней мономов, т. е. так, что ( k 1..m  1: d_k > d_k+1). Во-первых, такое представление единственно, а во-вторых, многие операции над полиномами в таком представлении выполняются более эффективно.

Постановка задачи

Заданы 2 полинома одной переменной с целочисленными коэффициентами. Требуется найти их сумму и разность.

Указание. Использовать разреженное представление полиномов.

2. Анализ и пример решения задачи

Анализ задачи

1. Особенностью разреженного представления полинома является то, что нулевой полином P(x) = 0 представляется пустой последовательностью ( ), что отличается от представления числа 0.

2. Операцию вычитания полиномов P1(x)  P2(x) можно рассматривать как операцию сложения P1(x) + (P2(x)), определив предварительно одноместную операцию изменения знака полинома –P(x) или минус(P(x)). Действительно, пусть P(x)  p = (q₁, q₂, …, q_m-1, q_m), тогда определим Q(x) = минус(P(x)) так, что Q(x) 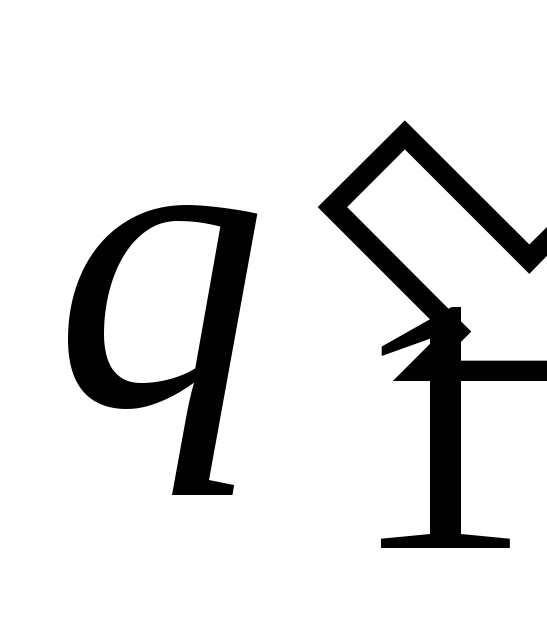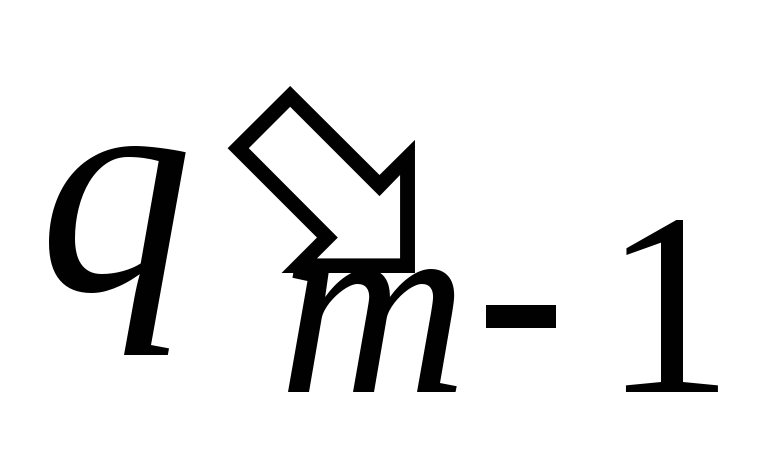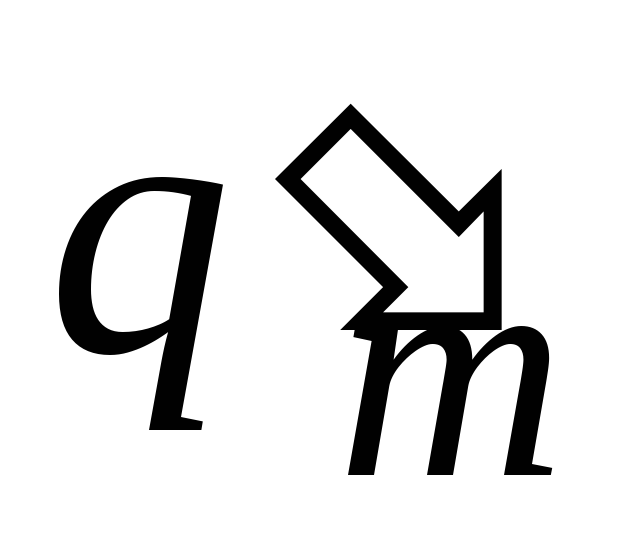 = (,, …,,), причём еслиq_k = (c_k, d_k), то 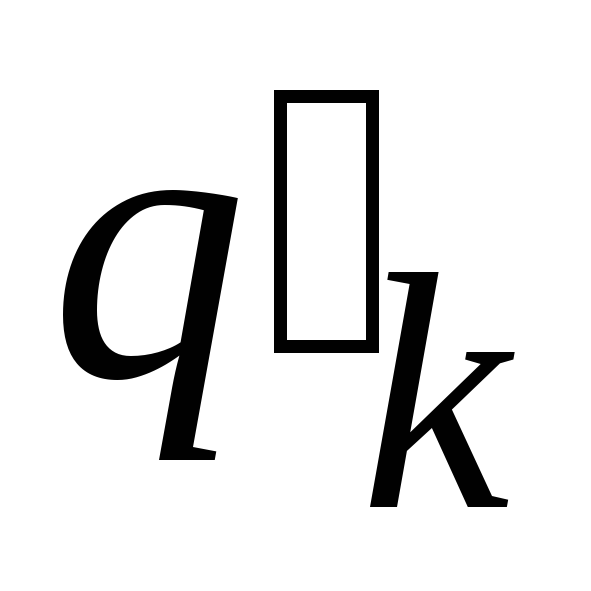= (c_k, d_k) для всех k  1..m.

3. Поскольку операции сложения и вычитания взаимно обратны, то в программе для контроля можно предусмотреть выполнение обратной операции. Например, после сложения P3(x) = P1(x) + P2 (x) можно выполнить вычитание P4(x) = P3(x)  P1(x). Очевидно, что при правильной реализации операций сложения и вычитания P4(x) = P2(x).

Пример решения задачи

Пусть P1(x) = 3x⁷+ 13x² 7 и P2(x) = 113x¹⁵+ x⁵  13x²+ x. Очевидно, что P3(x) = P1(x) + P2(x) = 113x¹⁵+ 3x⁷+ x⁵+ x  7.

Рассмотрим, как эти действия реализуются с последовательностями

p1 = ((3, 7), (13, 2), (–7, 0)),

p2 = ((113, 15), (1, 5), (–13, 2), (1, 1)).

Для удобства расположим эти последовательности друг под другом, «совместно» упорядочив их по показателям степени мономов, а результат таким же образом расположим строкой ниже:

p1 = ( (3, 7), ( 13, 2), (7, 0)),

p2 = ( (113, 15), (1, 5), (13, 2), (1, 1) );

p3 = ( (113, 15), (3, 7), (1, 5), ( 0, 2), (1, 1), (7, 0)).

Исключив пары с нулевым коэффициентом, имеем

p3 = ((113, 15), (3, 7), (1, 5), (1, 1), (–7, 0)),

что соответствует результирующему полиному. В общем случае, если m₁ и m₂ – длины входных последовательностей, а m₃ – длина выходной последовательности, то 0  m₃  m₁ + m₂. Пример для случая m₃ = 0:

p1 = ((11, 100), (–1, 0)), p2 = ((–11, 100), (1, 0)), p3 = ( ).

Пример для случая m₃ = m₁ + m₂:

p1 = ((3, 3), (1, 1)), p2 = ((4, 4), (2, 2), (1, 0)),

p3 = ((4, 4), (3, 3), (2, 2), (1, 1), (1, 0)).