
- •Теория функций комплексной переменной
- •1. Элементарные функции комплексного переменного
- •2. Условия дифференцируемости функции комплексного переменного
- •3. Интегрирование аналитических функций
- •4. Теорема единственности. Аналитическое продолжение
- •5. Особые точки. Ряды Лорана
- •6. Вычеты
- •7. Вычисление интегралов
- •Список литературы
- •Оглавление
3. Интегрирование аналитических функций
![]() В
рамках рассматриваемых здесь вопросов
важны криволинейные интегралы второго
рода от функции комплексного переменного.
Такой интеграл не требует специального
определения, так как он легко сводится
к паре криволинейных интегралов от
функций вещественного переменного:
В
рамках рассматриваемых здесь вопросов
важны криволинейные интегралы второго
рода от функции комплексного переменного.
Такой интеграл не требует специального
определения, так как он легко сводится
к паре криволинейных интегралов от
функций вещественного переменного:
![]()
![]()
для вычисления,
которых требуется провести параметризацию
кривой
![]() и
вычислить определенные интегралы:
и
вычислить определенные интегралы:

Как обычно, компактная формула векторного анализа при переходе к вычислению превращается в длинное описание. Переход от произвольной функции комплексной переменой в общем случае не меняет ситуации. Однако для замкнутых контуров картина резко меняется.
Чтобы точно описать это утверждение, нужно уточнить терминологию.
Определение.Область комплексной плоскости называется односвязной, если любой замкнутый путь в этой области можно стянуть в точку, не выходя из области.
Пример.![]() –
открытый круг,
–
открытый круг,![]() -- открытая полуплоскость, множество
-- открытая полуплоскость, множество![]() не является открытым, так как все точки
его границы не обладают требуемым
свойством, множество
не является открытым, так как все точки
его границы не обладают требуемым
свойством, множество
![]() не является открытым, так как в точке
не является открытым, так как в точке![]() не выполнено требуемое свойство. Все
перечисленные множества являются
односвязными. Область
не выполнено требуемое свойство. Все
перечисленные множества являются
односвязными. Область![]() (кольцо)
не является односвязным, множество
(кольцо)
не является односвязным, множество![]() (проколотый
круг) то же не односвязно.
(проколотый
круг) то же не односвязно.
Теорема Коши.Пусть![]() –
односвязная область
–
односвязная область![]() –
замкнутый контур внутри области. Тогда
интеграл от аналитической в области
–
замкнутый контур внутри области. Тогда
интеграл от аналитической в области![]() функции
функции![]() контуру
контуру![]() равен нулю:
равен нулю:![]()
Доказательство.Условия Коши –
Римана и формула Грина
и формула Грина гарантируют равенство нулю вещественной
и мнимой части интеграла.
гарантируют равенство нулю вещественной
и мнимой части интеграла.
Первое важное следствие теоремы Коши – формула, дающая интегрально представление аналитической функции.
Следствие (формула Коши).Если![]() аналитическая функция в односвязной
области
аналитическая функция в односвязной
области![]() ,
,![]() – положительно ориентированный замкнутый
контур, лежащий в области, и точка
– положительно ориентированный замкнутый
контур, лежащий в области, и точка![]() находится внутри контура, то справедливо
равенство:
находится внутри контура, то справедливо
равенство:
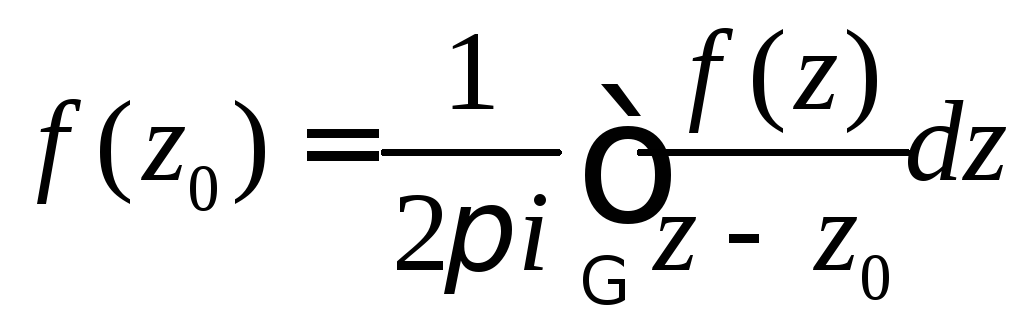
Доказательство.Простое, но очень
важное доказательство этой формулы
основано, вытекающей из теоремы Коши,
независимости интеграла от выбора
контура. В формуле Коши подынтегральная
функция является аналитической всюду,
кроме точки![]() .
.
Покажем, что интеграл по контуру
![]() равен интегралу по контуру
равен интегралу по контуру![]() --
положительно ориентированной окружности
маленького радиуса (
--
положительно ориентированной окружности
маленького радиуса (![]() ).
Рассмотрим вспомогательный контур
).
Рассмотрим вспомогательный контур![]() ,
здесь
,
здесь![]() дуга соединяющая контуры
дуга соединяющая контуры![]() и
и![]() ,
пройденная дважды в разных направлениях,
,
пройденная дважды в разных направлениях,![]() контур
контур![]() ,
пройденный в отрицательном направлении.
При такой компоновке
,
пройденный в отрицательном направлении.
При такой компоновке![]() окажется замкнутым контуром, внутри
которого функция
окажется замкнутым контуром, внутри
которого функция![]() аналитична, следовательно
аналитична, следовательно .
Стандартные свойства криволинейных
интегралов второго рода позволяют
получить формулу
.
Стандартные свойства криволинейных
интегралов второго рода позволяют
получить формулу .
Простые вычисления показывают, что
интеграл по контуру
.
Простые вычисления показывают, что
интеграл по контуру![]() стремится к
стремится к![]() при
при![]() ,
с другой стороны все такие интегралы
равны интегралу по контуру
,
с другой стороны все такие интегралы
равны интегралу по контуру![]() .
Следовательно:
.
Следовательно:

Формула Коши позволяет получить много интересной и полезной информации об аналитических функциях. Первый шаг в этом направлении – формула для производных аналитических функций.
Следствие (формула для производных).Если![]() аналитическая функция в области
аналитическая функция в области![]() ,
,![]() – положительно ориентированный замкнутый
контур, лежащий в области, и точка
– положительно ориентированный замкнутый
контур, лежащий в области, и точка![]() находится внутри контура, то функция
имеет в этой точке производные всех
порядков, причем справедливо равенство:
находится внутри контура, то функция
имеет в этой точке производные всех
порядков, причем справедливо равенство:
 .
.
Легко дать прямое доказательство этой теоремы, но важно понимать, что формула является следствием теоремы о дифференцировании интеграла по параметру.
Теорема.Если функция![]() дифференцируема по
дифференцируема по![]() и интегралы
и интегралы сходятся равномерно (т. е.
сходятся равномерно (т. е.![]() ,
,
![]() ),
то интеграл можно дифференцировать по
параметру
),
то интеграл можно дифференцировать по
параметру

Отметим, что такое поведение совершенно
не свойственно неаналитическим функциям
одной переменной, которые могут иметь
производную
![]() -го
порядка, но не иметь производной
-го
порядка, но не иметь производной![]() -го
порядка. Это различие идет и дальше.
Функция
-го
порядка. Это различие идет и дальше.
Функция![]() может быть непрерывно продолжена в
может быть непрерывно продолжена в![]() ,
,![]() ,
то же справедливо в отношении всех ее
производных
,
то же справедливо в отношении всех ее
производных![]() .
Таким образом мы получаем пример
бесконечно дифференцируемой функции,
которую нельзя представить в виде ряда
Тейлора, но для аналитических функций
такое не возможно.
.
Таким образом мы получаем пример
бесконечно дифференцируемой функции,
которую нельзя представить в виде ряда
Тейлора, но для аналитических функций
такое не возможно.
Следствие (ряд Тейлора для аналитической
функции).Если![]() аналитическая функция в области
аналитическая функция в области![]() ,
точка
,
точка![]() находится внутри контура, то в круге
находится внутри контура, то в круге![]() расстояние от точки
расстояние от точки![]() до границы области
до границы области![]() ,
функция допускает разложение в ряд
Тейлора:
,
функция допускает разложение в ряд
Тейлора:

Доказательство.Положим![]() .
Окружность лежит в области
.
Окружность лежит в области![]() ,
и точка
,
и точка![]() лежит внутри окружности. Воспользуемся
формулой Коши
лежит внутри окружности. Воспользуемся
формулой Коши

Преобразуем выражение так, что бы дробь
![]() можно было бы разложить по формуле
геометрической прогрессии
можно было бы разложить по формуле
геометрической прогрессии
 ,
,
здесь мы
воспользовались тем, что
![]() .
Подставим это разложения в интеграл и
поменяем местами интеграл и сумму:
.
Подставим это разложения в интеграл и
поменяем местами интеграл и сумму:
 .
.
Доказанная формула позволяет дать еще одно эквивалентное определение аналитичности: функция является аналитической в области, если она допускает разложение в ряд Тейлора в окрестности любой точки.
Локальные свойства аналитических функций, описные выше, оказывают существенное влияние на поведение функции в целом.
