2. Условия дифференцируемости функции комплексного переменного

Выясним условия, гарантирующие наличие производной у функции комплексного переменного, т. е. наличие предела

Рассмотрим эквивалентное «вещественное» описание этого вопроса

_.

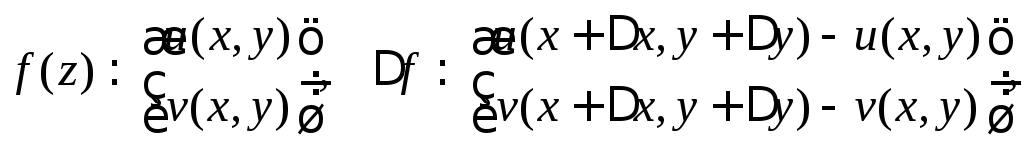
Если устремить приращения аргументов к нулю, то получится следующее соотношение для дифференциалов

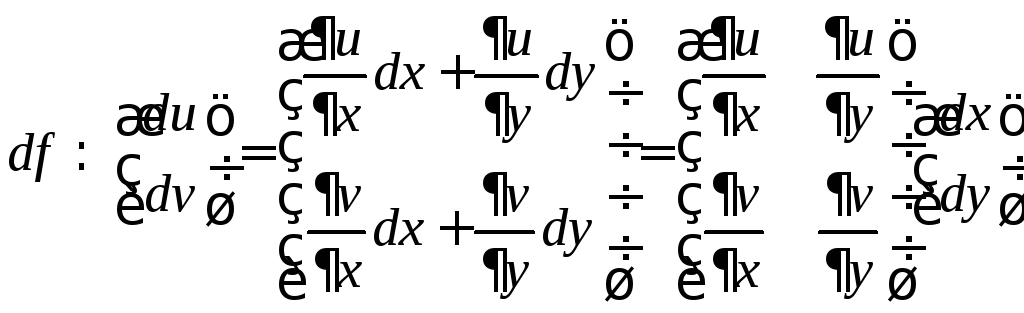
Требуется выяснить, при каких условиях найдется комплексное число такое, что, т. е.

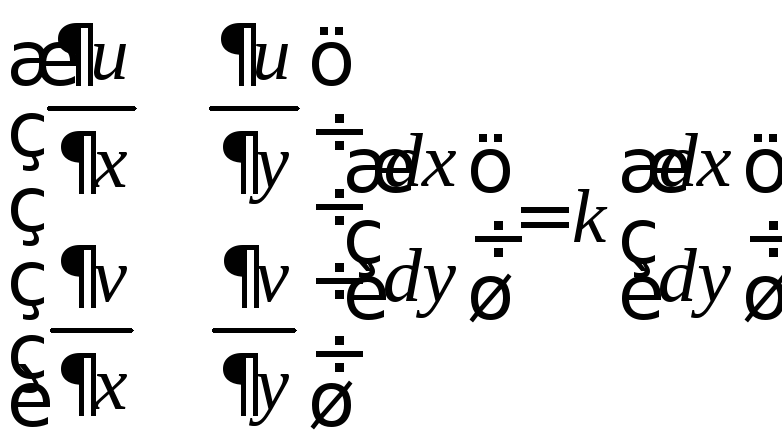
Заметим, что умножение вектора на комплексное число означает растяжение с коэффициентоми поворот на угол. Воспользуемся матричным описание этих действий и получим равенство

Из этого равенства следует требуемое условие, которое можно сформулировать в виде теоремы.

Теорема (условие Коши-Римана).Функция комплексного переменного дифференцируема тогда и только тогда, когда выполнены равенства

– условия Коши-Римана.

Определение.Функцияназывается аналитической в области, если в каждой точке области выполнено условие Коши-Римана.

Напомним, что областью называется любое подмножество комплексной плоскости такое, что каждая точка входит в него вместе с окрестностью (достаточно малым кругом с центром в этой точке).

Легко привести примеры функций удовлетворяющих условию Коши-Римана в одной единственной точке, но важными являются именно аналитические функции. Только о них и будет идти речь в дальнейшем.

Из анализа доказательства условий Коши-Римана вытекает полезная геометрическая интерпретация: в малой окрестности точки аналитическая функция действует как линейная, при этом – сдвиг,– локальный коэффициент растяжения, а– локальный угол поворота, осуществляемый отображениемв точке.

Следствие.Пусть функцияаналитическая в областитогда

1) если кривая в области, и, то длина кривойравна(криваяполучается из кривой«растяжением», коэффициент растяжение в точкеравен).

2) если область содержится в области, и, то площадь областиравна, (локальный коэффициент растяжения одинаков во всех направлениях, поэтому квадрат со сторонойперейдет в квадрат со стороной).

3) если две кривые лежат в области, пересекаются в точкепод углом(т. е. касательные к кривым в этой точке образуют угол), то образы этих кривых при отображениипересекаются в точкепод тем же углом.

Задача.Покажите, что элемент дуги кривойравен. Указание. Рассмотрите параметрическое описание кривой.

Примеры.1) Вычислим длину образа отрезкапри отображении.

Решение. , для вычисления интеграла надо ввести параметризацию кривой

Теперь можно вычислить длину образа

.

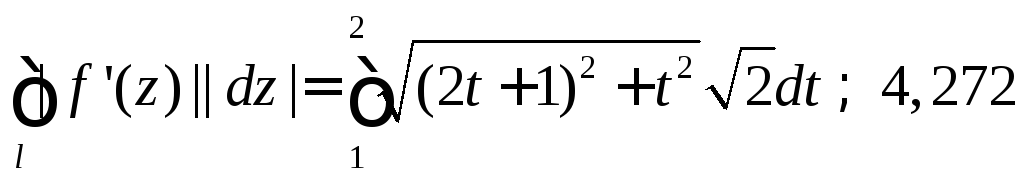2) Вычислим площадь образа квадрата при отображении.

Решение.,

площадь равна .

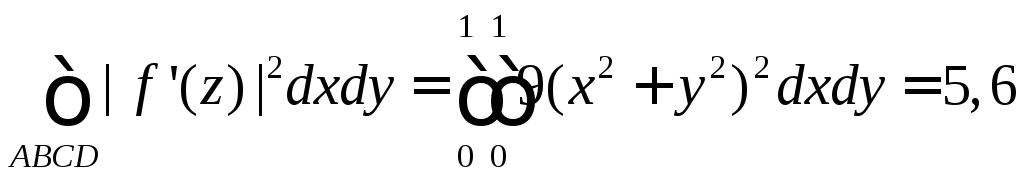3) Образ квадрата при дробно-линейном отображении

_{Чтобы контролировать отображения надо выяснить, во что перейдут прямые, составляющие границы квадрата. Эта задача сводится к рассмотренной ранее инверсии, если предварительно разложить дробно-линейную функцию на компоненты}

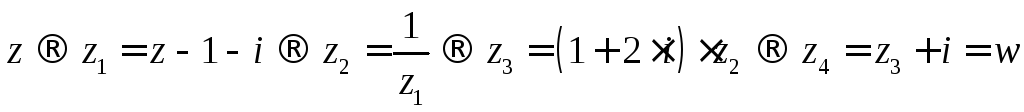
О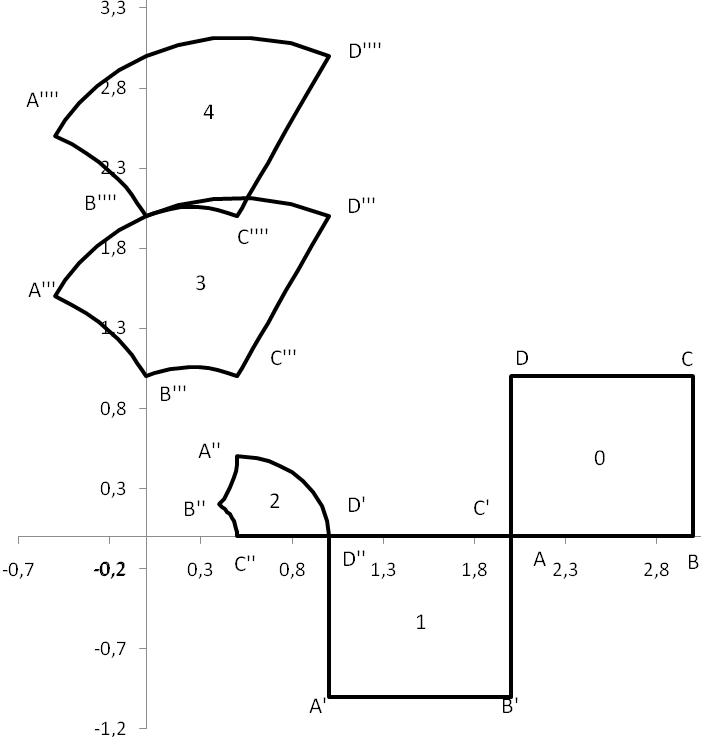бозначим. Действительная часть -xи мнимая часть -yс соответствующими индексами являются координатами образов точкиz, получаемых в результате последовательных преобразований.

П

Рис.1

остроим изображения квадрата, выписывая формулы преобразования координат для каждого шага (Рис.1). Вершины квадрата и их последовательные образы будем обозначать одними и теми же буквами с соответствующим количеством штрихов на каждом изображении. Так,это вершины исходного квадрата,- вершины квадрата после первого шага отображения и т.д. Цифра внутри квадрата обозначает номер преобразования, 0 – исходный квадрат. Вообще говоря, квадрат будет получаться криволинейным, но углы при вершинах будут оставаться прямыми. Будет также сохраняться ориентация квадрата: внутренность квадрата на каждом изображении будет находиться слева от точки, движущейся по границе в направлении отк.

Шаг 1. Формулы преобразования координат:

.

Это преобразование задает параллельный перенос исходного квадрата вниз и влево на единицу.

Шаг 2. Формулы преобразования координат:

.

Данное преобразование задает инверсию. Заметим, что отрезки , и переходят в дуги окружностей, а отрезок сохраняется прямолинейным, точка остается неподвижной.

Шаг 3. Формулы преобразования:

Это преобразование задает поворот вокруг начала координат на угол против часовой стрелки и растяжение враз.

Шаг 4. Формулы преобразования координат:

Это преобразование задает сдвиг на единицу вверх по оси y.

4) Вычислим периметры последовательных изображений квадрата из предыдущего примера, обозначения сохраняются.

Периметр изображения 1 равен периметру изображения 0: .

Вычислим периметр изображения 2 – криволинейного квадрата :

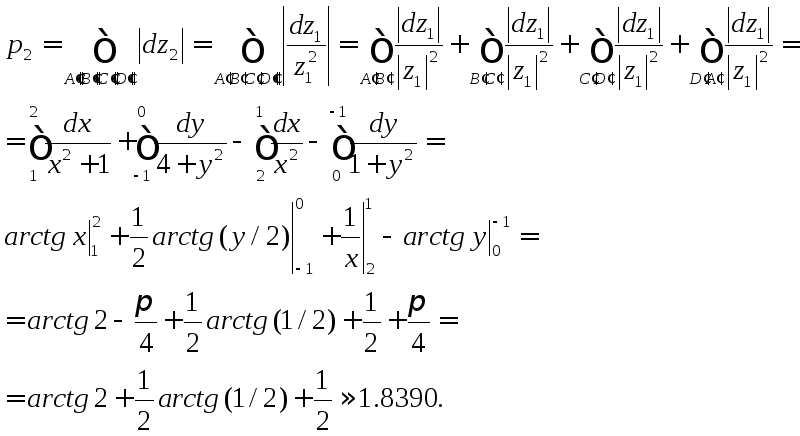
Изображение 3 получается из изображения 2 поворотом и растяжением в раз, а изображение 4 – сдвигом изображения 3. Поэтому

.