©

И. Н. СМИРНОВ

МОДЕЛИРОВАНИЕ СТАЦИОНАРНЫХ ТЕПЛОВЫХ ПОЛЕЙ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ

ПО ДИСЦИПЛИНЕ «МОДЕЛИРОВАНИЕ СИСТЕМ»

Санкт-Петербург

2012

СОДЕРЖАНИЕ

1. Цель работы………………………………………………….…………3

2. Решение плоской задачи стационарной теплопроводности

методом сеток…………………………………..……………….……...3

3. Подготовка данных для моделирования……………………….……..6

4. Настройка и выполнение программы…………….…………….……..8

5. Задание 1: исследование влияния числа делений сетки на

результаты моделирования….…………………….…………...............10

6. Задание 2: исследование влияния допустимой погрешности

приближений на результаты моделирования………....…………..….12

7. Задание 3: исследование влияния параметра границы на

результаты моделирования…………..…………..……..…………….12

8. Задание 4: снятие статических характеристик теплового объекта

управления…………………….…………...…………………………..13

9. Задание 5: исследование температурного поля аппарата

для термообработки химического волокна……...................…...….16

10. Содержание отчета………...………………………………………….18

1. Цель работы

Целью лабораторной работы является исследование компьютерных моделей стационарных температурных полей в областях плоскости, ограниченных замкнутыми контурами. Модели базируются на методе сеток − численном методе решения уравнений в частных производных. Для их реализации используется программа, разработанная в среде Turbo-C. В задачи исследования входит анализ точности моделей, а также влияния некоторых настроек моделей на результаты моделирования.

Упомянутые области можно рассматривать, в частности, как сечения плоскостью трехмерных тел, являющихся объектами регулирования температуры. В случае существенной зависимости температуры от пространственных координат такие тела относят к категории объектов с распределенными параметрами. При их изучении представляют интерес статические характеристики как зависимости установившихся значений температуры в отдельных точках объекта от воздействий со стороны нагревателей или внешней среды. Получение на моделях статических характеристик также входит в задачи работы.

2. РЕШЕНИЕ ПЛОСКОЙ ЗАДАЧИ СТАЦИОНАРНОЙ

ТЕПЛОПРОВОДНОСТИ МЕТОДОМ СЕТОК

Использованная в заголовке краткая формулировка означает, что требуется найти зависимость установившейся температуры T(x,y) как функции декартовых координат x, y в связной (не распадающейся на две или более части) области G, ограниченной замкнутым контуром (границей) Г (рис. 1). Характер зависимости определяется условиями теплообмена на границе (граничными условиями).

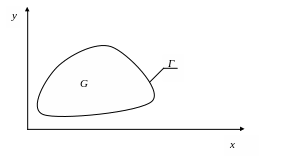
Рис. 1

В отсутствие внутренних источников тепла (далее это предполагается) температура удовлетворяет уравнению Лапласа

(1)

В отсутствие явлений излучения (это также предполагается) граничные условия имеют следующий общий вид:

. (2)

Квадратные скобки с символом «Γ» указывают, что в левой части этого равенства фигурирует температура Т и ее производная по внешней нормали n к поверхности, взятые на границе. Параметры , ,  определяются физической сутью процессов теплообмена, происходящих на отдельных участках границы. Возможны следующие частные случаи.

1. Интенсивный теплообмен, при котором температура границы практически совпадает с температурой окружающей среды Т_с . Тогда

 = 0,  =1,  =Т_с. (3)

2. Полное отсутствие теплообмена (идеальная теплоизоляция). Тогда

 =1,  = 0,  = 0. (4)

Так же выглядят условия, когда граница проходит по оси симметрии области (разделяет зеркально повторяющие друг друга части области).

3. Промежуточный случай ограниченного по интенсивности теплообмена со средой. Тогда

 = λ,  = γ,  = γT_c , (5)

где λ – коэффициент теплопроводности материала области, а γ  коэффициент теплоотдачи на границе.

Примечание. Для упрощения ввода данных программой моделирования предусмотрено автоматическое умножение T_c на γ, поэтому при работе с ней достаточно ввести

 = λ,  = γ,  = T_c . (6)

4. На границе расположен источник тепла, создающий удельный тепловой поток H (количество тепла, передаваемое источником внутрь области в единицу времени через поверхность с единичной площадью). Тогда

 = λ,  = 0,  = H. (7)

Согласно методу сеток решение ищется не во всех точках области, а только в точках пересечения двух систем равноотстоящих линий, параллельных осям x и y (рис.2). Системы линий называют сеткой, точки пересечений − узлами сетки, а расстояние между линиями − шагом или делением сетки.

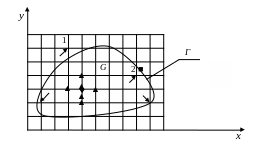
Рис. 2

Обозначим символом Ω множество узлов, принадлежащих области G или расположенных близко к ее границе Г. Степень «близости» определяется числом, названным в программе «параметр границы». В зависимости от параметра границы тот или иной узел (например, узел 1) может попасть в множество Ω или нет. Этот вопрос еще будет более подробно обсуждаться ниже в п. 4.

Расчет температур проводится далее только для множества Ω. Значения температуры в узлах теперь удобно обозначить символами T_i,j, где i − номер вертикальной, а j − горизонтальной линии сетки, на пересечении которых находится узел.

Назовем два узла соседними, если они отстоят друг от друга по оси x или y на один шаг сетки. Узлы, у которых все четыре соседних принадлежат Ω, назовем внутренними. Один из внутренних узлов отмечен на рис.2 знаком ♦, а соседние по отношению к нему – знаками ▲. Узлы, у которых хотя бы один соседний не принадлежит Ω, назовем граничными. Некоторые из таких узлов указаны на рис.2 стрелками. Множество всех входящих в Ω узлов называют сеточной областью, а множество граничных узлов – границей сеточной области.

Согласно методу сеток значения температуры в граничных узлах определяются через посредство граничных условий. В программе условия в узле считаются такими же, как в ближайшей к нему из группы выделенных на границе Г точек (ниже в п. 3 и далее они именуются опорными). Как говорят, производится «снос граничных условий». Например, в граничный узел 2 снос может быть произведен из точки, обозначенной знаком ■.

Для внутренних узлов в методе сеток вместо уравнения (1) получается система линейных алгебраических уравнений вида

. (8)

В левой части каждого такого уравнения стоит температура одного из внутренних узлов, а в правой − одна четверть от суммы температур четырех соседних узлов (т.е. средняя температура в соседних узлах). Количество уравнений в этой системе равно числу внутренних узлов. Принимая во внимание граничные условия, можно показать, что количество неизвестных также равно этому числу.

Систему можно решать любым численным методом, например методом Гаусса. Однако, учитывая специальный вид уравнений (8), предпочтительнее оказывается реализованный в программе метод последовательных приближений, использующий рекуррентную формулу вида

. (9)

Здесь n − номер шага процедуры последовательных приближений. Стартовые значения могут быть любыми (сходимость процедуры доказана). Рационально, конечно, выбирать их по возможности близкими к ожидаемому результату.

По мере накопления шагов процедуры результаты предыдущего и последующего шага сближаются. Когда максимальная среди различных узлов разность температур для двух последовательных шагов становится меньше заданного порогового значения, процедура вычислений останавливается, и в качестве окончательных берутся результаты последнего шага. В программе пороговое значение можно выбирать; оно названо «допустимая погрешность приближений».