Федеральное агентство по образованию

___________________________________

Санкт-Петербургский государственный

Электротехнический университет «ЛЭТИ»

_______________________________________

Теория функций комплексной переменной

Методические указания

к практическим занятиям

по высшей математике

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

2010

УДК 512.64(07)

ТФКП: Методические указания к решению задач / сост.: В.Г.Дюмин, А.М.Коточигов, Н.Н.Сосновский.СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2010. 32с.

Содержат примеры решения основных типов задач ТФКП, ориентированных на выполнение заданий, формирующих оценку текущего контроля по этой дисциплине. Предназначены для студентов ФКТИ всех специальностей.

Утверждено

редакционно-издательским советом университета

в качестве методических указаний

© СПбГЭТУ «ЛЭТИ», 2010

Функции комплексного переменного ,, в общем случае отличаются от отображений вещественной плоскостив себятолько формой записи. Важным и чрезвычайно полезным объектом оказывается класс функции комплексного переменного,

имеющих производную такую же, как и функции одной переменной. Известно, что функции нескольких переменных могут иметь частные производные и производные по направлению, но, как правило, производные по разным направлениям не совпадают, и говорить о производной в точке не возможно. Однако для функций комплексной переменной удается описать условия, при которых они допускают дифференцирование. Изучение свойств дифференцируемых функций комплексного переменного составляет содержании методических указаний. Указания ориентированны на демонстрацию того, как свойства таких функций могут быть использованы для решения разнообразных задач. Успешное освоение, излагаемого материала невозможно без элементарных навыков вычислений с комплексными числами и знакомства с простейшими геометрическими объектами, определяемыми в терминах неравенств, связывающих вещественную и мнимую часть комплексного числа, а так же его модуль и аргумент. Краткое изложение всех необходимых для этого сведений можно найти в методических указаниях [1].

Стандартный аппарат математического анализа: пределы, производные, интегралы, ряды широко используется в тексте методических указаний. Там, где эти понятия имеют свою специфику, по сравнению с функциями одной переменной, приведены соответствующие пояснения, но в большинстве случаев достаточно разделить вещественную и мнимую часть и применить к ним стандартный аппарат вещественного анализа.

1. Элементарные функции комплексного переменного

Обсуждение условий дифференцируемости функций комплексного переменного, естественно начать с выяснения того, какие элементарные функции обладают этим свойством. Из очевидного соотношения

Вытекает дифференцируемость любого многочлена. И, поскольку, степенной ряд можно дифференцировать почленно внутри круга его сходимости,

то любая функция дифференцируема в точках, в окрестности которых ее можно разложить в ряд Тейлора. Это достаточное условие, но, как вскоре выясниться, оно является и необходимым. Исследование функций одной переменной по производной удобно поддерживать, контролируя поведение графика функции. Для функций комплексного переменного такой возможности нет. Точки графика лежат в пространстве размерности 4, .

Тем не менее, некоторое графическое представление о функции можно получить, рассматривая образы достаточно простых множеств комплексной плоскости , возникающие под воздействием заданной функции. Для примера, рассмотрим, с этой точки зрения несколько простых функций.

Линейная функция

Эта простая функции очень важна, тек как любая дифференцируемая функция локально похожа на линейную. Рассмотрим действие функции с максимальной подробностью

здесь -- модуль комплексного числаи-- его аргумент. Таким образом, линейная функция осуществляет растяжение, поворот и сдвиг. Следовательно, линейное отображение переводит любое множество в подобное множество. В частности, под воздействием линейного отображения прямые переходят в прямые, а окружности в окружности.

Функция

Эта функция -- следующая по сложности за линейной. Трудно ожидать, что она переведет любую прямую в прямую, а окружность в окружность, простые примеры показывают, что этого не происходит, тем не менее, можно показать, что эта функция переводит множество всех прямых и окружностей в себя. Чтобы убедится в этом, удобно перейти к вещественному (координатному) описанию отображения

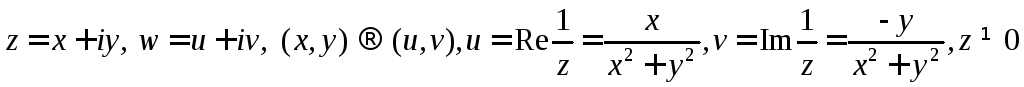
Для доказательства потребуется описание обратного отображения

Рассмотрим уравнение если, то получится общее уравнение прямой. Если, то

Следовательно, при получается уравнение произвольной окружности.

Отметим, что если и, то окружность проходит через начало координат. Если жеи, то получится прямая, проходящая через начало координат.

Под действие инверсии рассматриваемое уравнение перепишется в виде

, ()

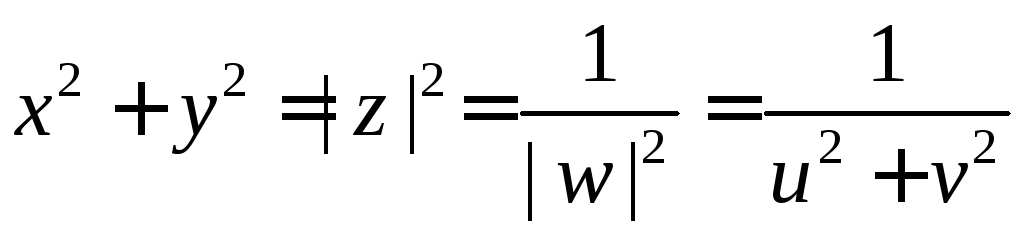или . Видно, что это тоже уравнение, описывающие либо окружности, либо прямые. То, что в уравнении коэффициентыипоменялись местами, означает, что при инверсии прямые, проходящие через 0, перейдут в окружности, а окружности, проходящие через 0, перейдут в прямые.

Степенные функции

Главное отличие этих функцией от рассмотренных ранее состоит в том, что они не являются взаимно однозначными (). Можно сказать, что функцияпереводит комплексную плоскость в два экземпляра той же плоскости. Аккуратное рассмотрение этой темы требует использования громоздкого аппарата римановых поверхностей и выходит за рамки рассматриваемых здесь вопросов. Важно понимать, что комплексную плоскость можно разделить на секторы, каждый из которых взаимно однозначно отображается на комплексную плоскость. Это разбиение для функциивыглядит так,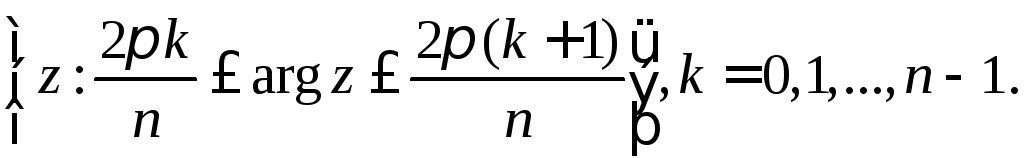Например, верхняя полуплоскость взаимно однозначно отображается на комплексную плоскость функцией. Искажения геометрии для таких изображений описать сложнее, чем в случае инверсии. В качестве упражнения можно проследить, во что переходит сетка прямоугольных координат верхней полуплоскости при отображении

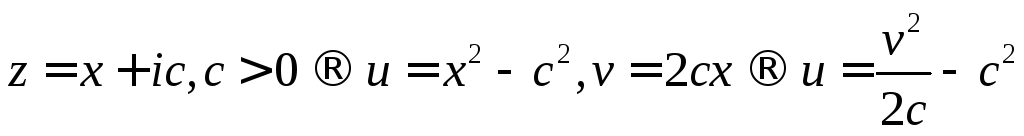
Видно, что сетка прямоугольных координат переходит в семейство парабол, образующих систему криволинейных координат в плоскости . Описанное выше разбиение плоскости таково, что функцияотображает каждый изсекторов на всю плоскость. Описание прямого и обратного отображения выглядит так

Таким образом, функция имеетразличных обратных функций,

заданных в различных секторах плоскости

В таких случаях говорят, что отображение многолистно.

Функция Жуковского

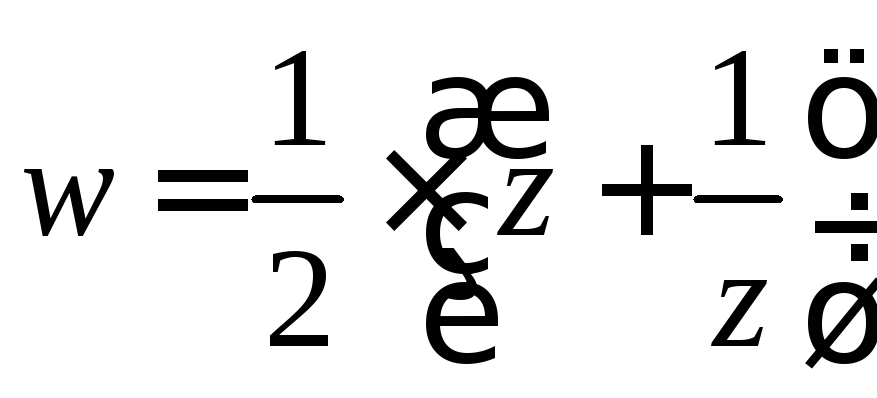
Функция имеет собственное названия, поскольку она составила основу теории крыла летательного аппарата, созданную Жуковским (описание этой конструкции можно найти в книге [2]). Функция обладает рядом интересных свойств, остановимся на одном из них – выясним, на каких множествах эта функция действует взаимнооднозначно. Рассмотрим равенство

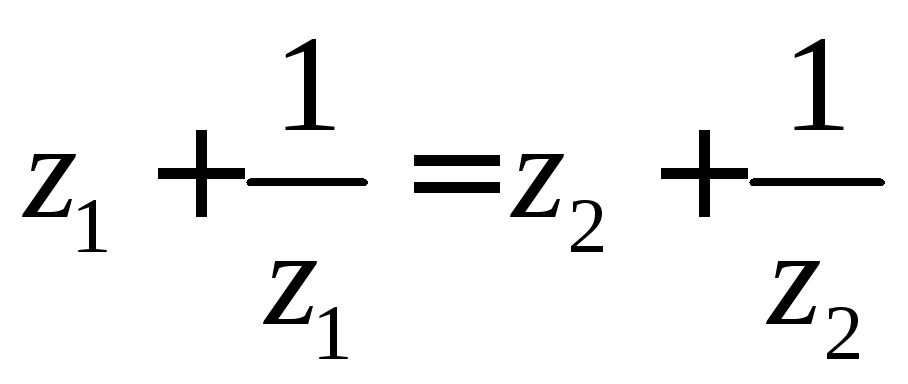, откуда .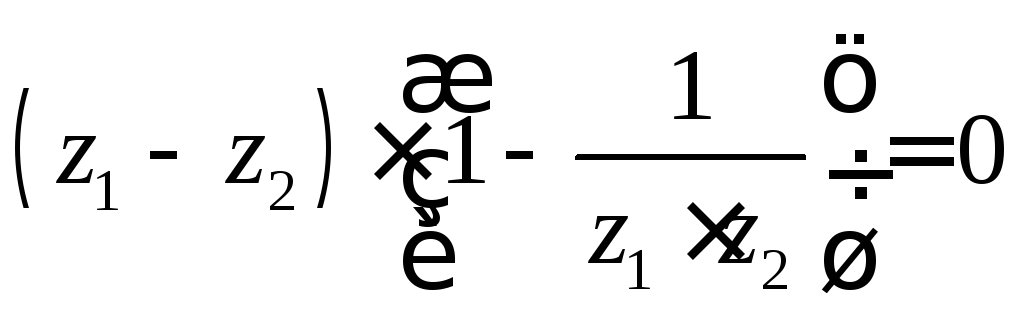

Следовательно, функция Жуковского взаимнооднозначна в любой области, в которой для любых иих произведение не равно единице. Таковыми являются, например, открытый единичный круги дополнение замкнутого единичного круга.

Рассмотрим действие функции Жуковского на окружности , тогда

.

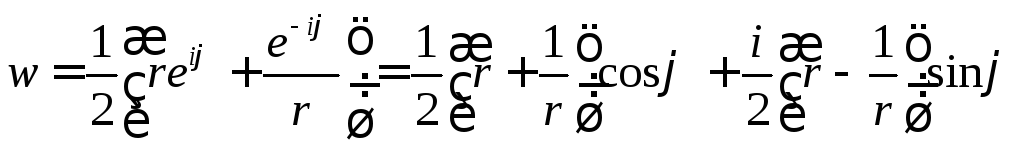Разделяя вещественную и мнимую части, получим параметрическое уравнение эллипса

,.

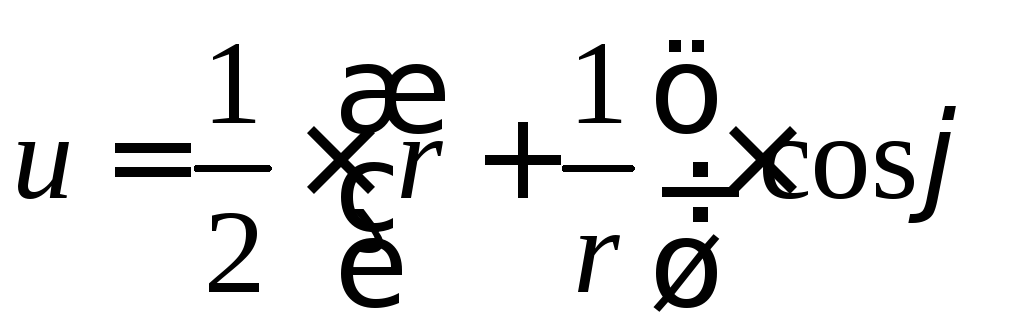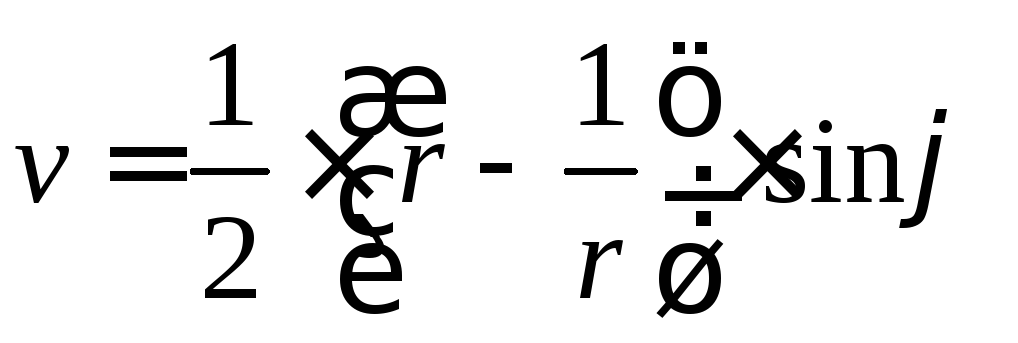Если , то эти эллипсы заполняют всю плоскость. Аналогично проверяется, что образами отрезковявляются гиперболы

.

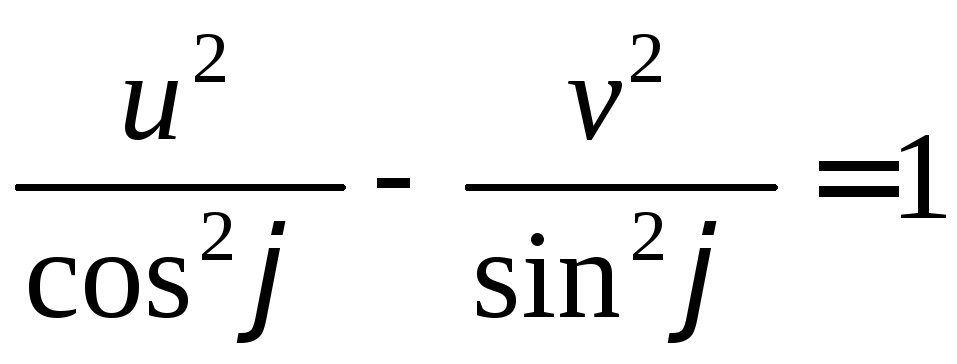Показательная функция

Функция допускает разложение в степенной ряд, абсолютно сходящийся во всей комплексной плоскости, следовательно, она всюду дифференцируема. Опишем множества, на которых функция взаимнооднозначна. Очевидное равенство показывает, что плоскость можно разбить на семейство полос, каждую из которых функция взаимнооднозначно отображает на всю комплексную плоскость. Это разбиение существенно для того, что бы понять, как устроена обратная функция, точнее обратные функции. На каждой из полос естественным образом определено обратное отображение

Обратная функция и в этом случае многолистна, причем количество обратных функций бесконечно.

Геометрическое описание отображения довольно простое: прямые переходят в лучи, отрезкипереходят в окружности.