
Мищенко А. М. Лекции по электротехнике
.pdf
Проанализируем резонансные явления в контуре методом комплексных амплитуд. Комплексное сопротивление контура
Z ( jω) = R + jωL + |
|
|
R1 |
|
|
|
|
|
|
||||||
|
|
= |
|
|
|
|
|
|
|||||||
1 + jωCR |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
= R + 1 |
R |
+ j |
ωL +ωCR 2 (ω2CL −1) |
= |
(4.1.8) |
||||||||||
+ (ωCR )2 |
|
1 + (ωCR )2 |
|
|
|
||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||
= R + |
|
|
R1 |
+ j |
|
ωL +ω3C2 R12 L |
− j |
|
|
ωCR12 |
. |
||||
1 |
+ (ωCR )2 |
1 + (ωCR )2 |
1 |
+ (ωCR )2 |
|||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|||
Первые два слагаемых в уравнении (4.1.8) можно рассматривать как эффективное сопротивление контура, а два последних – как соответственно сопротивления эффективной индуктивности и емкости. Возникновение резонанса будет происходить при частоте
ω = |
1 |
1 − |
L |
|
=ω |
0 |
1 − |
ρ2 |
, |
(4.1.9) |
|
LC |
CR |
2 |
R 2 |
||||||||
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
обеспечивающей выполнение условия Im Z ( jω) = 0 . При этой частоте ток и ЭДС источника находятся в фазе и величина тока максимальна.
Отметим, |
что колебания в контуре возникают лишь при условии |
ρ / R1 < 1, |
когда резонансная частота вещественна. Невыполнение |
этого условия исключает возникновение колебаний (см. эту задачу
ниже, в 4.1.2). При |
ρ / R1 |
<< 1 |
резонансная |
частота ω ≈ ω0, а |
|||
комплексное сопротивление в окрестности ω0: |
|
||||||
Z ( jω) ≈ R + R |
ρ2 |
|
+ jωL + |
1 |
, |
(4.1.10) |
|
|
|
jωC |
|||||
1 R 2 |
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
т. е. оно соответствует простому последовательному контуру с
эффективным сопротивлением |
R |
= R + R ρ2 |
/ R 2 |
и с такими же |
|
эф |
1 |
1 |
|
емкостью и индуктивностью, как в исходном контуре. Поэтому добротность контура легко находится как
Q ≈ |
ρ |
= |
ρ |
|
. |
(4.1.11) |
|
R + R1 ρ2 |
/ R12 |
||||
|
Rэф |
|
|
|||
Наличие шунтирующего емкость сопротивления R1 сказывается тем |
||||||
меньше, чем лучше выполняется неравенство |
ρ / R1 << 1. Отметим, |
|||||
что это решение корректно при наличии большой добротности не менее ≈ 102.
61
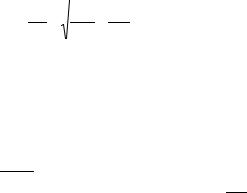
4.1.2*. Физический способ определения параметров контура
Физический способ определения параметров контура основан на рассмотрении колебательных процессов в контуре. Найдем собственные колебания тока в простом последовательном контуре. Такие колебания будут возникать, если, например, зарядить емкость, а затем выходы контура замкнуть. Иначе говоря, в начальный момент времени (t = 0) напряжение на конденсаторе равно uc(0), а весь контур состоит из цепи с последовательным соединением емкости, индуктивности и сопротивления. По закону напряжений Кирхгофа
|
L di |
+ Ri + |
1 t |
|
idt +uc (0) = 0 . |
(4.1.12) |
|||||||
|
|
|
|
||||||||||
C ∫ |
|||||||||||||
|
dt |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
||
Дифференцируя (4.1.12), получаем уравнение |
|
||||||||||||
|
d 2i |
|
+ |
R di |
+ |
|
|
1 |
i = 0 , |
(4.1.13) |
|||
|
|
|
|
|
|
|
|
|
|||||
|
dt 2 |
|
L dt |
|
LC |
||||||||
|
|
|
|
|
|
||||||||
описывающее изменение тока со временем. Уравнение (4.1.12) является обычным однородным дифференциальным уравнением, описывающим затухающие колебания. Решение этого уравнения ищут в виде
|
i(t) = I e p1t |
+ I |
2 |
e p2t , |
|
|
(4.1.14) |
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
p |
= − |
R |
± |
|
|
R2 |
− |
1 |
, |
– корни характеристического уравнения |
|||
|
1,2 |
|
|
|
2L |
|
|
|
|
4L2 |
|
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p2 + |
R |
p + |
1 |
|
|
= 0 , |
|
|
(4.1.15) |
||||
|
|
|
CL |
|
|
|||||||||
|
|
|
L |
|
|
|
|
|
|
|
||||
а |
I1, |
I2 – константы, |
определяемые из начальных условий. В |
|||||||||||
рассматриваемом случае в первый момент t = 0 ток равен нулю i(0) = 0 .
Физику этого начального условия рассмотрим подробно в § 5. Тогда из уравнения (4.1.12) получаем начальное условие на производную от тока:
dtdi = − ucL(0) При отсутствии диссипации энергии (R = 0) колебания тока
не затухают и имеют частоту ω0 =1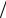

 LC , которая называется
LC , которая называется
собственной частотой контура. Наоборот, при значительной диссипации энергии за период собственных колебаний (R/2L > ω0) ток в контуре не совершает никаких колебаний, а лишь экспоненциально затухает. Такое затухание колебаний называют апериодическим. В промежуточном случае слабого затухания (R/2L < ω0) величина тока экспоненциально падает, совершая при этом периодические колебания
62

|
|
i(t) = Im exp(−δt) cos(ω1t +ϕ) . |
(4.1.16) |
|||
|
|
|
|
|||
Здесь δ = R/2L, |
ω = ω2 −δ 2 |
, а Im и ϕ – постоянные интегрирования, |
||||
|
1 |
0 |
|
|
|
|
определяемые |
из |
начальных |
условий. |
В рассматриваемом |
случае |
|
Im = uc (0) ω1L , а ϕ =π / 2 . На рис.4.1.7 |
приведен график расчета тока |
|||||
для случая R=1 Ом, δ = 0,2. |
|
|
|
|||
Рис. 4.1.7
В электронике особую важность представляют колебания со слабым затуханием (R/2L << ω0). Для описания их и контуров, в которых они реализуются, используют следующие характеристики.
1. Декремент затухания δ = R/2L. Обратная величина от декремента соответствует времени τ = 1/δ, за которое амплитуда колебаний
уменьшится в e раз.
2. Логарифмический декремент затухания
δl = ln |
|
i(t) |
=δ T , |
(4.1.17) |
||||||
i(t +T ) |
||||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
где T =T |
|
1−(δ ω |
0 |
)2 |
– период затухающих колебаний, T = 2π ω |
0 |
– |
|||
0 |
|
|
|
|
|
0 |
|
|||
период собственных колебаний. Физический смысл логарифмического декремента вытекает из определения количества колебаний N, совершенных за время падения амплитуды колебаний в e раз. Величина N =τ T =1
T =1 (δT ) . Поэтому, логарифмический декремент это обратная
(δT ) . Поэтому, логарифмический декремент это обратная
величина от N: δ =1 N . |
|
3. Добротность колебательного контура |
|
Q =π /δl =π N . |
(4.1.18) |
Добротность контура тем больше, чем меньше затухание или чем большее число колебаний произойдет в контуре за время падения
амплитуды в e раз. Введение численного множителя π сделано для совпадения величины данной добротности и добротности определяемой по ширине резонансных максимумов (4.1.7).
63

Добротность контура можно определить и через энергетические потери в контуре:
Q = 2π |
∑W |
=ω |
∑W |
, |
(4.1.19) |
|
|
||||
|
P T |
1 |
|
|
|
|
|
P |
|
|
|
где W – энергия, запасенная в контуре; P – мощность потерь в контуре при свободных колебаниях, Т – период затухающих колебаний.
В рассматриваемом последовательном контуре при условии δ << ω0 имеем
|
δ2π |
|
|
|
|
=πR |
|
, Q =( 1 |
|
|
L |
|
|
ρ |
|
|
δl ≈ |
ω0 |
=πR |
C |
L |
ρ |
R |
) |
C |
= |
, |
(4.1.20) |
|||||
|
|
|
|
|
|
|
|
|
R |
|
|
|||||
где ρ = L / C |
– характеристическое, или |
волновое, |
сопротивление |
|||||||||||||
контура. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4.1.2. В качестве примера проанализируем работу схемы, приведенной на рис. 4.1.6. Рассмотрим собственные колебания в контуре при коротко замкнутом источнике. Для такого контура (E = 0) уравнения Кирхгофа
|
Ri 1 |
+ L |
di |
1 |
|
+ R1 i2 = 0 , |
|
||
|
|
|
|
||||||
dt |
|
|
|
||||||
|
|
1 |
t |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
R1 i2 − |
|
|
|
i3 dt |
− u C ( 0 ) = 0 , |
(4.1.21) |
|||
|
C ∫0 |
||||||||
|
|
|
|
|
|
|
|
||
|
|
|
i1 − i2 − i3 = 0 , |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где i1, i2 и i3 - соответственно, токи в сопротивлении R, R1 и емкости, uC(0)
– начальное напряжение на емкости. Дифференцируя второе уравнение и осуществляя замену i3, получаем систему
|
Ri |
+ L di1 + R i |
= 0, |
|
||||||
|
1 |
|
|
dt |
1 2 |
|
|
(4.1.22) |
||
|
1 |
|
1 |
|
di |
|
|
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
C i1 |
− C i2 − R1 dt |
= 0. |
|
|||||||
Заменяя d / dt |
на p, находим характеристическое уравнение |
|
||||||||
R CLp2 +(R RC + L) p + R + R =0 . |
(4.1.23) |
|||||||||
|
1 |
|
|
|
1 |
|
|
1 |
|
|
Корни этого уравнения
64

p |
= − |
ω |
0 (R + R |
|
ρ2 |
) ± jω |
|
1−(R − R |
|
|
ρ2 |
)2 |
|
ρ2 . |
|
|
|
|
|
(4.1.24) |
||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1,2 |
|
|
ρ |
1 R |
|
|
|
|
|
1 R 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Собственные |
|
колебания |
|
с |
частотой ω =ω |
|
|
|
|
1− |
(R − R |
|
ρ2 |
)2 |
ρ2 |
|||||||||||||||||||
|
|
0 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
R 2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
возникают в контуре при положительном подкоренном выражении. |
||||||||||||||||||||||||||||||||||
Добротность контура |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Q =π |
|
|
|
1 |
|
|
|
|
|
|
|
≈π |
|
|
1 |
|
|
|
|
|
|
|
|
|
= |
ρ |
|
|
. (4.1.25) |
|||||
ω |
|
(R + R |
ρ2 |
)T |
ω |
(R + R |
ρ2 |
|
|
2π |
R + R |
|
ρ2 |
|||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
R 2 |
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2ρ |
|
1 |
|
|
|
|
|
2ρ |
1 R 2 |
|
|
0 |
|
|
|
1 R |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
Отметим, что, для того чтобы частота свободных колебаний приблизительно равнялась собственной частоте ω0, кроме ρ / R1 << 1, необходимо R / ρ << 1 . Одновременное выполнение этих неравенств возможно, лишь при R << R1.
Резонансные явления в стационарном режиме в цепи с подключенным источником напряжения и собственные колебания определяются только свойствами самой цепи, поэтому не случайно добротность, собственная и резонансная частота совпадают для цепей с малой величиной диссипации энергии.
4.2. Параллельный колебательный контур. Резонанс токов
4.2.1. Метод комплексных амплитуд определения параметров контура
Метод комплексных амплитуд определения параметров параллельного контура основан на расчете его комплексной проводимости. Рассмотрим простую цепь, состоящую из параллельно соединенных индуктивности, емкости и сопротивления. Подключим эту цепь к идеальному источнику
синусоидального тока I (t) = Im sin(ωt +ψ) . В результате получается
схема, показанная рис. 4.2.1. Поэтому цепь называют параллельным колебательным контуром. Найдем стационарное напряжение на контуре методом комплексных амплитуд. Согласно закону Ома:
Imejψ =Y( jω)U =(R1 + jω1L + jωC)U = 
, (4.2.1)
где Y – комплексная проводимость цепи, Um – амплитуда напряжения, ψ0 и

ψ1 – аргумент комплексной проводимости и фаза напряжения. Мгновенное значение напряжение на контуре
u(t) =Um sin(ωt +ψ1) , |
|
(4.2.2) |
|
|
|
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Um |
= |
I0m |
|
|
= = |
I0m R |
|
|
|
= |
I0m R |
, |
|||
|
1 |
|
|
|
ω |
|
ω0 |
|
1 +Q2 x2 |
||||||
|
1 |
+ (ωC − |
2 |
|
2 |
|
|
|
2 |
|
|||||
|
R2 |
ωL) |
|
|
1 +Q |
( |
|
|
− |
|
) |
|
|
|
|
|
|
|
ω0 |
ω |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(4.2.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а сдвиг фазы между напряжением и током, равный аргументу комплексной проводимости (ψ1 −ψ =ψ0 ):
tg(ψ1 −ψ) = −R(ωC −1/ωL) = −Qx . |
(4.2.4) |
В выражениях (4.2.3) и (4.2.4) введены следующие параметры:
Q = |
R |
= R |
ρ |
(4.2.5) |
|
L C |
|
|
|
– добротность |
параллельного контура, а |
x = (ω ω0 −ω0 ω) – |
||
относительная расстройка и ω0 =1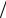

 LC – собственная частота контура.
LC – собственная частота контура.
Видно, что частотная зависимость амплитуды напряжения (АЧХ) на параллельном контуре аналогична частотной зависимости тока в последовательном контуре: максимальное, резонансное значение
амплитуды напряжения на контуре Um0 = Im R достигается при ω = ω0;
максимум Um тем выше и острее, чем больше добротность контура. Поэтому все рассуждения о полуширине спектра и связи ее с добротностью справедливы и в этом случае. Однако из формулы 4.2.5 следует, что в данном контуре с увеличением сопротивления добротность возрастает, а полоса пропускания уменьшается. Поэтому во избежание расширения полосы пропускания контура необходимо использовать источники тока с внутренним сопротивлением больше, чем у контура. Тогда проводимость нагруженного контура, являющаяся суммой проводимостей источника тока Y0 и ненагруженного контура Y, не будет сильно отличаться от величины Y. При соединении параллельного контура к источнику напряжения анализ напряжения на контуре проще проводить,
если источник напряжения |
заменить |
эквивалентным источникам тока. |
ω = ω0 |
При резонансной частоте |
разность фаз ψ0 = ψ – ψ1 между втекающим
66
в контур током и напряжением на нем равна нулю. Это позволяет наиболее просто определять резонансную частоту напряжения на контуре из условия равенства нулю реактивной части полной комплексной проводимости контура ImY ( jω) = 0 . Для рассматриваемого контура, где
комплексная |
проводимость |
Y = 1/ R +1/ jωL + jωC , |
сразу |
следует |
|||||
ω0 =1 |
|
. |
|
|
|
|
|||
LC |
При этом непосредственно |
получается |
и |
резонансная |
|||||
амплитуда напряжения |
Umo = Im R . Токи |
при резонансе |
в |
емкости |
|||||
IC =Um0 jωC = jI0mQ |
и в |
индуктивности IL =Um0 / jωL = − jI0mQ |
|||||||
равны и противоположны по направлению. Поэтому о резонансе в параллельных контурах принято говорить как о резонансе токов. Диаграмма токов при резонансе показана на рис. 4.2.2. Тем не менее, хотя величины токов в емкости и индуктивности при ω = ω0 в Q раз больше втекающего тока, они не максимальны. Максимальная амплитуда тока в
емкости достигается при ωC = ω0 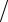

 1 −1
1 −1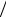 2Q2 , а в индуктивности – при
2Q2 , а в индуктивности – при
ωL = ω0  1 −1 2Q2 . Поэтому частоты ωC и ωL также можно считать резонансными. Однако в радиотехнике их не считают резонансными, так как они не удовлетворяют условию ImY ( jω0 ) = 0 . Это связано с тем, что
1 −1 2Q2 . Поэтому частоты ωC и ωL также можно считать резонансными. Однако в радиотехнике их не считают резонансными, так как они не удовлетворяют условию ImY ( jω0 ) = 0 . Это связано с тем, что
из-за использования в радиотехнике контуров с большой добротностью вообще не возникает потребности в выделении данных частот, так как практически нет разницы между ωC и ωL или ω0. Например, при Q = 100
частоты ωC и ωL отличаются от ω0 всего на ≈ 2 10−3 % . Амплитудночастотные характеристики (АЧХ) тока в конденсаторе соответствуют АЧХ напряжения на индуктивности, а АЧХ тока в индуктивности соответствует амплитудно-частотной характеристике напряжения на емкости в последовательном контуре (см. рис. 4.1..4).
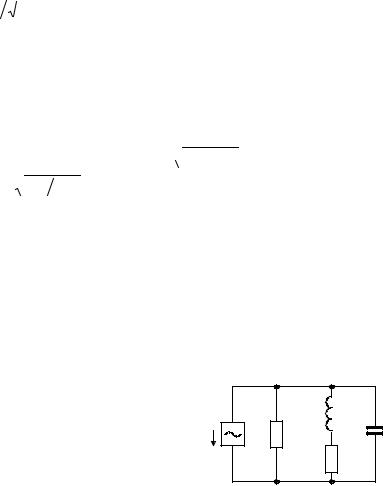
Пример 4.2.1. Рассмотрим |
|
параллельный контур, изображенный |
|
на рис. 4.2.4 Источник тока I0 с |
I0 |
внутренним сопротивлением R0 |
|
питает колебательный контур, |
|
состоящий из индуктивности L с |
|
потерями, представленными |
|
последовательно включенным |
|
сопротивлением R, и емкости C. |
|
Найдем резонансную частоту и |
|
добротность контура. |
|
|
L |
R0 |
C |
|
R |
|
Рис. 4.2.4 |
В этом контуре ветви, содержащие емкость и индуктивность, параллельны и параллельно присоединены к источнику. Поэтому контур
67
является параллельным колебательным контуром. Решение проведем методом комплексных амплитуд. Комплексная проводимость контура
Y ( jω) = |
1 |
|
+ jωC |
+ |
|
|
1 |
|
= |
1 |
+ |
|
|
R |
|
|
+ |
||||||||||
|
R |
|
R |
+ jωL |
|
R |
R2 |
+ (ωL)2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
+ j |
ω3L2C + R2ωC −ωL |
= |
1 |
|
+ |
|
|
1 |
|
|
|
+ |
|
||||||||||||||
|
|
|
R |
|
|
|
|
|
ω2 |
|
ρ2 |
|
|
||||||||||||||
|
|
|
R2 + (ωL)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
R(1 + ω02 |
|
|
) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|||||
+ j |
ω2 |
|
|
|
|
|
ρ |
|
|
|
|
|
( |
ω2 |
+ |
R2 |
|
−1) , |
|
|
|
|
(4.2.6) |
||||
ω2 |
|
R2 |
(1 + |
ω2 |
|
ρ2 |
) |
|
ω2 |
ρ2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ω02 |
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где ρ = |
L / C , ω0 |
=1/ |
|
|
LC . |
|
Резонансная |
частота находится из |
|||||||||||||||||||
равенства нулю мнимой части проводимости. Исключая случай
постоянного тока (ω = 0), резонанс в контуре может возникнуть при |
|||||
R / ρ < 1 c частотой ω |
p |
=ω |
0 |
1 − R / ρ2 |
. При R / ρ << 1 выражение для |
|
|
1 |
|
||
проводимости контура упрощается: |
|
||||
|
1 |
|
ω2 |
R |
|
ω |
1 |
|
ω2 |
|
1 |
|
ω2 |
R |
|
1 |
|
Y( jω) ≈ |
|
+ |
|
|
+ j |
0 |
|
( |
|
−1) ≈ |
|
+ |
|
|
+ j(ωC − |
|
) , (4.2.7) |
R |
ω2 |
ρ2 |
|
ω2 |
R |
ω2 |
ρ2 |
ωL |
|||||||||
|
|
|
ω ρ |
|
|
|
|
|
|||||||||
|
0 |
|
0 |
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
приобретая вид, соответствующий контуру с идеальными элементами, но
|
|
|
|
|
|
|
|
|
ω2 |
|
ρ2 |
|
шунтированным сопротивлением |
R = |
0 |
|
|
(Сопротивления R0 и R1 |
|||||||
|
R |
|||||||||||
|
|
|
|
|
|
|
|
1 |
ω2 |
|
|
|
соединены параллельно). В силу сделанного предположения ( R / ρ << 1) |
||||||||||||
вблизи резонансной частоты R ≈ ρ2 / R и добротность такого контура |
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
R |
|
R |
|
R R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Q = |
0 |
|
1 |
= |
0 |
1 |
. При |
R0 > R1 |
источник тока не влияет на |
|||
|
|
|
|
|
||||||||
|
ρ |
(R0 + R1 )ρ |
||||||||||
|
|
|
|
|
|
|
|
|
||||
добротность ( Q ≈ R1 / ρ = ρ / R ) и на колебательные процессы в контуре.
Добротность становится равной добротности последовательного контура, состоящего из индуктивности L емкости C и сопротивления R. При
R0 < R1 добротность контура будет определяться величиной внутреннего сопротивления источника Q ≈ R0 / ρ . Полученное решение корректно при наличии большой добротности не менее ≈ 102.
68
4.2.2*. Физический способ определения параметров
Найдем собственные колебания напряжения на контуре, состоящем из параллельно соединенных емкости, индуктивности и сопротивления, когда источник отсоединен. Пусть, например, в начальный момент времени (t = 0) ток в индуктивности равен iL(0), а напряжение на емкости u(0) = 0 .
По закону токов Кирхгофа
C du + |
u |
+ |
1 |
t udt +iL (0) = 0 . |
(4.2.7) |
||||||
R |
|
||||||||||
|
dt |
|
|
|
L ∫ |
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
|
Дифференцируя уравнение (4.2.7) по времени, получаем |
|||||||||||
уравнение: |
|
|
|
|
|
|
|
||||
|
d 2u |
+ |
1 |
|
du |
+ |
1 |
u = 0 , |
|
||
|
|
RC dt |
|
|
|||||||
|
dt2 |
|
LC |
|
|||||||
(4.2.8) |
|
|
|
|
|
|
|
|
|
|
|
описывающее изменение напряжения на контуре. Уравнение (4.2.8) подобно уравнению (4.1.13). Оно является однородным дифференциальным уравнением, описывающим собственные затухающие колебания. При отсутствии потерь энергии в контуре ( R = ∞ , т. е. разорвать цепь с сопротивлением) напряжение будет соответствовать периодическим незатухающим колебаниям с собственной частотой
контура ω0 =1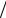

 LC . Если потери энергии за период собственных
LC . Если потери энергии за период собственных
колебаний значительны, то второй член в уравнении (4.2.8) доминирует над третьим и напряжение экспоненциально падает, не совершая колебаний. Такое затухание колебаний называют апериодическим. Это наглядно видно из выражения для корней характеристического уравнения
p |
= − 1 |
± |
1 |
− 1 . В промежуточном случае слабых |
|
1,2 |
2RC |
|
4R2C 2 |
LC |
|
|
|
|
|||
затуханий (1/2RC < ω0 подкоренное выражение отрицательно) возникают периодические колебания напряжения с экспоненциальным падением амплитуды.
u(t) =Um exp(−δt)cos(ω1t +ψ) . |
|
|
|
|
|
(4.2.9) |
||||||
В |
выражении |
(4.2.9) δ =1/ 2RC является |
декрементом затухания, |
|||||||||
|
|
|
|
|
|
|
||||||
ω = |
|
ω2 −δ 2 , |
Um и ψ – постоянные интегрирования, определяемые из |
|||||||||
1 |
0 |
|
|
|
|
|
|
|
u(0) = 0 |
|||
начальных условий. (В рассматриваемом случае из |
условия |
|||||||||||
следует ψ = π / 2 , а из (4.2.7) вытекает C du = −i |
L |
(0) |
или U |
m |
= |
iL (0) |
). |
|||||
|
||||||||||||
|
|
|
|
dt |
|
|
|
|
ω C |
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
69 |
||
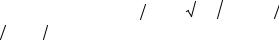
Введем логарифмический декремент аналогично выражению (4.1.17), как
δl = ln |
u(t) |
=δT . Тогда при |
δ <<ω0 логарифмический декремент |
||||
u(t +T ) |
|||||||
|
|
|
|
|
|
||
|
|
δl |
≈δ 2π ω0 =π |
|
RC =πρ R , а |
||
параллельного |
контура будет |
LC |
|||||
добротность Q ≈π δl = R ρ . Еще |
раз подчеркнем, что добротность |
||||||
параллельного контура, в отличие от последовательного, тем больше, чем больше активное сопротивление. В пределе бесконечного сопротивления, равносильного разрыву, энергия, запасенная в индуктивности и емкости, будет последовательно переходить из состояния обусловленного энергией магнитного поля в состояние с энергией электрического поля. Такие переходы будут обеспечивать бесконечные колебания напряжения, следовательно, и бесконечную добротность контура.
Пример 4.2.2. Проанализируем работу схемы, приведенной на рис. 4.2.4, используя дифференциальные уравнения Кирхгофа. Найдем собственные колебания в контуре, когда источник тока отключен, но сопротивление R0 оставлено. Начальным состоянием контура выберем состояние, в котором токи отсутствуют, а конденсатор имеет напряжение uC(0). Систему уравнений Кирхгофа запишем через напряжения на элементах цепи
|
duC |
|
uC |
|
|
|
|
1 t |
||||
C |
|
+ |
|
|
|
+ |
|
|
∫uLdt =0, |
|||
dt |
R |
|
|
L |
||||||||
|
|
|
|
0 |
|
|
|
0 |
||||
|
t |
|
|
u |
|
|
|
|
||||
1 |
∫uLdt = |
R |
, |
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||
L |
0 |
|
|
|
R |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
uL +uR =uC . |
|
|
|
|||||||||
Дифференцируя уравнения и сопротивлении R, получаем систему уравнений
(4.2.10)
исключая напряжение uR на однородных дифференциальных
|
|
d 2uC |
|
1 duC |
|
|
|
1 |
|
|
||||||
C |
|
|
|
+ |
|
|
|
|
|
+ |
|
uL = 0, |
|
|||
|
d 2t |
R |
dt |
|
L |
(4.2.11) |
||||||||||
|
1 |
|
duC |
|
0 |
|
|
|
|
1 |
|
|
||||
|
|
− |
1 duL |
− |
uL = 0, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dt |
R dt |
L |
|
||||||||||
R |
|
|
|
|
|
|
|
|||||||||
которую преобразуем в одно дифференциальное уравнение относительно напряжения на конденсаторе:
70
