
Мищенко А. М. Лекции по электротехнике
.pdf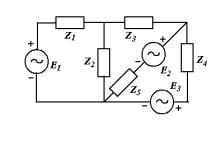
не только симметрична относительно главной диагонали, но в ней все общие сопротивления вошли с отрицательным знаком. Это дает дополнительный контроль правильности составления системы уравнений. Во многих случаях для сравнительно простых схем независимые контуры могут быть найдены без применения общих методов, а лишь на основании известного их числа.
Пример 3.1.1. Запишем в качестве примера уравнения Кирхгофа для контурных токов для цепи приведенной на рис. 3.1.2. для двух случаев: 1) случай не перекрывающихся контуров, 2) случай смешанных контуров (часть перекрываются, а часть нет).
Первый случай. Найдем независимые не перекрывающиеся контуры первым способом. Деревом схемы являются ветви cодержащие сопротивления Z2 и Z5 и выходящие из нижнего узла. Подсоединение ветви с сопротивлением Z1 образует первый контур, подсоединение ветви
Рис. 3.1.2 с сопротивлением Z3 – второй контур, а присоединение ветви с сопротивлением Z4 – третий контур. Все контурные токи положим
текущими по часовой стрелке. Тогда каноническая система уравнений имеет вид:
E |
|
=(Z |
|
+Z |
2 |
)I |
1 |
−Z |
2 |
I |
2 |
+ |
0I |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
−E2 = −Z2 I1 +(Z2 +Z3 +Z5 )I2 −Z5 I3 , |
|
|
|
|
(3.1.7) |
||||||||||||||||||||||||||||
E |
2 |
−E |
|
=0I |
1 |
−Z |
5 |
I |
2 |
+(Z |
4 |
+Z |
5 |
)I |
3 |
|
|
|
|
|
|
|
|||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а ее матричный – вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
E |
|
(Z |
|
+ |
Z |
2 |
) − Z |
2 |
|
|
|
|
0 |
|
I |
1 |
|
|
|||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− Z4 |
|
|
|
||||||||
− E2 |
|
= |
− Z2 |
|
|
|
(Z2 + Z3 + Z5 ) |
I2 |
|
(3.1.7 а) |
|||||||||||||||||||||||
E |
2 |
− E |
|
|
|
0 |
|
|
|
|
|
|
− Z |
4 |
|
|
(Z |
4 |
+ Z |
5 |
) I |
3 |
|
|
|||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Видно, что матрица сопротивлений имеет симметрию относительно главной диагонали и что сопротивления, принадлежащие разным контурам, входят со знаком минус.
Второй случай. Найдем независимые контуры вторым способом. В качестве исходного контура возьмем контур состоящий из ветвей с источниками ЭДС Е1 и Е2 и ветви с сопротивлением Z3. Разомкнем ветвь с Е1 и возьмем в качестве второго контура замкнутый контур из ветвей, содержащих сопротивления Z2, Z3 и Z5. Отсоединим ветвь с сопротивлением Z3, оставшийся последний контур будет третьим.
41

Дальнейшее размыкание (отсоединение) ветвей приведет к отсутствию замкнутых контуров. Пусть все токи имеют направление по часовой стрелке. Тогда каноническая система уравнения Кирхгофа имеет вид
E |
|
−E |
2 |
=(Z |
+Z |
3 |
+Z |
5 |
)I |
1 |
+Z I |
2 |
−Z |
5 |
I |
3 |
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
E1 = Z1I1 +(Z1 +Z2 )I2 +0I3 |
|
|
|
|
|
|
|
, |
|
|
|
|
(3.1.8) |
||||||||||||||||||||||
E |
2 |
−E |
= −Z |
5 |
I |
1 |
+ |
0I |
2 |
|
+(Z |
4 |
+Z |
5 |
)I |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
или в матричном виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
E |
|
− E |
2 |
|
(Z |
+ |
Z |
3 |
+ Z |
5 |
) |
|
Z |
|
|
|
|
− Z |
5 |
|
I |
1 |
|
||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
E1 |
|
|
= |
|
|
|
|
|
Z1 |
|
|
|
|
|
|
(Z1 + Z2 ) |
|
|
|
|
0 |
|
|
I2 |
. |
||||||||
E |
2 |
− E |
|
|
|
|
− Z |
5 |
|
|
|
|
|
|
|
0 |
|
|
(Z |
4 |
+ Z |
5 |
) I |
3 |
|
||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(3.1.8 а)
Видно, что матрица сопротивлений имеет симметрию относительно главной диагонали. Однако знаки общих сопротивлений зависят от того, являются контуры перекрывающимися или нет. При не перекрывающихся контурах знак минус, а при перекрывающихся контурах знак плюс.
При составлении системы уравнений Кирхгофа для контурных токов предполагалось, что во всех контурах имеются только источники напряжения. При наличии в схеме источников тока их заменяют эквивалентными источниками напряжения или берут в качестве контурных токов токи идеальных источников тока. В последнем случае число уравнений (ранг системы) уменьшается на количество известных
(заданных) контурных |
Z1 |
Z3 |
|
токов. |
|||
|
|
|
Пример |
|
3.1.2. |
|
|
I2 |
|
|
Найдем |
токи в |
ветвях |
|
|
I00 |
|||
схемы, |
изображенной |
E1 |
I1 |
Z2 |
||||
на |
рис. 3.1.3. |
Она |
Z4 |
|||||
состоит |
|
из |
двух |
|
|
|
I3 |
|
идеальных |
источников |
|
|
|
|
|||
напряжения E1, E2; |
|
|
|
E2 |
||||
идеального |
источника |
|
|
|
||||
тока I00 и комплексных |
|
|
Рис. 3.1.4 |
|
||||
сопротивлений |
Z1, Z2, |
|
|
Рис. 3.1.3. |
|
|||
Z3, Z4. Схема имеет пять ветвей и три узла. Число независимых контуров |
||||||||
равно трем. Однако в силу того, что в схеме имеется идеальный источник |
||||||||
тока, для нахождения контурных токов достаточно найти два независимых |
||||||||
контура не содержащих идеальный источник тока. Тогда как в контуре, |
||||||||
содержащем источник тока, контурный ток приравнять току источника. |
||||||||
Будем искать независимые контуры вторым способом. В качестве первого |
||||||||
42
возьмем контур, состоящий из источника тока E1 и комплексных сопротивлений Z1 и Z2. Уберем ветвь с Z1. Тогда следующим (вторым) контуром можно взять любой другой замкнутый контур. Возьмем, например, контур, состоящий из сопротивлений Z2, Z3 и источника тока. В этом случае получить следующий (третий) независимый контур можно лишь размыканием ветви, содержащей идеальный источник тока. Этот контур будет состоять из источника напряжения E2 и сопротивлений Z2, Z3, Z4. Неизвестными контурными токами являются токи I1 и I3 для первого и третьего контура. Во втором контуре контурный ток I2 = I00, и направление его совпадает с направлением тока источника тока. Направления токов I1 и I3 выберем по часовой стрелке. В итоге, уравнения для контурных токов имеют вид
|
E |
=ZI |
+Z (I |
−I −I )=(Z +Z )I |
−Z I −Z I , |
|
|
(3.1.9) |
|||||||||
|
|
1 |
1 1 |
2 |
1 |
00 |
3 |
1 |
2 |
1 |
2 00 |
2 3 |
|
|
|
||
−E2 =−Z2(I1−I00−I3)+Z3(I3 +I00)−Z4I3 =−Z2I1+(Z2 +Z3)I00+(Z2 +Z3 +Z4)I3. |
|
||||||||||||||||
Решение этой системы приводит к выражениям для контурных токов |
|||||||||||||||||
I1 |
= |
|
(Z2 + Z3 + Z4 )E1 − Z2 E2 + Z2 Z4 I00 |
|
, |
|
|
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
(Z1 + Z2 )(Z2 + Z3 + Z4 ) − Z22 |
|
|
|
|
(3.1.10) |
||||||||
|
|
|
|
Z2 E1 − (Z1 + Z2 )E2 −(Z1Z2 + Z1Z3 + Z2 Z3 )I00 |
|
||||||||||||
I3 |
|
= |
|
. |
|
||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
(Z1 + Z2 )(Z2 + Z3 + Z4 ) − Z22 |
|
||||||||||
Реальные токи в сопротивлениях получают из соотношений |
|
||||||||||||||||
IZ1 |
= I1, IZ 2 |
= I1 − I3 − I00 |
, |
|
|
|
|
|
|
(3.1.11) |
|||||||
IZ3 |
= I3 + I00 , IZ 4 |
= I3 |
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
Дальнейшие алгебраические вычисления опустим.
3.2. Метод узловых потенциалов (напряжений)
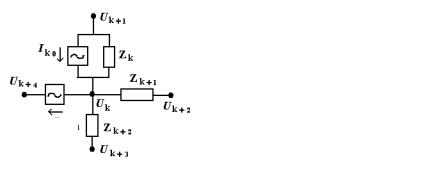
Метод узловых напряжений основан на явном использовании закона токов Кирхгофа. В отличие от метода контурных токов основными неизвестными считают узловые потенциалы. В уравнениях записанных на основании закона токов Кирхгофа токи в ветвях определяются через потенциалы на концах ветвей. На рис. 3.2.1 а изображена часть цепи с пятью ближайшими узлами. Запишем закон тока Кирхгофа для k-го узла, используя закон Ома для ветвей. При этом удобно полагать, что токи втекают в узел. Тогда:
Uk+2 −Uk + Uk+3 −Uk + Uk+1 −(Uk − Ek ) − I0k−1 = 0 . |
(3.2.1) |
||
Zk+1 |
Zk+2 |
Zk |
|
|
|
Рис. 3.2.1 |
|
43
I0k
I0k-1 |
I0k-1 |
а |
б |
Отметим, что закон Ома связывает направление тока в сопротивлении с разностью потенциалов, поэтому можно не задумываться о направлении токов в узлах и для каждого узла, записывая уравнение Кирхгофа, считать токи в сопротивлениях втекающими.
Выражение (3.3.1) удобно преобразовать к каноническому виду
Ek |
−I0k−1 =( |
1 |
+ |
1 |
+ |
1 |
)Uk − |
1 |
Uk+1 − |
1 |
Uk+2 − |
1 |
Uk+3 . (3.2.2) |
Zk |
|
|
Zk+2 |
|
|
|
|||||||
|
Zk |
Zk+1 |
|
Zk |
Zk+1 |
Zk+2 |
|||||||
Это уравнение проще получить, заменив источник напряжения в k-й ветви (сопротивление ветви Zk рассматривается как внутреннее сопротивление
источника ЭДС – Ek) на источник тока: J0k = Ek 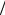 Zk (см. рис. 3.2.1 б).
Zk (см. рис. 3.2.1 б).
Тогда левая часть канонического уравнения является суммой токов источников тока присоединенных к выделенному узлу. Втекающие токи берутся со знаком “+”, а вытекающие – со знаком “–”. Правая часть состоит из слагаемых, где обязательно есть член, являющийся произведением суммы проводимостей ветвей, входящих в выделенный узел (первый член в уравнении (3.2.2)), и его потенциала. Другие члены являются произведением проводимости ветви и потенциала узла, связанного этой ветвью с выделенным узлом. Причем последние члены берутся со знаком “–”.
В общем случае для получения системы уравнений можно следовать двумя путями.
Первый путь – это прямое использование закона Ома и закона токов Кирхгофа для определения токов ветвей. Получаемая система линейно независимых уравнений ранга q-1 состоит из уравнений вида
SI |
SY |
|
∑Iks = ∑Yks (Us −Uks ) s (1, q −1) , |
(3.2.3) |
|
k |
k |
|
44
где суммирование ведется по всем источникам тока (SI) соединенным с узлом s и по всем токам в ветвях (SY) входящих в узел. Ток источников берется со знаком “+”, если он втекает в узел и со знаком “–”, если вытекает. Yks – проводимость ветви, соединяющей узел s с узлом k, имеющим потенциал Uks. При этом не обязательно источники напряжения преобразовывать в источники тока.
Второй путь – это сразу записывать канонические уравнения для q - 1 узлов, предварительно заменив все источники напряжения эквивалентными источниками тока:
I |
01 |
=Y U |
|
−Y U |
|
− −Y |
U |
q −1 |
, |
|
|
|
|||||
|
|
|
|
11 1 |
12 2 |
|
|
1,q−1 |
|
|
|
|
|||||
I02 = −Y21U1 +Y22U2 − −Y2,q−1Uq−1 , |
|
|
|||||||||||||||
.................................................................... |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
0,q −1 |
= −Y |
U |
−Y U |
2 |
−+Y |
|
U |
|
||||||||
|
|
|
|
q−1,1 1 |
|
q−1,2 |
|
|
q−1,q−1 |
q−1 |
|||||||
или в матричном виде |
|
|
|
|
|
|
|
|
|
|
|||||||
I |
01 |
|
|
|
|
Y |
−Y .......... |
|
|
. −Y |
|
|
|
|
|||
|
|
|
11 |
|
12 |
|
|
|
1,q−1 |
U1 |
|||||||
|
I |
|
|
|
−Y |
|
Y |
|
|
−Y |
|
|
|
|
|||
|
02 |
|
|
|
|
|
|
U |
2 |
|
|||||||
|
|
= |
|
21 |
|
22 |
|
|
|
2,q−1 |
|
||||||
... |
|
|
|
........................................... |
... |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I0,q−1 |
|
|
−Y |
−Y |
... −Y |
|
|
Uq−1 |
|
||||||||
|
|
|
|
|
|
|
q−1,1 |
|
q−1,2 |
|
|
q−1,q−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(3.2.4)
(3.2.5)
В выражениях (3.2.4), (3.2.5.) I0i являются алгебраической суммой токов источников тока, присоединенных к узлу i (знак "+" берется для втекающих токов, а знак "-" – для вытекающих). Отметим, что Yki =Yik и
получаемая система симметрична относительно главной диагонали. Если узлы не связаны между собой, то в этом месте в матрице проводимостей ставиться ноль.
Общее решение систем (3.2.5) можно получить методом Крамера
|
1 |
q−1 |
|
|
Uk = |
∑I0i∆ik , |
(3.2.6) |
||
∆ |
||||
|
i =1 |
|
||
|
|
|
где ∆ – определитель системы, ∆ik – алгебраическое дополнение к
элементу Yik.
Метод узловых напряжений при аналитических расчетах имеет преимущество перед методом контурных токов, тогда когда ранг системы (3.2.5) меньше ранга системы (3.2.5), т. е. когда справедливо неравенство q - 1 < p - q + 1 или 2(q - 1) < p . Однако при численных расчетах данные методы равнозначны.
45
Пример 3.2.1. В качестве примера проведем расчет той же самой |
|||||||
схемы (см. рис. 3.1.3), которая использовалась для демонстрации метода |
|||||||
|
|
|
|
|
|
контурных токов. |
|
|
U1 |
Z3 |
U2 |
|
|
Эта схема |
после |
|
|
|
|
|
|
эквивалентной |
|
|
|
|
|
|
|
замены |
|
|
|
|
|
|
|
источников |
|
I01 |
Z1 |
Z2 |
I00 |
Z4 |
I02 |
напряжения |
на |
|
|
|
|
|
|
источники |
тока |
|
0 |
|
|
|
|
I01 = E1 , I02 |
= E2 |
|
|
|
|
|
Z1 |
Z4 |
|
изображена на рис. 3.2.2.
Нижний узел соединения сопротивлений Z1, Z2 и Z4 примем за базовый, в котором потенциал равен нулю. Потенциалы верхних узлов, в которых соединяются сопротивления Z1, Z2, Z3 и сопротивления Z3, Z4, обозначим соответственно U1 и U2. Схема имеет три узла. Поэтому система канонических уравнений, записываемая на основании закона токов Кирхгофа, имеет два уравнения с двумя неизвестными U1 и U2:
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||||
I01 |
= ( |
|
+ |
|
|
|
|
+ |
|
|
|
)U1 |
− |
|
|
|
U2 , |
|||
Z1 |
Z2 |
Z3 |
Z3 |
|||||||||||||||||
|
|
|
|
|
|
|
(3.2.7) |
|||||||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
− I00 = ( Z |
|
|
+ Z |
|
|
)U2 − Z |
|
|
U1. |
|||||||||||
I02 |
3 |
4 |
|
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решая эту систему, получаем напряжения между выделенными узлами и базисным узлом:
U |
1 |
= |
Z1Z2[I01(Z3 + Z4 ) + Z4 (I02 − I00 )] |
, |
|
(3.2.8) |
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
(Z + Z |
2 |
)(Z |
2 |
+ Z |
3 |
+ Z |
4 |
) − Z 2 |
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
U |
2 |
= |
|
Z4Z1[I01Z4 + I00 (Z1Z2 + Z1Z3 + Z2Z3 )] |
. |
(3.2.9) |
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
Z 2 −(Z + Z |
2 |
)(Z |
2 |
+ Z |
3 |
+ Z |
4 |
) |
|
|
||||||||||
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найденные напряжения будут соответствовать аналогичным напряжениям и в исходной схеме. Однако, при определении токов необходимо помнить относительно каких узлов проводилась эквивалентная замена источников напряжения на источники тока. В рассматриваемом случае, только токи в сопротивлениях Z2 и Z3 будут равны в исходной схеме и в схеме изображенной на рис. 3.2.2. Это связано с тем, что эквивалентность замены источника напряжения на источник тока и наоборот понимается по отношению к внешней цепи (см. § 1). Поэтому, для исключения ошибок,
46
определение токов, протекающих в сопротивлениях, проводят на основании закона Ома согласно исходной, непреобразованной схеме.
Токи в сопротивлении Z1 и Z4 |
рассчитываются как |
|
|||||||
I |
Z1 |
= |
E1 −U1 |
, I |
Z 4 |
= |
U2 − E2 |
. |
(3.2.10) |
|
Z4 |
||||||||
|
|
Z1 |
|
|
|
||||
|
|
|
|
|
|
|
|||
Проверьте самостоятельно, что получаемые выражение для этих токов совпадает с выражениями, полученными методом контурных токов.
Токи в сопротивлениях Z2 и Z3 получаем как |
|
||||
I |
Z 2 |
= U1 −0 , I |
Z3 |
= U1 −U2 . |
(3.2.11) |
|
Z2 |
Z3 |
|
||
|
|
|
|
||
При прямом использовании закона Ома для определения токов в ветвях исходной схемы рис. 3.1.5 система уравнений имеет вид (обозначение потенциалов в узлах прежнее)
E |
−U |
1 |
|
|
0 −U |
|
|
U |
|
−U |
|
|
|
||
|
1 |
|
|
+ |
|
|
1 |
+ |
|
2 |
|
1 |
= 0 |
|
|
|
Z1 |
|
|
|
Z2 |
|
Z3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
. |
(3.2.12) |
|||
|
|
−U2 |
|
|
E2 −U2 |
|
|
|
|
||||||
U1 |
+ |
|
− I00 = 0 |
|
|||||||||||
|
|
Z2 |
|
|
|
Z4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Первое уравнение записано для верхнего левого узла, второе – для верхнего правого узла. Для упрощения написания уравнений все токи, записываемые по закону Ома, считались втекающими (знак тока автоматически приводиться в соответствие со знаками потенциалов законом Ома). Во втором слагаемом первого уравнения для наглядности явно записано нулевое значение потенциала нижнего узла. Отметим, что при таком написании системы не потребовалось преобразований источников напряжения в источники тока. Проведя математические преобразования, легко убедиться, что данная система сводится к каноническому виду (3.2.7).
При записи систем (3.2.3), (3.2.5) полагалось, что все источники напряжения в схеме имеют внутреннее сопротивление, а если они идеальны, то последовательно с ними стоят сопротивления, которые можно принять за их внутренние сопротивления. В случае, когда ветви цепи образуют идеальные источники напряжения – источники ЭДС, расчет цепи методом узловых потенциалов требует специального подхода. Трудность прямолинейного использования закона Ома (проводимость этой ветви бесконечна) для записи тока в таких источниках ЭДС легко обходится. Для этого поступают следующим образом. В схемах, содержащих одну такую ветвь, за базисный узел берут один из узлов этой ветви. Тогда узловое напряжение другого узла равно ЭДС источника и для
47
него не требуется записи уравнения, в которое входит слагаемое с бесконечной проводимостью. Для определения неизвестных узловых потенциалов (их количество равно q - 2) достаточно записать q - 2 уравнения для оставшихся узлов. В схемах с несколькими ветвями, состоящими из идеальных источников ЭДС, явно вводят неизвестные токи в источниках ЭДС (I0i). Естественно, что эти токи не могут быть бесконечными, так как они задаются суммой токов в ветвях, присоединенных к одному из узлов источника. Такой подход позволяет формально записать систему уравнений, основанных на законе токов Кирхгофа. Общего увеличения количества неизвестных не происходит, так как разница узловых напряжений на концах каждой такой ветви равна
ЭДС (Еn) источника этой ветви (Ui +Uk = En ). Решение полученной
системы сильно упрощается, если заметить, что введенные токи входят с разными знаками в уравнения для узлов, к которым присоединен источник. Поэтому попарное сложение этих уравнений устраняет введенные токи и понижает ранг системы на количество ветвей, состоящих из одних идеальных источников напряжения.
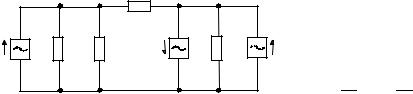
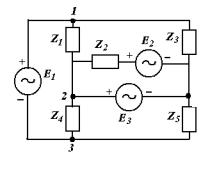
Пример 3.2.2. Найдем токи в ветвях схемы, приведенной на рис. 3.2.4.
Параметры |
схемы: E1 = j В, |
E2 = 1 В, E3 = -j В, Z1 = -j Ом, Z2 = 1 Ом, |
|||
|
|
|
Z3 = 1 Ом, Z4 = 1 Ом, Z5 = j Ом. В |
||
|
|
|
этой схеме две ветви состоят из |
||
|
|
|
источников ЭДС (E1 и E3) и |
||
|
|
|
связывают разные узлы. Поэтому, |
||
|
|
|
если один узел с любой из этих |
||
|
|
|
ветвей |
взять за базисный, то в |
|
|
|
4 |
другой |
ветви ток |
должен быть |
|
|
|
новой переменной. Пусть базисным |
||
|
|
|
узлом будет крайний правый. На |
||
|
|
|
рис. 3.2.4 он обозначен цифрой 4. |
||
|
Рис. 3.2.4 |
|
Тогда ток в ветви с E1 обозначим I01. |
||
|
|
Будем считать, что его направление |
|||
совпадает с |
направлением |
ЭДС. |
Заземлим |
базисный |
узел (положим |
потенциал равным нулю). Тогда потенциал узла 2 определяется идеальным источником напряжения Eз: U2 = E3 = − j В. Если положить потенциал
узла 3 равным Uз = ϕ , то потенциал узла 2 будет больше потенциала узла 2 на величину ЭДС источника E1: U1 = Uз + E1 = ϕ + j. Таким образом, общее количество неизвестных осталась равным q – 1 = 3. Составим систему уравнений токов Кирхгофа, используя узлы 1 и 3. При этом не будем использовать канонический вид записи, а будем явно выражать токи в ветвях через закон Ома. Тогда, полагая для простоты, что токи втекают в узлы, получаем
48
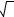
U |
2 |
−U |
1 |
+ |
0 −U |
1 |
+ I01 |
= 0, |
|
Z1 |
Z3 |
||||||
|
|
|
|
|
|
|
||
|
|
−U3 |
|
0 −U3 |
|
|
||
U2 |
+ |
− I01 |
= 0. |
|||||
|
|
Z4 |
|
Z5 |
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
(3.2.13)
Эту систему можно преобразовать к каноническому виду, запись которой можно было провести непосредственно, если источник ЭДС E1 мысленно заменить источником тока I01:
(Y |
+Y )U |
|
−Y U |
|
= I |
|
, |
. |
(3.2.14) |
1 |
3 |
1 |
1 |
2 |
|
01 |
|
||
(Y4 +Y5 )U3 −Y4U2 = −I01 . |
|
|
|||||||
Системы (3.2.13) и (3.2.14) не имеют вида полной системы относительно всех узлов, так как значение потенциала узла 2 уже известно. Отличительная особенность этих систем заключается в том, что, несмотря на наличие двух уравнений при трех неизвестных, они допускают однозначное определение напряжений U1 и U3. Это связано с характером вхождения неизвестного тока в источнике E1 в уравнения: в одно уравнение он входит со знаком “–”, а в другое – со знаком “+”. При определенном навыке расчетов схем этим можно пользоваться при составлении систем уравнений на узловые потенциалы. Сформулируем правило: для узлов связанных ветвью из источника ЭДС вместо двух уравнений, записывается одно – сумма токов втекающих в эту ветвь
равна сумме токов из нее вытекающих. В данном случае I4 + I5 = I1 + I3 .
Подставляя в системы (3.2.13) или (3.2.14) численные значения, используя знание потенциала в узле 2 и связь между потенциалами в узлах 1 и 3, получаем уравнение
( j +1)(ϕ + j) − j(− j) = (1− j)ϕ −1(− j) . |
(3.2.15) |
Откуда U3 =ϕ =1− j , U1 =1. Зная все потенциалы, по закону Ома находятся все токи в ветвях. Например, ток в Z3:
I =U3 −0 |
=1− j =−1− j = 2ej |
5 |
π . |
|
|
4 |
(3.2.16) |
||||
3 |
Z3 |
j |
|
||
|
|
||||
Направление тока I3 выбрано от узла 3 к узлу 4.
3.3. Метод суперпозиции (наложения)
Физический смысл метода наложения основан на линейности пассивных элементов и внутренних сопротивлений активных элементов. Метод реализуется как для токов, так и для узловых потенциалов. В первом случае токи в ветвях или контурах рассчитывают как
49

алгебраическую сумму токов, возникающих от каждого источника в отдельности. Во втором случае узловые напряжения любого узла находят алгебраическим сложением узловых напряжений, созданных на этом узле каждым источником.
Реализацию метода осуществляют последовательным расчетом токов или узловых напряжений с одним источником или с целой группой источников, имеющихся в цепи. Окончательный расчет завершают алгебраическим сложением полученных решений. Исключаемые в расчетах источники заменяют их внутренним сопротивлением.
Пример 3.3.1. Методом суперпозиции найдем токи в ветвях цепи, приведенной на рис. 3.1.3. При этом ограничимся расчетом тока в сопротивлении Z3. остальные токи найдите самостоятельно. Ток в Z3 запишем как сумму токов возникающих вследствие действия каждого
источника |
|
|
|
|
|
|
|
|
IZ |
= IE |
+ IE |
2 |
+ II |
. |
|
(3.3.1) |
|
|
3 |
1 |
|
|
00 |
|
|
|
Расчет |
начнем |
с |
определения тока |
IE |
, вызываемого источником |
|||
|
|
|
|
|
|
|
1 |
|
напряжения Е1. Для этого, во-первых, отсоединим источник тока I00 или просто разорвем эту ветвь, так как внутреннее сопротивление идеального источника тока бесконечно. Во-вторых, удалим из цепи идеальный источник E2, места его присоединения соединим (для краткости будем
Z1 |
IE1 |
|
Z3 |
IE2 |
|
Z3 |
Z1 |
Z2 |
Z4 |
E1 |
Z2 |
|||
|
Z4 |
|
E2 |
|
Рис. 3.3.1 |
|
Рис. 3.3.2 |
|
|
говорить, что источник ЭДС замыкаем), так как его внутреннее сопротивление равно нулю. Получившаяся схема приведена на рис. 3.3.1. Эффективное сопротивление, присоединенное к источнику E1, равно
Z |
ef 1 |
= Z |
+ |
(Z3 + Z4 )Z2 |
. |
(3.3.2) |
|
|
|||||||
|
1 |
Z2 |
+ Z3 + Z4 |
|
|||
|
|
|
|
|
|||
Ток через сопротивление Z1 равен
50
