
Мищенко А. М. Лекции по электротехнике
.pdf
§2. Электрические цепи синусоидального тока
2.1.Общие положения
В линейных электрических цепях синусоидальные токи и напряжения при всех преобразованиях остаются синусоидальными. Именно поэтому этот частный случай особенно важен как в теории электрических цепей, так и на практике. Теория синусоидальных токов лежит в основе метода спектрального анализа, позволяющего исследовать цепи с произвольной формой сигнала. На практике силовая аппаратура и бытовая техника для питания в основном используют синусоидальное напряжение.
При рассмотрении цепей переменного тока предполагается выполнение условий квазистационарности, состоящих в том, что время τ распространения элекромагнитной волны по всей цепи много меньше периода наивысшей гармоники тока T. Для радиотехнических цепей, длина которых не более метра, величина τ меньше 0,3 10-8 с. и токи можно считать квазистационарными вплоть до частот f = 1/T порядка 100 МГц. При этих частотах электрические поля в цепи можно считать статическими и для расчетов мгновенных значений тока и напряжения использовать закон Ома.
В рассматриваемых цепях напряжения и токи источников являются синусоидальными функциями времени, которые можно записать в виде
ek (t) = Ek sin(ωkt +ψk ) ; |
(2.1.1) |
in (t) = In sin(ωnt +ψn ) , |
(2.1.2) |
где Ek и In – амплитудные значения ЭДС и тока |
источников k и n; |
ωk ,n = 2πfk ,n и ψk ,n - соответственно частоты |
и начальные фазы |
источников. |
|
Используя запись синуса в комплексной форме, ЭДС и ток этих источников запишем в виде (в электротехнике мнимая единица обозначается буквой j)
e (t) = Im[E |
k |
e j(ωk t +ψ k ) ] = Im(E |
k |
e jψ k e jωk t ) = Im[E& |
e jωk t ] ; |
(2.1.3) |
||||
k |
|
|
|
|
|
k |
|
|
||
i (t) = Im[I |
n |
e j(ωnt +ψ n ) ] = Im[I |
n |
e jψ n e jωnt ] = Im[I& |
e jωnt ] , |
(2.1.4) |
||||
n |
|
|
|
|
n |
|
|
|
||
где E&k = Ek e jψ k и I&n = Ine jψ n
ЭДС и тока источников k и n. являются модулями
– комплексные амплитудные значения
Действительные амплитуды ЭДС и тока комплексных амплитуд
Ek = E&k = 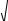 E&k E&k* =
E&k E&k* = 
 Ek e jψ k Ek e− jψ k и аналогично In =
Ek e jψ k Ek e− jψ k и аналогично In = 
 I&n I&n* = I&n ,
I&n I&n* = I&n ,
где знак “*”означает комплексное сопряжение.
21

В последующих параграфах, для упрощения записи, точка над комплексной амплитудой будет опускаться там, где ее нельзя спутать с действительной амплитудой.
На практике измерительные приборы обычно регистрируют среднеквадратичные (действующие) значения напряжений и токов за период их изменений. Например, действующее напряжение
UD = |
1 |
T u2dt = Um |
1 |
T |
(1 |
−cos 2ωt)dt = Um |
, |
(2.1.5) |
|
|
T |
∫ |
2 |
T |
∫ |
|
2 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
где Um – амплитудное значение напряжения. В дальнейшем заглавные буквы с индексом m будут соответствовать амплитудным значениям величин.
Мгновенная мощность p(t), равная произведению тока на напряжение: p(t) =Um sin(ωt +ψ )Im sin(ωt +ψ1) =
|
|
|
|
|
(2.1.6) |
|
= |
1 Um Im[cos(ψ −ψ1) −cos(2ωt +ψ +ψ1 )]. |
|||
|
|
2 |
|
|
|
Средняя мощность за период |
|||||
P = |
1 |
T |
pdt = Um |
Im |
cos(ψ −ψ1) = |
|
T |
∫ |
2 |
2 |
(2.1.7) |
|
|
0 |
|
|
|
= 12 Um Im cos(ψ −ψ1) =UD ID cosϕ,
где ϕ – разность фаз между напряжением и током. Мощности p(t) и P
представляют собой мгновенное значение мощности и мощность, среднюю за период, как в отдельном элементе цепи, так и в участке (ветви) цепи в зависимости от того, соответствуют ток и напряжение отдельному элементу или участку цепи. Для удобства записи мощности величины ЭДС и токи источников в цепях синусоидального тока выражают через действующие значения.
2.2. Законы Ома и Кирхгофа в комплексной форме. Принцип суперпозиции
Расчеты электрических цепей эффективно проводят с применением функций комплексных переменных. Напряжения и токи выражаются через комплексные амплитуды аналогично из выражений (2.1.1), (2.1.2):
u(t) =Um sin(ωt +ψ ) = Im[Ume |
jψ |
e |
jωt |
& |
jωt |
] ; |
(2.2.1) |
|
|
] = Im[Ue |
|
||||
i(t) = Im sin(ωt +ψ1) = Im[Ime jψ1 e jωt ] = Im[I&e jωt ] , |
|
(2.2.2) |
|||||
22

где U& = Ume jψ , I& = Ime jψ1 – комплексные амплитуды, а Um, Im –
действительные амплитуды напряжения и тока (модули комплексных амплитуд), ψ и ψ1 – фазы напряжения и тока (аргументы комплексных амплитуд). Переход от комплексных значений тока и напряжения к реальным значениям осуществляется взятием мнимой части.
Запишем закон Ома для резистора (1.1.1) через комплексные функции:
uR (t) = Im[U&Re jωt ] = R Im[I&e jωt ] = Im[R I&e jωt ] . |
(2.2.3) |
Откуда получаем для резистора закон Ома в комплексной форме |
|
U&R = RI&. |
(2.2.4) |
Отметим, что ток в резисторе и напряжение на нем имеют одну и ту же фазу. Говорят, что они находятся в фазе. Действительные амплитуды
напряжения и тока связаны выражением UR = U&R = RI& = R I& = RI .
Отметим, что оно справедливо и для действующих значений тока и напряжения.
Для индуктивности из выражений (2.2.1), (2.2.2) и закона Ома (1.1.4) получаем
uL (t) = Im[U&Le jωt ] = L dtd {Im[I&e jωt ]}= Im[L dtd {I&e jωt }] = Im[jωLI&e jωt ]. (2.2.5)
При записи выражения (2.2.5) воспользовались возможностью перестановки операций взятия мнимой части и дифференцирования.
Действительно |
d |
{Im[I&e jωt ]} = |
d |
{I |
m |
sin(ωt +ψ)}= I ω cos(ωt +ψ) . С |
||||||
|
|
|||||||||||
|
|
|
dt |
|
dt |
|
m |
|
||||
|
|
|
|
|
|
|
|
|||||
другой |
|
|
|
|
|
|
стороны |
|||||
|
d |
{I&e jωt }] = Im[ jωI&e jωt ] = Im[e j |
π |
|
π ) = |
|||||||
Im[ |
2ωI&e jωt ] = ωIm sin(ωt +ψ + |
|||||||||||
|
||||||||||||
|
dt |
|
|
|
|
|
|
2 |
||||
= ωIm cos(ωt +ψ) , |
где использовано представление мнимой единицы в |
|||||||||||
|
|
π |
|
|
|
|
|
|
|
|||
виде e j 2 . Таким |
образом, согласно выражению (2.2.5), имеем для |
|||||||||||
индуктивности закон Ома в комплексной форме имеет вид |
|
|||||||||||
U&L = jωLI&. |
|
|
|
|
|
|
(2.2.6) |
|||||
Видно, что фаза напряжения на π/2 больше фазы тока. Говорят, что напряжение на индуктивности опережает ток по фазе на π/2. Амплитуды напряжения и тока или их действующие значения на индуктивности
связаны формулой UL = ωLI . По аналогии с резистором сопротивление индуктивности представляют комплексным сопротивлением
23
ZL = jωL . |
(2.2.7) |
Это сопротивление является чисто мнимым и линейно зависит от частоты.
Для случая емкости аналогично с использованием закона Ома (1.1.7) получаем
|
& |
|
|
jωt |
|
1 |
|
& jωt |
|
1 |
|
& |
jωt |
|
1 & |
|
u (t) = Im[U |
|
e |
|
] = |
|
|
Im[Ie |
]dt = Im[ |
|
|
Ie |
|
dt] = Im[ |
|
I]. (2.2.8) |
|
C |
|
C ∫ |
C ∫ |
|
|
|||||||||||
C |
|
|
|
|
|
|
|
|
|
jωC |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UC = |
1 |
|
I . |
|
|
|
|
|
|
|
|
|
|
(2.2.9) |
||
jωC |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При записи выражения (2.2.8) воспользовались справедливостью перестановки операций взятия мнимой части и интегрирования. Покажите самостоятельно справедливость такой перестановки. Видно, что для емкости фаза напряжения на π/2 меньше фазы тока. Говорят, что напряжение на индуктивности отстает от тока по фазе на π/2. Амплитуды напряжения и тока или их действующие значения связаны формулой
UL = I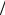 ωC . Тогда сопротивление емкости
ωC . Тогда сопротивление емкости
ZC = − j |
1 |
. |
(2.2.10) |
|
|||
|
ωC |
|
|
Это сопротивление так же является чисто мнимым, но в отличие от сопротивления индуктивности имеет обратно пропорциональную зависимость от частоты.
Пример 2.2.1. Последовательное и параллельное соединение пассивных элементов R, L и C.
При последовательном соединении элементов по ним протекает один и тот же ток, а общее падение напряжения равно сумме напряжений на
каждом элементе, т. е. u(t) = uR (t) +uL (t) +uC (t) . Поэтому, используя выражения (2.2.1), (2.2.3), (2.2.5) и (2.2.8), получаем
& |
& & & |
1 |
& |
& |
|
U |
=UR +UL +UC = (R + jωL + |
jωC |
)I |
= ZI , |
(2.2.11) |
|
|
|
|
|
где введено общее сопротивление цепи Z = ZR + ZL + ZC .
При параллельном соединении элементов обеспечивается равенство напряжений на каждом элементе, тогда как общий ток является суммой токов в каждом из них. Тогда, переходя к комплексным амплитудам и используя законы Ома для элементов R, L и C, получаем
I& = I&R + I&L + I&C = ( |
1 |
+ |
1 |
+ jωC)U& =YU& , |
(2.2.12) |
|
R |
jωL |
|||||
|
|
|
|
24

где введена общая проводимость цепи Y =1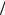 R +1
R +1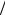 ZL +1
ZL +1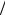 ZC =
ZC =
=YR +YL +YC .
Вобщем случае для произвольного комплексного сопротивления Z запись закона Ома в комплексной форме совпадает по виду с записью закона Ома для постоянного тока:
U& = Z I&. |
(2.2.13) |
При расчетах схем в зависимости от ситуации используется различная запись комплексного сопротивления и проводимости
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z = R + jX = |
|
Z |
|
e jψ = R2 + X 2 (cosψ + j sinψ) ; |
|
(2.2.14) |
|||||||||||||||||
|
|
|
|||||||||||||||||||||
Y = |
1 |
|
|
= g + jy |
= |
R − jX |
= |
R |
+ j(− |
X |
|
) ; |
(2.2.15 а) |
||||||||||
|
|
R2 + X 2 |
R2 + X 2 |
R2 + |
X 2 |
||||||||||||||||||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Y = |
1 |
= |
1 |
|
|
(cosψ + j sin(−ψ )) , |
|
|
|
|
(2.2.15 б) |
||||||||||||
|
Z |
|
e jψ |
|
Z |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где ψ – аргумент комплексного сопротивления; R – вещественная часть комплексного сопротивления, ее называют активным сопротивлением; X – мнимая часть комплексного сопротивления, ее называют реактивным сопротивлением; аналогично, g – активная проводимость; y – реактивная проводимость. Выпишем формулы для нахождения аргумента
tgψ = |
X |
; |
|
(2.2.16) |
||
R |
|
|||||
|
|
|
|
|||
cosψ = |
R |
; |
(2.2.17) |
|||
R2 + X 2 |
||||||
|
|
|
|
|
||
sinψ = |
|
X |
. |
(2.2.18) |
||
|
R2 + X 2 |
|||||
|
|
|
|
|
||
Законы Кирхгофа в комплексной форме записываются простыми линейными уравнениями. Так закон токов Кирхгофа (1.3.1) для узла цепи есть
∑I&n = 0 , |
(2.2.19) |
n |
|
где суммирование ведется по всем ветвям, образующим узел. Закон напряжений Кирхгофа (1.3.2) преобразуется к виду
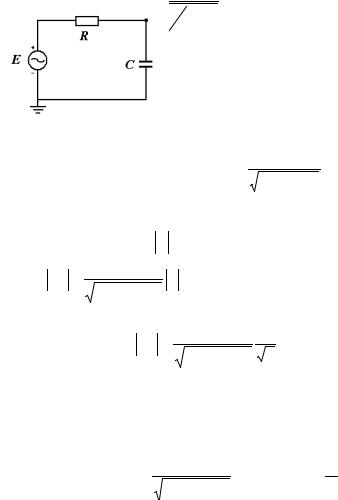
∑E&n = ∑U&n , |
(2.2.20) |
n n |
|
25
где суммирование ведется по всем источникам ЭДС и пассивным элементам, входящим в выделенный замкнутый контур.
Пример 2.2.2. Найдем напряжения на емкости и сопротивлении в схеме, приведенной на рис. 2.2.1. Ток в цепи из закона напряжений Кирхгофа
I& = |
E& |
= |
|
E& |
|
|
e |
− jψ |
, |
|
|
|
|
|
|
(2.2.21) |
|
R + 1 jωC |
R2 + |
1 |
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(ωC) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
ψ = arctg(− |
1 |
|
) – |
аргумент |
||||||
|
|
|
|
|
|
RωC |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
комплексного |
сопротивления |
цепи. |
|||||||||||
|
|
|
|
Величина ψ определяет разность фаз |
|||||||||||||
|
|
|
|
между током и ЭДС. Тогда комплексное |
|||||||||||||
|
|
|
|
напряжение на емкости |
|
|
|
|
|
||||||||
|
|
|
|
U& |
=Z I& |
= |
|
1 |
|
E&e |
− j( |
π +ψ) |
. (2.2.22) |
||||
|
|
|
|
|
|
|
|
2 |
|||||||||
|
Рис. 2.2.1 |
|
C |
|
|
C |
|
|
(RωC)2 +1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Напряжение, измеряемое вольтметром (V), будет равно модулю этого напряжения, если полагать, что модуль ЭДС источника соответствует
действующему значению ( E& = ED ) т. е.
V = U&C = |
1 |
E& . |
(2.2.23) |
|
(RωC)2 +1 |
||||
|
|
|
Если же модуль ЭДС источника соответствует амплитудному значению
( |
|
E& |
|
= Em ), то V = U&C = |
1 |
Em |
. Обычно для цепей |
|
|
||||||
|
|
|
|
|
(RωC)2 +1 |
2 |
|
синусоидального тока в целях для удобства значения ЭДС и токи источников выражают через действующие величины, опуская нижний индекс. Мгновенное напряжение на емкости можно измерить осциллографом. Оно получается из комплексной амплитуды умножением
на e jωt и взятием мнимой части:
& |
jωt |
) = |
1 |
Em sin(ωt −ψ − |
π |
) . |
(2.2.24) |
uC (t) = Im(UC e |
|
(RωC)2 +1 |
2 |
||||
|
|
|
|
|
|
Аналогично находится напряжение на резисторе:
26

& |
jωt |
) = |
RωC |
Em sin(ωt −ψ) . |
(2.2.25) |
uR (t) = Im(URe |
|
(RωC)2 +1 |
|||
|
|
|
|
|
Отметим важную особенность данной цепи. При малых частотах (ω <<1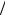 RC ) напряжение на емкости примерно равно ЭДС источника, а
RC ) напряжение на емкости примерно равно ЭДС источника, а
при больших (ω >>1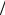 RC ) стремится к нулю. Наоборот напряжение на резисторе с уменьшением частоты (ω <<1
RC ) стремится к нулю. Наоборот напряжение на резисторе с уменьшением частоты (ω <<1 RC ) стремится к нулю, а с увеличением частоты (ω >>1
RC ) стремится к нулю, а с увеличением частоты (ω >>1 RC ) – к ЭДС источника. Это является
RC ) – к ЭДС источника. Это является
прямым следствием частотной зависимости сопротивления емкости. При малых частотах сопротивление емкости значительно превосходит
сопротивление резистора (при ω = 0 сопротивление емкости ZC = ∞, что
соответствует разрыву цепи) и, как в случае простого делителя напряжения на резисторах, основное падение напряжения происходит на емкости. При больших частотах сопротивление емкости становиться меньше сопротивления резистора и основное падение напряжения происходит на резисторе.
Разность фаз между током и ЭДС стремится к нулю в области больших частот и стремится к – π/2 при малых частотах. Поэтому напряжение на сопротивлении полностью повторяет временную зависимость ЭДС при больших частотах, тогда как напряжение на емкости
– при малых частотах. Этим свойством RC цепочек пользуются для фильтрации сигнала. При устранении низкочастотных помех сигнал снимают с резистора, а при устранении высокочастотных помех сигнал снимают с емкости. Подробнее это рассмотрено в § 4.
При записи уравнения (2.2.20) предполагается, что все источники ЭДС работают на одной частоте. При наличии в контуре источников с разной частотой в силу линейности цепи пользуются принципом суперпозиции.
Согласно этому принципу каждый источник не зависимо от остальных создает в элементах цепи свой ток и свое напряжение на них так, что реальный ток в элементе или напряжение на нем является алгебраической суммой (суперпозицией) этих токов, а реальное напряжение на элементе является алгебраической суммой (суперпозицией) этих напряжений.
Пример 2.2.3. |
Рассчитаем токи в контуре, состоящем из |
|||
последовательно |
соединенных |
двух |
источников |
ЭДС: |
e1(t) = E1 sin(ω1t +ψ1) , e2 (t) = E2 sin(ω2t +ψ2 ) |
и пассивных элементов |
|||
R, L, C. Уравнение по закону напряжений Кирхгофа в интегродифференциальном виде есть
e (t) +e (t) = Ri(t) + L |
di(t) |
+ |
1 |
i(t)dt . |
(2.2.26) |
|
|
|
|||||
1 |
2 |
dt |
|
C ∫ |
|
|
|
|
|
|
|||
27
Представим ток суммой двух токов: |
i(t) = i1(t) +i2 (t) и будем полагать, |
||||||||||||||||||||||
что введенные токи i1(t) и i2 (t) |
удовлетворяют уравнениям |
|
|
|
|
|
|||||||||||||||||
e (t) = Ri (t) + L |
di1(t) |
|
|
+ |
|
1 |
∫ |
i (t)dt ; |
|
|
|
|
|
(2.2.27) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
1 |
|
|
dt |
|
|
|
C |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
e (t) = Ri (t) |
+ L |
di2 (t) |
|
|
+ |
1 |
∫ |
i (t)dt . |
|
|
|
|
|
(2.2.28) |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
2 |
|
|
dt |
|
|
|
C |
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда суммируя уравнения (2.2.27) и (2.2.28) получаем |
|
|
|
|
|
||||||||||||||||||
e (t) |
+e (t) |
= Ri (t) + L |
di1(t) |
+ |
1 |
i (t)dt + Ri (t) + L |
di2 (t) |
+ |
1 |
i |
(t)dt . |
||||||||||||
|
|
|
|
||||||||||||||||||||
1 |
2 |
1 |
|
|
|
dt |
|
|
|
|
C ∫ |
1 |
2 |
dt |
|
C ∫ |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Это выражение получается и прямой подстановкой суммы токов в уравнение (2.2.26). Таким образом, реальный ток можно представлять суперпозицией токов созданных, каждым источником в отдельности независимо друг от друга. Причем зависимость ЭДС от времени может быть произвольной. В рассматриваемом случае синусоидальных
напряжений токи i1(t) и i2 (t) легко находятся методом комплексных
амплитуд. Для этого уравнения Кирхгофа (2.2.27) и (2.2.28) запишем в комплексной форме:
& |
|
|
|
|
|
|
|
|
|
|
1 |
|
& |
|
& |
|
|
|
|
|
||
E |
= (R + jω L |
+ |
|
jω |
C |
)I = Z(ω )I ; |
|
|
|
(2.2.29) |
||||||||||||
1 |
|
|
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
& |
|
|
& |
|
|
|
||
E2 |
= (R + jω2 L + |
|
|
|
|
|
|
)I2 |
= Z (ω2 )I |
2 , |
|
|
(2.2.30) |
|||||||||
|
jω2C |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где E& |
= E e jψ1 , E& |
|
= E |
2 |
e jψ |
2 . Отсюда |
|
|
|
|
|
|
||||||||||
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i (t) = Im[ |
|
E e jψ1 |
|
e |
jωt |
|
|
|
|
|
E |
|
|
|
sin(ωt +ψ |
|
|
|||||
|
1 |
|
|
|
|
1 |
] = |
|
|
|
1 |
|
|
|
|
−ϕ ) ; (2.2.31) |
||||||
Z(ω ) |
|
e jϕ1 |
|
|
|
|
|
|
|
1 |
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
1 |
1 |
1 |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
+(ω L − |
|
|
)2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
i (t) =Im[ |
E ejψ2 |
|
e |
jω |
t |
|
|
E |
|
sin(ω t +ψ |
|
|
|||
2 |
|
|
|
2 |
|
] = |
|
2 |
|
|
−ϕ ) , (2.2.32) |
||||
Z(ω ) |
|
ejϕ2 |
|
|
|
1 |
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|||
|
|
2 |
|
|
|
|
|
|
|
R2 +(ω L − |
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
ω C |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
где |
tg(ϕ ) = ω1L +1 |
ω1C , |
tg(ϕ |
) = ω2 L +1 ω2C – |
выражения для |
||||||||||
|
1 |
|
|
R |
|
|
|
2 |
|
|
R |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
определения аргументов комплексного сопротивления цепи на двух частотах.
28

|
Пример 2.2.4. Рассмотрим широко используемую в электронике цепь |
||||||||||
|
из |
последовательно |
соединенного |
|
|
|
|||||
|
резистора и конденсатора. Пусть эта цепь |
|
|
|
|||||||
|
подключена к источнику напряжения, |
|
|
|
|||||||
|
имеющему |
постоянную |
составляющую |
и |
|
|
|
||||
|
переменную |
– |
синусоидальную. На |
|
|
|
|||||
|
рис. 2.2.2. изображена такая цепь с |
|
|
|
|||||||
Рис. 2.2.2 |
синусоидальным источником напряжения с |
|
|
|
|||||||
комплексной амплитудой E1 и |
с |
|
|
|
|||||||
|
|
|
|
||||||||
|
источником |
постоянного |
напряжения |
с |
|
|
|
||||
|
ЭДС равной E2. Будем полагать, что |
|
|
|
|||||||
|
включение источников произошло достаточно давно, и цепь пришла в |
||||||||||
|
квазиравновесное (стационарное) состояние. Линейность электрической |
||||||||||
|
цепи (R и C не зависят от протекающего тока) позволяет воспользоваться |
||||||||||
|
принципом |
суперпозиции i(t) = i1(t) +i2 (t) , где |
токи |
i1(t) и |
i2 (t) |
||||||
|
определяются соответственно источниками ЭДС E1 и E2. Для нахождения |
||||||||||
|
тока i1(t) воспользуемся формулой (2.2.31). Тогда имеем |
|
|
||||||||
|
i1 |
(t) = |
E1ωC |
|
sin(ωt +ψ) , |
|
|
|
(2.2.33) |
||
|
|
|
|
|
|
|
|||||
|
|
(RωC)2 +1 |
|
|
|
|
|
||||
|
где |
ψ = arctg( |
1 |
|
) . |
Для нахождения тока |
i (t) |
можно |
также |
||
|
|
|
|||||||||
|
|
|
|
RωC |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
формально воспользоваться выражением (2.2.32), сделав в нем предельный переход ω2 → 0 . Такой формализм приводит к естественному значению
i2 (t) = 0 , которое означает, что постоянный ток не проходит через емкость.
Таким образом, напряжение на резисторе определяется только синусоидальным током, вызванным ЭДС E1 и при заданной частоте
выбором величины конденсатора ( C >> 1ωR ) может доведено
практически до величины пользуются в электронике постоянной составляющей.
E1. Этим свойством RC цепочек широко для отделения переменного сигнала от
Напряжение на емкости кроме переменной составляющей
u1(t) = |
E1 |
sin(ωt +ψ − |
π |
) =− |
E1 |
cos(ωt +ψ) (2.2.34) |
|
(RωC)2 +1 |
2 |
(RωC)2 +1 |
|||||
|
|
|
|
имеет постоянное напряжение u2 = E2 . Это стационарное напряжение на емкости возникает при подключении цепи к источнику напряжения, и оно
29
препятствует протеканию постоянного тока, обеспечивая нулевое напряжение на резисторе. Подробно о поведении цепей при переходе от одного стационарного состояния к другому рассмотрено в § 5.
Полная система уравнений для расчета токов в ветвях для случая цепей синусоидальных источников получается также как и в случае цепей постоянного тока. Поэтому ее легко записать на основе системы уравнений (1.5.1) путем замены токов и ЭДС на соответствующие комплексные амплитуды, а сопротивления Rks на комплексные сопротивления пассивных элементов Zks
|
r |
|
|
m (1, q −1), |
|
|
∑I&km = 0 , |
|
|||
|
|
|
|
. |
(2.2.35) |
S k |
S |
|
|||
∑E |
E&ks = ∑Z |
Zks I&ks , |
s (1, p −q +1). |
|
|
|
k |
k |
|
|
|
В этой системе уравнений также предполагается, что источники ЭДС работают на одной и той же частоте. Поэтому при работе в схеме источники с разной частотой, необходимо воспользоваться принципом суперпозиции. Тогда расчет проводится раздельно для каждой группы источников с одинаковой частотой. Остальные источники из электрической цепи удаляются. Удаление источника производят замыканием идеального источника напряжения, тогда как элементы схемы, изображающие внутреннее сопротивление источника, остаются включенными в схему. Реальные токи находят суперпозицией рассчитанных токов.
При наличии в цепи источников тока, с ними поступают, так же как указано в § 1 для цепей постоянного тока. Дополнительные способы расчета цепей с источниками тока рассмотрены в § 3.
2.3. Комплексная мощность
Использование комплексной формы записи токов и напряжений позволяет проводить усреднение по времени с помощью простой операции: взятия модуля. Например, действующее значение напряжения
получают как UD = |
U&eiωtU& e−jωt |
= |
U&me jψU&me−iψ |
|
Um2 |
= |
1 |
Um |
|||
2 |
|
|
2 |
= |
|
2 |
|
||||
|
|
|
|
|
|
|
2 |
||||
или с использованием закона Ома: |
UD = |
1 |
& |
& |
= |
1 |
|
& |
, где |
||
2 |
ZIZ I |
2 |
Z Im |
||||||||
|
|
|
|
|
|
|
|
|
|
||
Z – модуль комплексного сопротивления. Двойка в знаменателе нужна
лишь при определении напряжений (или токов) через амплитудные значения. Это позволяет определить полную мощность S для участка цепи
30
