
Мищенко А. М. Лекции по электротехнике
.pdfчерез произведение комплексного напряжения и комплексносопряженного тока:
S = |
1 |
U I = |
1 |
Ume jψ Ime− jψ1 = |
1 |
Um Ime j(ψ −ψ1 ) = |
|
||
2 |
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|||
= |
1 Um Im cos(ψ −ψ1) + j |
1 Um Im sin(ψ −ψ1) = |
(2.3.1) |
||||||
|
2 |
|
|
|
|
2 |
|
|
|
=U D ID cos(ψ −ψ1 ) + jU D ID sin(ψ −ψ1 ) .
Действительная часть (P) полной мощности (S) является активной мощностью, рассеиваемой в данном участке цепи, а мнимая (Q) – реактивной мощностью. Последняя строчка записана с использованием вместо амплитудных значений напряжения и тока их действующие значения. Эта простая запись получила наибольшее распространение в технике.
Выпишем ряд часто используемых выражений:
Re(S) = P = |
1 Um Im cos(ψ −ψ1) =UD ID cos(ψ −ψ |
1) ; |
(2.3.2) |
|
2 |
|
|
Im(S) = Q = |
1 Um Im sin(ψ −ψ1) =UD ID sin(ψ −ψ1) ; |
(2.3.3) |
|
|
2 |
|
|
S = |
1 U& |
|
I& = |
|
1 Z I& I& |
= 1 Z Im2 |
= Z ID2 ; |
|
(2.3.4 а) |
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S = |
1 U& |
|
I& = |
|
|
1 U& |
|
U& Y = |
|
1 Um2 |
|
Y =U D2 Y ; |
(2.3.4 б) |
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Z = |
2S |
|
= |
2P |
|
+ j |
2Q |
= |
|
S |
= |
|
P |
+ j |
Q |
|
; |
|
|
(2.3.5) |
|||||||||||||
Im2 |
|
|
|
|
|
|
|
|
ID2 |
ID2 |
|
|
|||||||||||||||||||||
|
|
|
|
Im2 |
|
|
|
|
Im2 |
|
|
ID2 |
|
|
|
|
|
|
|
|
|
||||||||||||
Y = |
2S |
|
= |
|
2P |
|
− j |
2Q |
= |
|
S |
|
= |
|
P |
|
− j |
|
Q |
|
. |
(2.3.6) |
|||||||||||
Um2 |
|
Um2 |
|
Um2 |
UD2 |
UD2 |
|
UD2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Полная мощность, развиваемая идеальным источником напряжения:
SE = E&I&* . |
(2.3.7) |
Полная мощность, развиваемая идеальным источником тока:
S |
|
& & |
* |
. |
(2.3.8) |
I |
= I U |
|
|||
|
0 |
|
|
|
Направление тока в источнике напряжения соответствует переносу положительного заряда сторонними силами, т. е. перемещению от минуса к плюсу. Другими словами, это то направления тока, которое возникает в нагрузке при подсоединении ее к источнику. Напряжение на источнике
31
тока определяется нагрузкой. Оно отсчитывается от узла, из которого ток втекает в источник тока. При Re(S) > 0 источник поставляет во внешнюю
цепь энергию, а при Re(S) < 0 потребляет. В последнем случае источник
уже не генератор, вырабатывающий электричество, а мотор, вращаемый внешним генератором. Для реальных источников необходимо учитывать потери на внутренних сопротивлениях. Поэтому в источнике тока даже при отсоединенной нагрузке идет рассеивание энергии. Для определения полной мощности поставляемой (развиваемой источником) во внешнюю цепь необходимо пользоваться общим выражением (3.1), где ток и напряжение соответствуют значениям на клеммах источника.
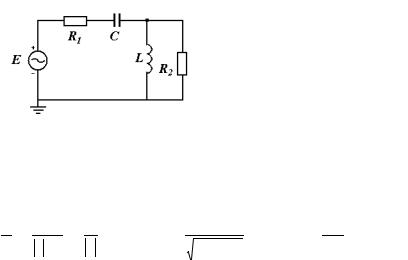
Пример 2.3.1. Найдем мощность, поставляемую источником, в схеме представленной на рис. 2.3.1 и мощность, выделяемую на сопротивлении R2.
Сопротивление нагрузки
|
Z = R |
+ Z |
C |
+ |
ZL R2 |
= R − j |
1 |
|
+ j |
ωLR2 (R2 − jωL) |
= |
|||||||||||||||
|
|
|
|
ωC |
||||||||||||||||||||||
|
|
1 |
|
|
|
|
Z |
L |
+ R |
1 |
|
|
|
|
|
(ωL)2 + R2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
(2.3.9) |
||||
|
|
|
|
|
1 |
|
|
|
ωLR2 |
|
|
|
(ωL)2 R |
|
|
|
||||||||||
|
= R − j |
+ j |
|
|
|
|
= R |
+ jX , |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
+ |
|
|
|
|
|
2 |
|
|
|||||||||
|
ωC |
(ωL)2 + R2 |
(ωL)2 + R2 |
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|
'ЭФ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
RЭФ = R1 + |
|
(ωL)2 R |
|
|
|
|
|
|
|
|
|
||||||||||
где |
|
|
|
|
|
|
2 |
|
|
– |
|
|
|
|
|
|
|
|||||||||
|
|
|
(ωL)2 + R2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
эффективное |
|
|
|
|
|
|
|
активное |
|
|
|
|
|
|
|
|||||||||||
сопротивление |
|
|
|
|
|
|
нагрузки, |
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
ωLR22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
X = − |
|
+ |
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ωC |
(ωL)2 + R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.3.1 |
|||
эффективное мнимое сопротивление |
|
|
|
|
||||||||||||||||||||||
нагрузки, которое можно рассматривать кок последовательное соединение |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LЭФ = |
|
LR2 |
|
|
|
емкости с эффективной индуктивностью |
|
2 |
|
. |
||||||||||||||||||||||
(ωL)2 + R2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Ток, развиваемый источником, есть |
|
|
|
|
|
|
|
||||||||||||||||||
& |
E& |
& |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
X |
||||
I |
=Z |
=E Zejψ |
=E Z exp(j(ϕ−ψ))=E R2 |
+X2 |
exp(j(ϕ−arctgRЭФ)), (2.3.10) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЭФ |
|
|
|
|
|
|
||
где для общности введена фаза источника (φ). Тогда потребляемая нагрузкой мощность, равная мощности, развиваемой источником, есть (ЭДС источника считаем действующей)
32
* |
&* |
jψ |
|
|
|
2 |
1 |
|
|
|
|
|
||
E |
|
|
|
|
|
|
|
|
||||||
P =Re(E&I& |
) =Re(E& |
Z e |
|
) =Re(E |
RЭФ2 + X 2 exp(jψ))= |
|
|
|||||||
= E 2 |
1 |
cos(ψ ) = E 2 |
|
RЭФ |
|
|
, |
|
|
|
(2.3.11) |
|||
RЭФ2 + X 2 |
|
|
|
|
RЭФ2 + |
X 2 |
|
|
|
|
|
|||
где использовано выражение |
cosψ = |
|
RЭФ |
. Эту |
же |
формулу |
||||||||
|
R2 |
|
+ X 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ЭФ |
|
|
|
|
|
можно получить, используя выражение |
|
для |
напряжения |
на |
нагрузке |
|||||||||
U& = ZI&. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = Re(U&I&) = Re(ZI 2 ) = R |
I 2 |
= R |
|
|
E2 |
. |
|
(2.3.11 а) |
||||||
|
|
|
+ X 2 |
|
||||||||||
|
|
|
|
ЭФ |
|
ЭФ R2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
ЭФ |
|
|
|
|
|
Видно, что рассеиваемая мощность минимальна при частотах, близких к нулю. В пределе постоянной ЭДС ток через нагрузку не течет и потребления энергии нет. Максимальное потребление энергии в единицу времени происходит при частоте, на которой реактивная составляющая сопротивления равна нулю. Эта частота есть
ω = |
|
|
|
R22 |
|
|
=ω |
|
|
1− ρ2 |
|
, где ω |
|
=1 |
|
, ρ = |
|
. |
||
|
|
|
|
0 |
|
R22 |
0 |
LC |
L C |
|||||||||||
|
R2CL − L2 |
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда максимальная потребляемая мощность |
|
|
|
|
|
|
||||||||||||||
|
P = |
|
E2 |
= |
|
|
E2 |
|
|
. |
|
|
|
(2.3.12) |
||||||
|
|
R |
R |
+ ρ |
R |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ЭФ |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Для определения рассеиваемой мощности на сопротивлении R2 необходимо найти протекающий через него ток. Для этого найдем напряжение в верхнем узле (нижний узел заземлен):
& |
|
ZL R2 & |
|
jωLR2 & |
|
jωLR2 |
& |
|
U |
= |
ZL + R2 I |
= |
jωL + R2 I |
= |
(ωL)2 + R2 e jφ |
I . |
(2.3.13) |
|
|
|
|
|
|
2 |
|
|
Тогда, используя выражение (2.3.4б), находим искомую рассеиваемую мощность:
P |
|
U |
2 |
(ωL)2 R |
I 2 = |
(ωL)2 R |
|
E2 |
|
|
|
||
= |
|
= |
2 |
2 |
|
|
|
|
|
. |
(2.3.14) |
||
R |
(ωL)2 + R2 |
(ωL)2 + R2 |
R2 |
|
+ |
X 2 |
|||||||
2 |
|
|
|
|
|
|
|||||||
|
|
2 |
2 |
|
2 |
|
ЭФ |
|
|
|
|
||
Покажем, что полная рассеиваемая мощность есть сумма мощностей рассеиваемыми резисторами. Мощность, выделяемая на сопротивлении R2,
33
уже найдена. Найдем теперь мощность, которая рассеивается на сопротивлении R1:
P |
= R I 2 |
= |
R E2 |
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
. |
|
|
|
|
|
|
(2.3.15) |
|||
R2 |
+ X 2 |
|
|
|
|
|
|
|||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
ЭФ |
|
|
|
|
|
|
|
|
|
|
|
Тогда имеем |
|
|
|
|
|
|
|
|
|
|
|
|||
P = P + P |
= (R |
|
+ |
(ωL)2 R |
)I 2 |
= R I 2 |
= E2 |
|
R |
|
|
|||
|
|
2 |
|
ЭФ |
. |
|||||||||
|
(ωL)2 + R2 |
R2 |
|
|||||||||||
|
1 |
2 |
1 |
|
|
ЭФ |
|
|
+ X 2 |
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
ЭФ |
|
|
|
Таким образом, найти полную мощность, рассевающуюся в нагрузке можно двумя способами: 1) найти потребляемый ток, взять от него модуль и квадрат его умножить на активное сопротивление нагрузки; 2) найти мощности, рассеиваемые на каждом резисторе нагрузки и их просуммировать.
2.4. Векторные диаграммы
При расчетах электрических цепей удобно использовать векторные диаграммы, где на комплексной плоскости комплексному напряжению или току соответствует радиус-вектор. Длина вектора пропорциональна действующему или амплитудному значению, а угол поворота от вещественной оси (оси абсцисс) равен мгновенному значению фазы ωt +ψ . Изменение фазы со временем на векторной диаграмме
соответствует вращению векторов против часовой стрелки. Проекции векторов на мнимую ось соответствуют мгновенным значениям тока или напряжения. Так как вращение векторов происходит с одинаковой угловой частотой ω, то относительное расположение нескольких векторов, соответствующих токам и напряжениям в схеме, сохраняется в любой момент времени. Чаще всего интерес представляют именно относительные фазы напряжений и токов. Поэтому векторную диаграмму строят в системе отсчета, вращающейся с частотой ω .
34
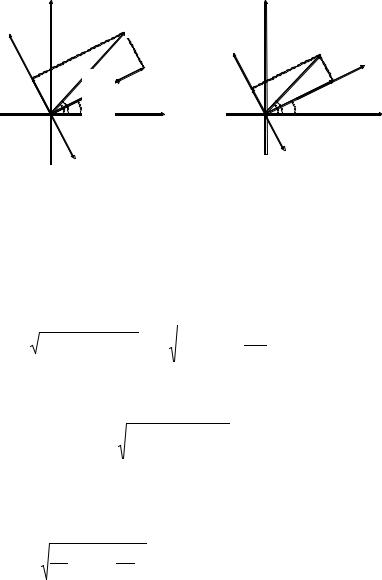
На |
рис. 2.4.1 |
приведена |
такая |
векторная |
диаграмма |
цепи |
с |
|||||||
|
UL |
|
|
U |
|
|
IC |
|
|
|
|
|
|
|
|
|
|
|
|
UR |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UR |
||
UL - UC |
|
Ψ1 |
|
|
|
|
|
|
Ψ1 |
|
|
|||
|
I |
|
|
IC - IL |
|
|
IR |
|
|
|||||
|
|
|
Ψ |
|
|
|
|
Ψ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
UC |
|
|
|
|
|
IL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.4.1 |
|
|
|
|
Рис. 2.4.2 |
|
|
|
|
||||
последовательно соединенными R, L, |
C и заданным током |
I = Ime jψ . |
||||||||||||
Напряжение |
на |
сопротивлении |
находится |
в |
фазе |
с |
током, |
а |
на |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
индуктивности и емкости соответственно опережает или отстает на |
2 . |
|||||||||||||
Поэтому векторы UR и I коллинеарные, а UL, и UC перпендикулярны |
||||||||||||||
вектору I. Полное падение напряжения на цепи находится по правилам |
||||||||||||||
сложения векторов |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Um = UR2 +(UL −UC )2 = Im |
R2 +(ωL − |
1 |
)2 , |
(2.4.1) |
|
|
|
ωC |
|
|
|
а разность фаз между полным напряжением и током определяется углом между векторами U и I
cos(ψ1 |
−ψ) = |
UR |
= |
|
|
R |
|
|
|
. |
(2.4.2) |
|
|
|
|
|
|
|
|||||
|
Um |
|
R |
2 |
+ (ωL − |
1 |
) |
2 |
|
|
|
|
|
|
|
|
ωC |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 2.4.2 приведена векторная диаграмма цепи с параллельным соединением R, L, C. Напряжение на цепи U = Ume jψ . Принцип
построения диаграммы такой же, что и на рис.2.4.1. Полный ток в цепи находится сложением векторов токов IR, IL, IC
I |
|
=U |
1 |
+(ωC − |
1 |
)2 |
, |
(2.4.3) |
|
m |
|
m R2 |
|
ωL |
|
|
|
а разность фаз между напряжением и током равна углу между векторами U и I
35

|
|
|
1 |
|
|
|
|
|
cos(ψ1 |
−ψ) = |
|
R |
|
|
. |
(2.4.4) |
|
|
|
|
|
|||||
|
1 |
+(ωC − |
1 |
)2 |
|
|||
|
|
R2 |
ωL |
|
||||
|
|
|
|
|
|
|
||
Использование векторных диаграмм в ряде случаев оказывается более эффективно, чем применение стандартных методов, основанных на комплексной алгебре.
36
§ 3. Методы расчета электрических цепей
Расчет электрических цепей предполагает нахождение во всех ветвях токов и напряжений по заданным параметрам активных и пассивных элементов. Приведенные методы расчета относятся к синусоидальным и постоянным источникам тока и напряжения. Линейность элементов цепи позволяет обобщить рассматриваемые методы на случай источника с произвольной формой сигнала, представляя его в виде суммы гармоник. Искомые токи и напряжения будут являться суммой токов и напряжений, рассчитанных для гармоник. В случае работы нескольких источников искомые напряжения и токи являются суперпозицией напряжений и токов, рассчитанных для каждого источника в отдельности, когда другие источники удалены из электрической цепи. Удаление источника производят либо замыканием идеального источника напряжения, либо отсоединением идеального источника тока. Элементы схемы, изображающие внутреннее сопротивление или проводимость источника, остаются включенными в схему.
Для случая постоянных источников напряжения и тока общая система уравнений (1.5.1), составленная на основании законов Ома и Кирхгофа. Была приведена в § 1. Для случая синусоидальных источников энергии в (1.5.1) достаточно заменить активные сопротивления (R) комплексными (Z). Трудоемкость решения таких систем, в аналитическом виде тем больше, чем выше ранг системы. Поэтому в электротехнике разработаны методы, позволяющие на основе физических свойств цепи упростить необходимые расчеты.
В этом параграфе рассмотрим подробно наиболее важные методы расчета цепей: метод контурных токов, метод узловых напряжений,
метод суперпозиции, а также эффективный метод для случая, когда необходимо знать ток или падение напряжения только для одной ветви:
метод эквивалентного источника.
3.1. Метод контурных токов
Метод контурных токов основан на отказе от прямого вычисления токов ветвей из уравнений Кирхгофа. В этом методе в качестве неизвестных вводятся новые промежуточные контурные токи. На рис. 3.1.1 выделена часть цепи с тремя близлежащими контурами. Контурные токи изображены изогнутыми стрелками. Удобно выбрать одно направление для всех контурных токов, например по часовой стрелке, как на рис. 3.1.1. Контурный ток входит и тут же выходит из любого узла. Поэтому закон токов Кирхгофа для контурных токов удовлетворяется автоматически и достаточно записать p – q + 1 уравнений
37
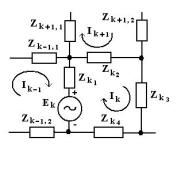
на основании закона напряжений Кирхгофа. Физические токи являются суперпозицией контурных токов, протекающих по конкретной ветви или элементу цепи. Например, так ток в ветви состоящей из сопротивления Zk2 определяется контурными токами Ik+1 и
Ik. Пусть он течет в сторону контурного тока Ik, тогда его определяют, как
IZ k 2 |
= Ik − Ik +1 . С |
математической |
|
||
стороны это является удобным выбором |
|
||||
замены переменных, который возможен |
|
||||
в силу линейности уравнений Кирхгофа |
|
||||
(независимости сопротивления, емкости |
|
||||
и |
индуктивности |
от |
величины |
|
|
протекающего тока). Однако найти |
Рис. 3.1.1 |
||||
такую |
математическую |
замену не |
|||
просто, |
тогда |
как |
физические |
|
|
рассуждения наглядно решают эту проблему. |
|
Запишем уравнение Кирхгофа для выделенного k-го |
контура на |
рис. 3.1.1 с использованием контурных токов |
|
Ek = Zk1 (Ik − Ik−1 ) + Zk 2 (Ik − Ik+1) + (Zk 3 + Zk 4 )Ik . |
(3.1.1) |
Это уравнение удобно преобразовать к каноническому виду
Ek = (Zk1 + Zk 2 + Zk 3 + Zk 4 )Ik − Zk1Ik−1 − Zk 2 Ik+1 . |
(3.1.2) |
Особенность этого уравнения заключается в том, что оно состоит из слагаемых, характерных для всех уравнений, записываемых на основании закона напряжений Кирхгофа для контурных токов. В таких уравнениях всегда присутствует слагаемое, определяющее падение напряжения на всех элементах контура, вызванное прохождением собственного контурного тока (первое слагаемое в уравнении (3.1.2)) и слагаемые, связанные с падением напряжения на элементах, по которым протекают еще и другие контурные токи (второе и третье слагаемое в уравнении (3.1.2)). Эти элементы одновременно входят как в выделенный контур, так и в другие контуры. В уравнения Кирхгофа эти последние слагаемые входят со знаком минус (см. уравнение (3.1.2)) при условии, что независимые контуры не перекрываются (как на рис. 3.1.1) и контурные токи выбраны текущими в одном направлении.
В общем случае уравнения Кирхгофа можно записывать двумя способами.
Первый способ основан на физическом принципе замены реальных токов в обычном уравнении Кирхгофа на суперпозицию из контурных токов, так как это было сделано при написании уравнения (3.1.1). В этом случае, падение напряжения на пассивном элементе равно произведению
38
комплексного сопротивления на сумму контурных токов, проходящих через данный элемент. Тогда
S |
S |
Zis (∑I )s , s (1, p −q +1) . |
|
∑E |
Eis =∑Z |
(3.1.3) |
ii
Вуравнении (3.1.3) суммирование проводится по всем ЭДС (SE) и по
всем комплексным сопротивлениям (SZ), входящим |
в контур. |
Сумма(∑I )s представляет собой сумму контурных токов, |
проходящих |
через элемент Zis. ЭДС Eis и контурные токи I берут со знаком “+” или “–” в зависимости от того, совпадают или не совпадают их направления с выбранным направлением обхода контура. При n независимых контуров получают систему уравнений из n независимых уравнений вида (3.1.3) ранга n. В рассматриваемом случае n = р – q + 1. Алгебраическими преобразованиями полученная система приводиться к каноническому виду.
Второй способ основан на прямой записи уравнений Кирхгофа для контура в каноническом виде (см. уравнение (3.1.2)). Им обычно пользуются при наличии практики в расчетах цепей. Система таких линейно независимых уравнений с рангом n имеет вид
|
E |
= Z I |
1 |
+Z |
I |
2 |
+ +Z |
I |
n |
|
|||||||
|
1 |
|
11 |
|
|
|
12 |
|
|
|
1n |
|
|
||||
E2 = Z21I2 +Z22 I2 + +Z2n In |
|
||||||||||||||||
................................................. |
(3.1.4) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Zn1I1 +Zn2 I2 + +Znn In |
|
||||||||||||||
En |
|
||||||||||||||||
или в матричном виде |
|
|
|
|
|
|
|
|
|||||||||
E |
|
Z |
|
|
Z |
|
...Z |
|
I |
|
|
|
|
|
|||
|
1 |
|
|
11 |
|
12 |
|
|
|
1n |
1 |
|
|
|
|
||
E2 |
|
Z |
21Z22 ...Z2n I |
2 |
|
|
|
(3.1.5) |
|||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
... |
|
................... ... |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En |
|
Zn1Zn2 ...Znn In |
|
|
|
|
|||||||||||
В системах (3.1.4) и (3.1.5) Ei – контурная ЭДС (алгебраическая сумма ЭДС, входящих в i-тый контур); Zii – собственное сопротивление i- го контура (сумма сопротивлений, входящих в i- й контур); Zik – сопротивление, входящее в контуры i и k. При отсутствии общего сопротивления у контуров в системе (3.1.5) записывают нулевой член. Если направление для всех контурных токов выбрано одинаковое, то при не перекрывающихся независимых контурах все Zik при i ≠ k входят в систему с отрицательным знаком, причем в силу Zik = Zki определитель системы симметричен относительно главной диагонали:
39
E1E2
...
En
|
|
Z11 − Z12 ... − Z1n |
||||
|
|
− Z12 |
Z22 ... − Z2n |
|||
|
|
|||||
|
= |
|
|
|
|
|
|
............................ |
|||||
|
|
− Z |
− Z |
2n |
... Z |
nn |
|
|
1n |
|
|
||
I1I2
...
In
. (3.1.5 а)
Ниже мы укажем, как выбираются такие независимые контуры. При выборе независимых контуров, частично состоящих из не перекрывающихся контуров, а частично из перекрывающихся, симметрия относительно главной диагонали также останется. Однако теперь общие сопротивления, входящие в перекрывающиеся контуры входят в систему (3.1.5) с положительным знаком. Отметим, что, хотя система (3.1.5) вытекает из системы (3.1.3) при использовании математических преобразований, получать её все же проще непосредственной записью канонических уравнений Кирхгофа для контурных токов.
Общее решение системы (3.1.5) может быть получено, например, методом Крамера:
|
Z11...Z1k −1E1Z1k +1...Z1n |
|
Z11Z12...Z1k ...Z1n |
|
|
|
|
Z21...Z2k −1E2Z2k +1...Z2n |
|
Z21Z22...Z2k ...Z2n |
|
1 |
n |
Ik = |
|
: |
............................ |
= |
|
∑Ei∆ik , (3.1.6) |
|
|
|||||
|
..................................... |
|
|
∆ i=1 |
||
|
Zn1...Znk −1EnZnk +1...Znn |
|
Zn1Zn2...Znk ...Znn |
|
|
|
где ∆ – определитель системы, ∆ik – алгебраические дополнения элементов Zik, в которых k соответствует номеру столбца, исключаемого из определителя системы.
Для записи систем (3.1.3), (3.1.5) необходимо уметь находить в цепи все независимые контуры. Основываясь на принципе, что независимые контуры отличаются друг от друга хотя бы одной ветвью, развиты два простых способа их нахождения.
Первый способ. Выбирают систему ветвей (дерево схемы), которая содержит все узлы, но не содержит ни одного замкнутого контура. Все независимые контуры получают поочередным присоединением к данному дереву новых ветвей.
Второй способ. Выбирают произвольный замкнутый контур. Все независимые контуры получают последовательным размыканием (отсоединением) одной ветви в предыдущем контуре и нахождением в оставшейся цепи нового замкнутого контура.
В теории графов доказывается, что найденное таким способом количество независимых контуров равно в точности p - q + 1. Первый способ более предпочтителен, так как при использовании его независимые контуры не перекрываются и получаемая система канонических уравнений
40
