Мищенко А. М. Лекции по электротехнике

Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Теоретические основы электротехники

Файл:

а напряжение на емкости

.pdf

Скачиваний:

151

Добавлен:

02.05.2014

Размер:

1.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Для определения искомого тока i1(t) достаточно найти постоянные С1 и С2. Решение системы дает С1 = 5 + j5, С2 = 5 – j5. Суммируя свободный ток с принужденным, получаем

i (t) =i		(t) +i	(t) =(5 + j5)e(−100+j100)t +(5 − j5)e(−100−j100)t +10 =
1	1св	1пр	(5.2.23)
=10
	2e−100t cos(100t +π 4) +10. A.

Остальные постоянные интегрирования и токи в оставшихся ветвях найдите самостоятельно.

Рассмотренный общий подход не всегда целесообразен. Иногда бывает проще последовательным исключением неизвестных свести систему уравнений к одному дифференциальному уравнению более высокого порядка. В нашем случае для нахождения i1 последовательная подстановка i2 из третьего уравнения во второе и i3 из второго в первое дает уравнение второго порядка

C L R	d 2i	+(CR R	+ L)	di	+(R	+ R )i	= E .
	1			1				(5.2.24)
	dt2
2		1 2		dt	1	2 1

Начальные условия так же, как и прежде для тока определяются током в индуктивности, а его первой производной – из первого уравнения системы (5.2.18).

Еще проще определить ток в сопротивлении R1 можно, применив метод контурных токов. В данной цепи два независимых контура. Пусть первый контур состоит из ветвей с источником и емкостью, а второй из ветвей с емкостью и сопротивлением R2. Тогда искомый ток будет контурным током первого контура. Система уравнений для контурных токов

= R1I1 +

∫0(I1 (t′) − I2 (t′))dt′+uC (0),

(5.2.25)

R2 I2 +

∫0(I2 (t′) − I1(t′))dt′+uC (0).

Начальные условия

I1(0) = E R2 ,

(0) = u

(0)

= (E − R1I1(0) −uC (0)) / L,

(5.2.26)

t =0

= (E / R

−u

(0) / R ) /(R C).

t =0

Первые два получены из независимых условий, а вторые из системы уравнений (5.2.25). Решение этой система проводиться одним из выше изложенных способов.

Пример 5.2.4. На рис. 5.2.4. приведена схема с источником напряжения

e(t) = E sin(ωt +ϕ) . Источник напряжения

работает на резонансной частоте ω = 1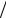LC .

Найдем ток i(t) в цепи после замыкания ключа. До момента коммутации при t = 0 ток в индуктивности

uC (−0) =−				E	cos(ωt +ϕ) =
uC (−0) =−			ω(R1 +R2 )C		cos(ωt +ϕ) =	(5.2.28)
		ρ	ω(R1 +R2 )C			(5.2.28)
=−E		ρ		cos(ωt +ϕ),
=−E	(R	+R )		cos(ωt +ϕ),
	(R	+R )
	1		2

R1 L

e(t)

Рис. 5.2.4

где ρ = 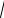L C . Поэтому независимые начальные условия: i(0) = iL(–0) и

uС(0) = uС(–0) . Величина ϕ соответствует фазе напряжения источника в момент коммутации. Запишем уравнение Кирхгофа для цепи после коммутации

e(t) = R i

+ L

+ u

(t),

(5.2.29)

C ∫

где u

(t) =

1 t

idt + u

(0) . Дифференцируя

уравнение Кирхгофа,

получаем дифференциальное уравнение второго порядка для тока:

L	d 2i	+ R	di	+	1	i = Eωcos(ωt +ϕ) .	(5.2.30)
	dt2				C
		2 dt

Начальными условиями для этого уравнения являются:1) тока i(0) и

2) первая производная	di	в первый момент после коммутации. Ток i(0)
	dt
		t=0

уже был найден из закона коммутации о постоянстве тока в

индуктивности. Значение же первой производной	di	(зависимое
	dt	t =0
	dt	t =0

начальное условие) найдем из уравнения Кирхгофа (5.2.29), используя i(0)

и uC(0),

(sinϕ −

sinϕ +

cosϕ) =

+ R

t =0

(5.2.31)

(R1 sinϕ + ρ cosϕ).

L(R1 + R2 )

Установившийся в цепи ток можно найти либо как частное решение дифференциального уравнения, либо прямым определением стационарного тока в цепи после коммутации. В последнем случае для нахождения установившегося тока можно использовать любой способ расчета, описанный в §3. В стационарном, установившемся режиме цепь так же, как и до коммутации будет находиться в состоянии резонанса, поэтому

iуст =	E	sin(ωt +ϕ) .	(5.2.33)
	R
	2

Свободный ток (iсв.) является решением однородного дифференциального уравнения. Для его нахождения необходимо сначала

решить характеристическое уравнение								p2 +	R2	p +ω2 = 0 . Корни этого
решить характеристическое уравнение								p2 +		p +ω2 = 0 . Корни этого
									L
уравнения:	p		= −		R		R2	В	зависимости от значения
уравнения:	p		= −		2 ±		2 −ω2 .	В	зависимости от значения
	1,2				2L		4L2
					2L		4L2
			R2
дискриминанта			2	−ω2		переходный процесс может развиваться либо с
дискриминанта			2	−ω2		переходный процесс может развиваться либо с
		4L

возникновением колебаний, либо без. Рассмотрим случай без возникновения колебательного возмущения тока. При этом будем полагать, что дискриминант равен нулю, т. е. R2 = 4ρ. В этом случае

	−	t
i = ( A + Bt)e	−
i = ( A + Bt)e	τ , где τ = 2L R .
св					2
Реальный ток в цепи
i(t) = i +i			= ( A + Bt)e−	t	+	E	sin(ωt +ϕ) .
	уст			τ		E		(5.2.34)
				τ				(5.2.34)
св						R2
						R2

Используя начальные условия для реального тока, получаем систему уравнений для нахождения констант А и В

		E				E
A +			sinϕ =				sinϕ,
A +		R2	sinϕ =			R1 + R2	sinϕ,
		R2				R1 + R2			(5.2.35)
	A			Eω			E		(5.2.35)
−	A	+ B +		Eω	cosϕ =		E		(R sinϕ + ρ cosϕ).
−	τ	+ B +			cosϕ =		L(R	+ R )	(R sinϕ + ρ cosϕ).
	τ			R			L(R	+ R )	1
				2			1	2

Решая данную систему относительно А и В и подставляя в выражение для реального тока (5.2.34), получаем ток в цепи после коммутации

i(t) =	R1E sinϕ			[t(τ−1 −ωctgϕ) −1]e−	t	+	E	sin(ωt +ϕ)
					τ
							R
	R	(R + R )
	2	1	2				2

Из сказанного следует, что классический метод является мощным инструментом расчета электрических цепей. «Недостаток» его связан с повышенным уровнем математической подготовки и большим объемом вычислений, связанных с нахождением постоянных интегрирования.

5.3. Расчет переходных процессов с использованием преобразования Лапласа

5.3.1*. Расчет переходных процессов решением дифференциальных уравнений Кирхгофа методом преобразования Лапласа.

Преобразование Лапласа, его свойства и применение в решении обыкновенных дифференциальных уравнений подробно рассмотрены в [4,5]. Идея метода заключается в переносе решения из области функций действительного переменного t в область функций комплексного переменного p = σ + jω, позволяющего вместо интегро-дифференциальных систем уравнений получать более простую для решения систему алгебраических уравнений. Полученное решение обратным преобразованием возвращают в область функций действительного переменного.

Переход к функциям комплексного переменного осуществляют с помощью прямого преобразования Лапласа

F( p) = ∫∞ f (t)e−pt dt .	(5.3.1)
0

Коммутация происходит при t = 0. Это преобразование, строго говоря, определяет F(p) в области значений p, для которых интеграл сходится, а именно в полуплоскости σ > a, где a – абсцисса сходимости. В другой же полуплоскости функция F(p) является аналитическим продолжением интеграла (за исключением особых точек – полюсов).

Определенную таким образом функцию F(p) называют изображением по Лапласу, а функцию f(t) – оригиналом. Выражение (5.3.1) обычно

F( p) = F1( p) F2 ( p)

разложения.

записывают			ˆ	записи
записывают	сокращенным способом L[F( p)]= f (t) . В такой			записи
прямое преобразование первой производной функции имеет вид
ˆ df (t)	= pF( p) − f (+0) ,			(5.3.2)
L	= pF( p) − f (+0) ,			(5.3.2)
dt
а интеграла –
t		F( p)
ˆ
L ∫f (t′)dt′ =			,	(5.3.3)
L ∫f (t′)dt′ =		p	,	(5.3.3)
		p
0

где F(p) – изображение по Лапласу функции f(t) а f(+0) – значение f(t) при t = +0.

Обратное преобразование Лапласа осуществляют с помощью интеграла

	1	c+ j∞
f (t) =		∫F( p)e pt dp ,	(5.3.4)
	2πj
		c− j∞

где c выбирается так, чтобы правее этой абсциссы отсутствовали полюсы

функции	ˆ−1	[F( p)]= f (t) . При
	F(p). Сокращенная запись (5.3.4) – L

вычислении интеграла путь интегрирования заменяется замкнутым контуром Гn , составленным из отрезка (a − jbn , a + jbn ) и части

окружности Cn' , расположенной слева от прямой Re p = a , согласно

лемме Жордана. Замена дает возможность применить теорему о вычетах, согласно которой оригиналом F( p) служит функция:

f (t) = lim	∑resF( p)e pt ,		(5.3.5)
n→∞	( Гn )	pk
	( Гn )
где сумма берется по всем особым точкам функции			F( p) , лежащей

внутри Гn .

Для нахождения оригинала по изображению используется теорема Пусть изображение имеет вид правильной дроби

пусть числитель и знаменатель не имеет общих корней.

Тогда положение полюсов изображения определяется корнями уравнения F2 ( p) =0 . При этом возможны два случая: а) все корни простые; б) некоторые или все корни кратные.

Случай простых корней. Расчет оригинала проводят по формуле

ˆ−1

F1( p)

( p)

f (t) = L

∑res

F2 ( p)

k =1

( p)

F1( pk )

= ∑ ( p − pk )

e pt

= ∑

( p)

k =1

p= pk

k =1 F2′( pk )

,(5.3.6)

e pk t

где сумма берется по всем n корням F2	( p) или F2′( p) =	dF2	( p)	. При
где сумма берется по всем n корням F2	( p) или F2′( p) =	dp		. При
		dp		p= pk
				p= pk

вычислении с помощью выражения в квадратных скобках сначала сокращают на множитель (p – pk), а потом производят подстановку p = pk.

Случай кратных корней. Пусть l – й корень имеет кратность m. Тогда вычисление оригинала проводят по формуле

ˆ−1	F1(p)		n		F1( p)		pt
f (t) = L			= ∑res			e		=
					F2 ( p)
	F2	(p) k=1		pk

n−m

F1(p)

F1( p)

n−m

F1( p)

= ∑res

ept + res

ept

= ∑ (p

− pk )

ept

(5.3.7)

F2 (p)

k=1

F2 (p)

pl F2 ( p)

k=1

p=p

dm−1

( p)

{(p − p )m

ept}

(p)

(m −1)! dpm−1

p=p

Как и в предыдущем случае, суммирование проводиться после сокращения на (p – pk), а дифференцирования после сокращения на (p – pk)m. В окончательные выражения подставляют соответствующие значения корня.

Для достаточно широкого класса функций существуют таблицы оригиналов и изображений, которые упрощают взаимные переходы от изображений к оригиналам и наоборот.

Расчет переходных процессов с применением преобразования Лапласа сводится к следующей последовательности действий:

1.Записывают уравнения Кирхгофа в интегро-дифференциальной форме с учетом независимых начальных условий (начальных токов в индуктивностях и начальных напряжений на емкостях).

2.Применяя преобразование Лапласа, переходят к алгебраическим уравнениям для изображений токов и напряжений.

3.Решают полученные алгебраические уравнения.

4.Применяя обратное преобразование Лапласа, находят оригиналы, т. е. искомые функции тока или узлового потенциала.

Таким образом, использование преобразований Лапласа является лишь математическим методом решения уравнений Кирхгофа. Расчет переходных процессов методом, основанным на использовании преобразования Лапласа, проще классического метода, так как не требует нахождения частного решения для установившегося процесса и проведения утомительных вычислений постоянных интегрирования. Однако эта простота обеспечивается лишь возможностью использования таблиц оригиналов и изображений, приводимых в математических

справочниках.

Пример 5.3.1. В качестве примера найдем ток в цепи, приведенной на

рис. 5.2.2 после размыкания ключа. Расчет проведем методом Лапласа и

сравним его с расчетом классическим методом. В начале необходимо

найти начальные значения тока в индуктивности и напряжения на

конденсаторе, которые возникли в первый момент после коммутации. Они

Рис. 5.3.1

являются независимыми начальными условиями и находятся по законам

коммутации.

Они

были

найдены

ранее

u0 = ER2

(R1 + R2 ) , а

i0 = E (R1 + R2 ) . Далее записывается уравнение Кирхгофа (это уравнение

(5.2.11)) и берется от него преобразование Лапласа

= RI ( p) + pLI ( p) − Li

( p) +

(5.3.8)

Полученное алгебраическое уравнение легко разрешается относительно

изображения тока

I ( p) =

E + pLi0 −u0

(5.3.9)

L( p2 + 2βp +ω02 )

где

квадратный

трехчлен

знаменателе

соответствует

характеристическому уравнению в классическом способе. Поэтому

полюсы изображения тока являются корнями характеристического

уравнения. Взятие обратного преобразования при тех же предположениях

приводит к тому же самому выражению для тока (5.2.17).

Таким образом, метод Лапласа позволил избежать нахождения

зависимых условий и постоянных интегрирования. Тогда как решение

характеристического уравнения проводиться как в классическом методе,

так и при использовании преобразования Лапласа. Поэтому здесь также

могут возникнуть уравнения третьего и более порядка решение, которых в

аналитическом виде не всегда возможно. Такие ситуации не редки при

расчетах разветвленных цепей.

5.3.2. Расчет переходных процессов операторным методом.

Операторный метод основан на

свойствах

преобразования Лапласа

(выражения

(5.3.1)

– (5.3.3)),

позволяющие заменить исходную схему

эквивалентной схемой изображений. В такой схеме, во-первых, все источники тока и напряжения согласно формуле (5.5.1) заменяют их изображениями. Во-вторых, индуктивности в силу свойства дифференцирования оригинала

ˆ	ˆ	diL (t)	= pLI ( p) −LiL (+0)	(5.3.10)
L[uL (t)]= L L		dt

заменяют не только на эффективное сопротивление pL, но и последовательно с ним в схему вводят идеальный источник напряжения с ЭДС, равной L iL(+0), где iL(+0) – ток в индуктивности в момент коммутации. Направление вводимой ЭДС совпадает с выбранным направлением тока в индуктивности. Емкость, имеющую начальное напряжение uC(+0), в силу свойства интегрирования оригинала

ˆ	ˆ		1 t	I ( p) u			C	(+0)
L[uC (t)]= L				i(t′)dt′+uC (+0) =	pC	+		p	(5.3.11)
		C ∫			pC			p
			0

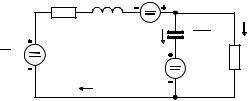
заменяют не только на эффективное сопротивление – 1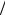 pC , но и последовательно с ним вводят идеальный источник напряжения с ЭДС, равной uC (+0) / p . Направление ЭДС в этом случае противоположно

выбранному направлению тока в емкости. Отметим, что эффективные сопротивления имеют такой же вид, как и в случае эффективных сопротивлений индуктивностей и емкостей при рассмотрении цепей синусоидального тока методом комплексных амплитуд. Только в данном случае вместо jω стоит p. Источник ЭДС и эффективное сопротивление

можно рассматривать, как операторную схему реального источника напряжения с внутренним сопротивлением равным эффективному сопротивлению. Поэтому, пользуясь правилом эквивалентности источников напряжения и источников тока, рассмотренным в § 1, индуктивность и емкость можно представлять и операторными схемами

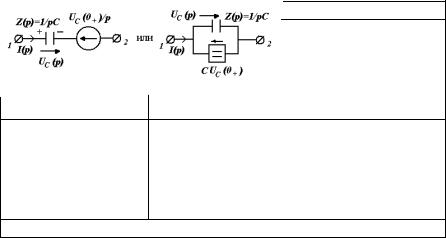
Исходная схема

Операторная схема

Рис. 5.3.1.

E(p)

Рис. 5.3.2

реальных источников тока. На рис. 5.3.1 приведены эквивалентные операторные схемы индуктивности и емкости, как в виде источника напряжения, так и в виде источника тока. Отметим, что при замене индуктивностей и емкостей на операторную схему источника тока необходимо помнить, о правилах расчета тока на внутренних сопротивлениях (см. § 1).

Таким образом, процесс введения начальных условий происходит автоматически с помощью эквивалентных операторных схем. Причем требуются только независимые начальные условия, определяемые по законам коммутации. В этих схемах элементы цепи выражены в операторной форме, а независимые начальные условия учтены введением в схему идеальных дополнительных источников напряжения и тока. Полученную схему рассчитывают одним из методов, приведенных в §3.

		Пример 5.3.1: Рассчитаем вначале схему,
R		приведенную на рис. 5.2.1. Будем полагать, что
		источник ЭДС является синусоидальным и в
K	pL	момент включения	(t = 0) имел напряжение
		e(0) = E0 sinψ , т.е.	реализуется второй случай

примера 5.2.1. Операторная схема приведена на рис. 5.3.2. В силу отсутствия начального тока в индуктивности вся замена ограничилась введением эффективного сопротивления индуктивности и обозначением ЭДС оригиналом E(p). Используя таблицу оригиналов и

изображений по Лапласу или беря интеграл (5.3.1), получаем оригинал ЭДС источника

∞

sin(ωt +ψ)e− pt dt =

E ∞

(e j(ωt +ψ) −e− j(ωt +ψ) )e− pt dt =

E( p) = E

∫

2 j ∫

e− jψ

+ωcosψ

e jψ

] = E

psinψ

[

−

2 j p − jω p + jω

p2 +ω2

Уравнение Кирхгофа для определения оригинала тока

p sinψ +ω cosψ

= (R + pL)I ( p)

p2 +ω2

. (5.3.12)

(5.3.12)

Решая его и используя таблицу оригиналов и изображений по Лапласу, или используя теорему о вычетах, получаем сразу туже самую зависимость (5.2.10).

Пример			5.3.2:		R1	pL	Li1(0)
Проведем			расчет		R1	pL	Li1(0)
переходных процессов								1
в	схеме	рис. 5.2.3.					I3(p)	1	I2(p)
в	схеме	рис. 5.2.3.		E			I3(p)	pC	I2(p)
Независимые				E				pC
начальные		условия		p			uC ( 0 )		R2
уже	найдены,		это			I1(p)	p
позволяет			сразу
составить
операторную			схему				Рис. 5.3.3
(см. рис. 5.3.3). Для
упрощения записи знак (+), указывающий на первый момент времени
после коммутации, опущен. Система уравнений Кирхгофа для тех же
самых контуров, но для оригиналов имеет вид

E	+ Li			(0)	−	I3 ( p)	= R I	( p) + pLI	( p) + uC (0)
	+ Li			(0)	−		= R I	( p) + pLI	( p) + uC (0)
			1			Cp	1 1	1	p
p		E				Cp			p
		E	+ Li1		(0) = R1I1( p) + pLI1( p) + R2 I2 ( p)
										(5.3.13)
		p								(5.3.13)
		p				I1( p) = I2 ( p) + I3 ( p)
						I1( p) = I2 ( p) + I3 ( p)

Решение этой системы проводят одним из алгебраических методов, например, методом Крамера или методом исключения. Для тока в сопротивлении R1 получаем

I1( p) =	(E −uC (0))CpR2 + E + Lpi1(0)					.	(5.3.14)
	p[CLR p2	+(CR R + L) p + R + R ]
	2	2	1	1	2

В знаменателе в квадратных скобках стоит левая часть характеристического уравнения для исходной, однородной системы уравнений Кирхгофа. Корни этого уравнения были уже найдены p1,2 = −100(1m j) .

Кроме этих корней знаменатель имеет еще один корень p3 = 0. Поэтому выражение для I1(p) имеет три различных полюса, и согласно теории вычетов

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Соседние файлы в предмете Теоретические основы электротехники

#
02.05.201410.02 Mб94Лекции по ТОЭ5.doc
#
02.05.20145.91 Mб63Лекции по ТОЭ6.doc
#
02.05.20146.61 Mб467Машины постоянного тока и трансформаторы.doc
#
02.05.20141.25 Mб82Методичка - Резистивные схемы.pdf
#
02.05.2014240.44 Кб37Методичка к курсовой работе.pdf
#
02.05.20141.8 Mб151Мищенко А. М. Лекции по электротехнике.pdf
#
02.05.2014829.16 Кб58Непопалов В.Н. Расчет линейных электрических цепей переменного тока.PDF
#
02.05.2014412.09 Кб44Непопалов В.Н. Расчет линейных электрических цепей переменного тока1.PDF
#
02.05.20144.08 Mб126Огорелков, Попов. Электротехника.doc
#
02.05.20144.08 Mб189Огорелков, Попов. Электротехника1.doc
#
02.05.2014308.22 Кб142Операционные усилители.doc