
Мищенко А. М. Лекции по электротехнике
.pdf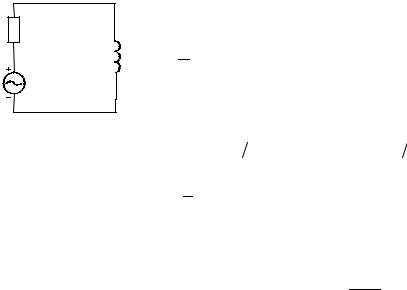
0 = uL |
2 |
+uC |
3 |
+uR +e2 (t) +e3 (t) −e1(t) . |
(1.3.6а) |
|||||
|
|
|
1 |
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
e1(t) −e2 (t) −e3 |
(t) = uL |
2 |
+uC |
3 |
+uR . |
(1.3.6б) |
||||
|
|
|
|
|
|
|
1 |
|
||
Пример 1.3.2. Интегрирование и дифференцирование на LC – цепочке.
Рассмотрим цепь, (рис.1.3.1) состоящую из сопротивления R, индуктивности L и источника напряжения e(t). Данная цепь может использоваться в качестве дифференцирующей и (или) интегрирующей цепочки, хотя обычно для этих целей используют цепочки из сопротивления и емкости. Цепочку с емкостью рассмотрите самостоятельно. Запишем уравнение Кирхгофа для этой цепи:
e(t) = Ri(t) +uL = Ri(t) + L di . |
|
|
(1.3.7) |
|||
|
|
dt |
|
|
|
|
|
|
Если в уравнении (1.3.7) основную роль |
||||
R |
|
играет второе слагаемое, то ток в цепи будет |
||||
|
пропорционален интегралу от ЭДС источника: |
|||||
e(t) |
L |
i(t) = L1 ∫e(t)dt . Физическая |
причина |
этого |
||
|
связана с тем, что резкие изменения |
ЭДС, |
||||
|
|
вызывая ответное изменение тока, приводят к |
||||
Рис. 1.3.2 |
|
появлению |
больших |
ЭДС |
самоиндукции. |
|
|
Характерное |
время изменения |
ЭДС источника |
|||
∆t не должно |
превышать отношения L R . |
Поэтому |
при ∆t < L R , |
|||
измеряя напряжение на сопротивлении, получаем интеграл от напряжения приложенного к цепочке uR = τ1 ∫e(t)dt , где τ = L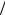 C . При обратном
C . При обратном
условии ∆t > τ , т. е. при более плавном изменении ЭДС источника, основную роль в уравнении (1.3.7) играет первое слагаемое и ток в цепи i(t) = e(t)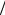 R . Поэтому, измеряя напряжение на индуктивности получаем
R . Поэтому, измеряя напряжение на индуктивности получаем
производную от напряжения, приложенного к цепочке uL =τ dedt(t) .
Рассмотрим случай линейного от времени изменения ЭДС источника:
e(t) = a t . |
|
Аналитическое |
решение |
уравнения |
(1.3.7) |
||||||
i(t) = |
at |
exp(− |
t |
) − |
aτ |
+ |
at |
. |
|
|
|
|
|
R |
|
|
|
|
|||||
|
R |
τ |
|
|
R |
|
|
|
|||
11
Первый случай ( ∆t <τ ). При t <τ |
экспонента раскладывается в ряд |
||||||||||
exp(− t |
τ |
) ≈1 |
− t |
τ |
+ |
1 |
( t |
τ |
)2 |
. Тогда |
напряжение на сопротивлении |
|
|
|
|
2 |
|
|
|
|
|||
uR ≈ (a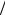 2τ)t2 и цепочка в этих условиях будет интегрирующей.
2τ)t2 и цепочка в этих условиях будет интегрирующей.
Второй случай ( ∆t >τ ). Тогда ( exp(− tτ ) <<1) и цепочка будет дифференцирующей. Напряжение на индуктивности uL (t) = aτ .
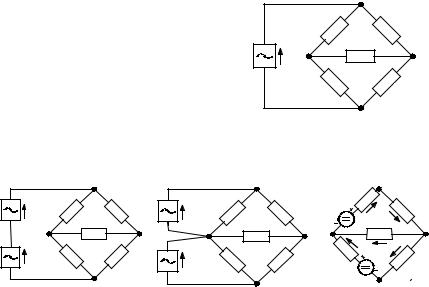
1.4. Условия эквивалентности представления реальных источников схемами источников напряжения и тока ограниченной мощности
При |
расчетах |
электрических |
цепей |
|
|
|||
эффективно используют взаимную замену схем |
R1 |
i(t) |
||||||
представления |
реальных |
источников |
|
|
||||
электрической |
энергии |
|
схемами |
источников |
|
|
||
напряжения и тока ограниченной мощности. |
e(t) |
u(t) |
||||||
Справедливость |
этого |
основывается |
на |
|||||
эквивалентности схем источников напряжения и |
|
|
||||||
тока ограниченной мощности. Схемы считаются |
|
|
||||||
эквивалентными, если замена одной на другую не |
Рис. 1.4.1 |
|||||||
изменяет |
напряжения, |
|
токи и мощности во |
|||||
внешней электрической цепи, присоединяемой к источникам. В этом смысле также считают эквивалентными сами
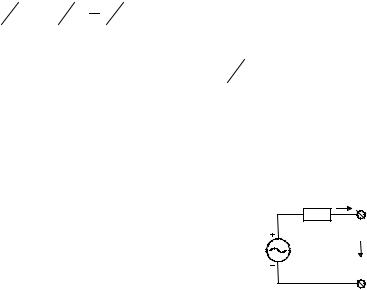
источники напряжения и тока ограниченной мощности. Условия эквивалентности рассмотрим для простого случая, когда пассивный внутренний элемент источников является резистором с сопротивлением R1 (рис. 4.1.1). Случаи, когда пассивный внутренний элемент является индуктивностью или емкостью, предлагается рассмотреть самостоятельно. Пусть этот источник нагружен на внешнюю цепь так, что на его клеммах
образовалось напряжение u(t) |
и через него потек ток i(t) . Тогда |
уравнение Кирхгофа |
|
e(t) = R1i +u(t) |
(1.4.1) |
В частности, при нулевом сопротивлении нагрузки (режим короткого замыкания) внутреннее сопротивление ограничит ток. Ток короткого
замыкания будет равен iкз(t) = e(t)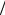 R1 . В случае бесконечного сопротивления нагрузки (режим холостого хода) ток равен нулю, а напряжение на клеммах источника равно ЭДС ( uxx (t) = e(t) ).
R1 . В случае бесконечного сопротивления нагрузки (режим холостого хода) ток равен нулю, а напряжение на клеммах источника равно ЭДС ( uxx (t) = e(t) ).
12

i(t)
 i1(t)
i1(t) 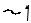 i0(t) R2
i0(t) R2  u(t)
u(t)
Рис. 1.4.2.
Заменим теперь эту схему представленияR1 i реального источника на схему источника
тока ограниченной мощности с внутренней |
|
e(t) |
u(t) |
проводимостью g =1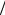 R2 (р
R2 (р ис. 1.4.2). Ток
ис. 1.4.2). Ток
во внешней цепи и напряжение на ней не должны изменяться от такой замены. По закону токов Кирхгофа ток во внешней цепи
i(t) = i |
(t) −i |
(t) = i |
(t) − u(t) |
(1.4.2) |
|
0 |
1 |
0 |
R2 |
|
|
|
|
|
|
|
|
Токи во внешней цепи не должны зависеть от представлений источников схемами, представленными на рис. 1.4.1 и 1.4.2. Поэтому, подставляя ток из уравнения (1.4.1) в уравнение (1.4.2), получаем
e(t) − u(t) = i |
(t) − u(t) |
(1.4.3) |
|
R1 |
0 |
R2 |
|
R1 |
|
||
Откуда следует, что выполнение равенства (1.4.3) при любых значениях напряжений на внешней цепи возможно лишь когда
R1 = R2 = R , e(t) = Ri0 (t) . |
(1.4.4) |
Эти равенства являются условиями эквивалентности представления реальных источников схемами, приведенными на рис. 1.4.1 и рис. 1.4.2. В частном случае короткого замыкания напряжение на источнике будет
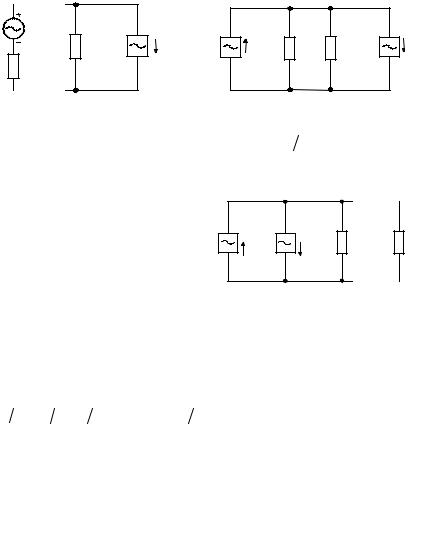
равно нулю, а ток короткого замыкания iкз(t) = e(t)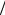 R1 = i0 (t) . В другом
R1 = i0 (t) . В другом
частном случае холостого хода (клеммы источника разомкнуты, и ток во внешнюю цепь не течет) напряжение холостого хода uxx (t) = Ri0 (t) = e(t) .
Выполнение условий (1.4.3) обеспечивает не только одинаковое напряжение и ток во внешней цепи, но и одинаковую потребляемую в ней мощность, тогда как формально рассчитанные мощности на пассивных внутренних элементах в различных схемах представления источника не равны. Это обстоятельство необходимо помнить во время расчетов схем при использовании эквивалентных замен источников тока на источники напряжений и наоборот.
На практике реальные источники в зависимости от соотношения между внутренним и внешним сопротивлением удобнее представить либо источником напряжения, если внутреннее сопротивление меньше внешнего, либо источником тока, если, наоборот, внутреннее сопротивление больше внешнего.
Случай, когда пассивные внутренние элементы могут состоять из произвольной комбинации емкостей, индуктивностей и резисторов, рассмотрите для цепей синусоидального тока после прочтения § 2.
13
Пример 1.4.1. Используем условия эквивалентности источников напряжения и тока, для определения токов в ветвях схемы, приведенной на рис. 1.4.3. Схема состоит из двух узлов, которые соединяют три параллельных ветви. Левая ветвь состоит их источника ЭДС и сопротивления, а правая из источника тока. Так как пассивные элементы состоят из резисторов, решение не будет зависеть от вида функций e(t) и i0(t). Расчет удобно начать с преобразования левой ветви в источник тока, считая сопротивление R1 внутренним сопротивлением. При этом в качестве внешней цепи будем рассматривать ветвь с сопротивлением R2, для этого на схеме выделим для наглядности узлы, относительно которых производится эквивалентное преобразование.
e(t) |
R2 |
|
|
i0(t) |
i1(t) |
R1 |
|
R2 |
i0(t) |
|
R1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
Рис. 1.4.3 |
|
|
|
Рис. 1.4.4 |
|
|
|||
На рис. 1.4.4 приведены результаты такого преобразования. Введенный |
||||||||||
идеальный источник тока дает ток |
i1(t) = e(t) R1 |
и |
его |
полярность |
||||||
совпадает с полярностью источника ЭДС (он создает ток по направлению, |
||||||||||
совпадающему с током который бы создавал во внешней цепи источник |
||||||||||
ЭДС). Переместим вдоль схемы источник тока i0 |
так, чтобы он был рядом |
|||||||||
с источником тока i1 (рис. 1.4.5). |
|
|
|
|
|
|||||
Это возможно, поскольку это всего |
|
|
|
|
|
|||||
лишь |
перестановка |
ветвей |
i1(t) |
i0(t) |
R1 |
R2 |
||||
относительно |
двух |
выделенных |
||||||||
узлов. |
Узлы, |
|
соединенные |
|
|
|
|
|
||
элементом |
(проводом), |
не |
|
Рис. 1.4.5 |
|
|
||||
имеющим |
|
сопротивления, |
|
|
|
|||||
считаются одним узлом, так как имеют одинаковый потенциал. Два |
||||||||||
параллельно включенных источника тока заменим одним источником. |
||||||||||
Полярность его выберем как у i1. Тогда i2 (t) = i1(t) −i0 (t) и схема имеет |
||||||||||
простой вид (рис. 1.4.6). Дальнейшие вычисления можно проводить двумя |
||||||||||
способами. По первому способу находим сначала общее сопротивление |
||||||||||
двух резисторов, руководствуясь правилом для параллельных соединений |
||||||||||
1 R0 =1 R1 +1 R2 |
и R0 = R1R2 (R1 + R2 ) . Затем находим напряжение на |
|||||||||
этом |
сопротивлении |
u(t) = R0i2 (t) . |
Это же напряжение будет и на |
|||||||
сопротивлениях R1 |
и R2. Отсюда находим ток через сопротивление R2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
14 |
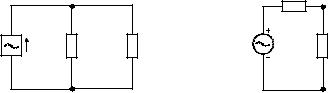
iR2 (t) = |
u(t) |
= |
R1 |
[ |
e(t) |
−i0 |
(0)] . Аналогичным образом найти ток в |
|
R2 |
R1 + R2 |
R1 |
||||||
|
|
|
|
|
сопротивлении R1 нельзя. Это связано с тем, что это сопротивление является внутренним сопротивлением источника напряжения, а при эквивалентной замене на источник тока обеспечивается неизменность тока и напряжения для внешней нагрузки. Поэтому надо вернуться к исходной схеме, изображенной на рис. 1.4.3, для которой теперь известно падение напряжения на сопротивлении R2 . По этой схеме ток в R1 найдем по закону Ома
iR (t) = e(t) −u(t) = e(t) − |
e(t) |
+ |
R1 |
i0 (t) = |
|
||||||
|
|
|
|||||||||
|
1 |
|
|
|
R1 |
R1 |
R1 + R2 |
R1 + R2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
R2 |
|
|
|
|
|
(1.4.5) |
= |
|
|
[ |
e(t) +i (t)] |
|
|
|
|
|
||
|
R |
+ R |
R2 |
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|||
|
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
R1 |
|
i2(t) |
R1 |
R2 |
e(t) |
R2 |
Рис. 1.4.6 |
|
Рис. 1.4.7 |
|
|
По второму способу в схеме на рис. 1.4.6 можно сделать относительно сопротивления R2 обратный переход от источника тока с внутренним сопротивлением R1 к эквивалентному источнику напряжения с ЭДС
e1(t) = R1i2 (t) . Тогда схема еще больше упростится (см. рис. 1.4.7). Ток в этой схеме равен току через сопротивление R2 в исходной схеме iR2 = e1(t)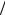 (R1 + R2 ) . Дальнейшие вычисления как по первому способу.
(R1 + R2 ) . Дальнейшие вычисления как по первому способу.
Преимущество расчетов с использованием взаимных эквивалентных замен источников напряжения на источники тока и наоборот связано с наглядностью и упрощением алгебраических вычислений, что важно при различных оценках.
1.5. Расчет токов ветвей на основании законов Ома и Кирхгофа
Расчет электрических цепей предполагает нахождение во всех ветвях токов и напряжений по заданным параметрам активных и пассивных элементов. Полная система уравнений для расчета, как токов, так и потенциалов записывается на основании закона токов Кирхгофа и закона Ома для ветви. Количество линейно независимых уравнений в системе должно равняться общему количеству неизвестных токов и неизвестных
15
потенциалов узлов. При наличии в цепи p ветвей и q узлов количество неизвестных равно p +(q −1) , так как потенциал одного узла можно
всегда приравнять нулю. Количество уравнений (1.3.4), записываемых по закону Ома для ветви равно количеству ветвей и они будут линейно независимы. Оставшееся q – 1 уравнение записывается на основании закона токов Кирхгофа для произвольного q – 1 узла. Эти уравнения также будут линейно независимыми. Действительно, если записать все уравнения по первому закону Кирхгофа для каждого узла, то ток каждой ветви войдет в одно уравнение со знаком “+” и в одно уравнение со знаком “–”, так как в один узел он втекает, а из другого – вытекает. Поэтому полная система из таких уравнений для всех узлов оказывается линейно зависимая: любое уравнение получается из суммы всех остальных после умножения ее на –1. Исключение же одного уравнения устраняет эту зависимость. Таким образом полная система уравнений для расчета цепей имеет вид:
∑r i (t) =0 ,
km
k
ui (t) −uk (t) =u0 j (t) mej (t),
m (1, q −1),
(1.5.1)
n = p.
Суммирование токов в первой группе уравнений проводится по всем ветвям (k), входящим в узел (m). Знак тока берется положительным, если он втекает в узел, и отрицательным, если он вытекает. Выбор знака при ЭДС во второй группе уравнений проводиться также как и при написании уравнения (1.3.4). Выражение для падения напряжения на пассивном элементе берется в зависимости от того, является ли он резистором, емкостью или катушкой индуктивности. Ранг системы уравнений (1.5.1) равен p + q – 1 . Эта система уравнений значительно упрощается при исключении во второй группе уравнений (взаимной подстановкой) q – 1 неизвестного потенциала узла и тем самым уменьшения их количества до p - q + 1 уравнения. Отметим, что получаемые такой подстановкой уравнения связывают некоторые суммы ЭДС источников с падением напряжения на пассивных элементах, т. е. получаются уравнения выражающие закон напряжений Кирхгофа. Поэтому для исключения таких длинных математических преобразований удобно сразу записывать систему уравнений на основании двух законов Кирхгофа. Ранг такой системы будет равен p, т, е количеству неизвестных токов:
16
r |
|
m (1, q −1), |
∑ikm (t) = 0 , |
||
k |
|
|
S E |
SZ |
(1.5.2) |
∑eks (t) = ∑u0ks , |
s (1, p − q +1). |
|
|
k |
|
k |
|
|
Суммирование ЭДС проводится по всем идеальным источникам напряжений, входящих в выбранный контур s, а суммирование падений напряжений на пассивных элементах ведут по периметру этого контура. Знак ЭДС берут положительным, если он возрастает по направлению обхода контура, и отрицательным, если убывает. Полученная система уравнений состоит из интегро-дифференциальных уравнений, решение которых будет обсуждено в § 5 для случая переходных процессов, а в § 3 и 4 – для случая синусоидальных источников энергии. В этом параграфе ограничимся случаем цепей постоянного тока. Тогда система (1.5.2) преобразуется к виду
|
|
r |
|
|
∑Ikm = 0 , |
m (1, q −1), |
|
|
|
k |
(1.5.3) |
S E |
SZ |
||
∑Eks = ∑Rks Iks , |
s (1, p − q +1). |
||
|
k |
k |
|
Способы решения системы (1.5.3), состоящей из линейных алгебраических уравнений, рассматриваются в курсе линейной алгебры. Отметим лишь, что трудоемкость решения таких систем в аналитическом виде тем больше, чем выше ранг системы. Поэтому в электротехнике разработаны методы, позволяющие на основе физических свойств цепи упростить необходимые расчеты. Эти методы рассмотрены в § 3.
Для записи системы (1.5.2) или (1.5.3) необходимо уметь находить в цепи все независимые контуры. Основной принцип нахождения независимых контуров базируется на том, что независимые контуры должны отличаться друг от друга хотя бы одной ветвью. В § 3 приведены два способа их нахождения, сильно облегчающих задачу в случае сложных схем. В этом параграфе ограничимся лишь замечанием, что для сравнительно простых схем независимые контуры могут быть найдены без применения общих методов, а лишь на основании известного их числа.
17
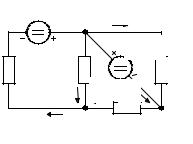
Пример 1.5.1. Пользуясь законами Кирхгофа, найдем токи во всех |
||||||||
ветвях схемы, изображенной на |
|
|
E1 |
|
i3 |
|||
рис. 1.5.1. Схема имеет пять ветвей |
|
|
|
|||||
и три узла. Обозначим токи по |
|
|
|
|
|
|||
номерам |
сопротивлений, |
а |
|
|
|
|
E2 |
|
последнему, |
текущему |
по |
|
R1 |
R2 |
|
R3 |
|
источнику ЭДС E2 присвоим пятый |
|
i4 |
||||||
номер. Направление токов выберем |
|
|
i2 |
i5 |
||||
так, как указано на рисунке. |
|
|
|
|
|
|||
Поэтому по закону токов Кирхгофа |
|
|
i1 |
|
R4 |
|||
можно записать |
два независимых |
|
|
|
||||
|
|
|
|
|
||||
уравнения. Выберем верхний и |
|
|
Рис. 1.5.1 |
|
||||
левый нижний узел. Тогда для |
|
|
|
|
i2 + i4 − i1 = 0 . |
|||
верхнего |
узла |
i1 −i2 −i3 −i5 =0 , |
а |
для |
нижнего |
узла |
||
Теперь найдем независимые контуры и запишем для них уравнения по закону напряжений Кирхгофа. Таких контуров должно быть три (5 – (3 – 1) = 3). Возьмем в качестве их следующие контуры: контур 1 состоит из ветвей с сопротивлениями R1 и R2; контур 2 образуется ветвями с сопротивлениями R2 и R4 и ветвью с источником E2; контур 3 – из ветвей с E2 и R3. Уравнения запишем, совершая обход всех контуров по часовой стрелке. Тогда полная система уравнений:
E1 = R1i1 + R2i2 |
|
|||||||
− E |
2 |
= −R i |
|
+ R i |
4 |
|||
|
|
|
2 2 |
|
4 |
|||
|
E2 = R3i3 |
|
|
|
(1.5.5) |
|||
|
|
|
|
|||||
|
0 |
= i |
− i |
− i |
− i |
|
||
|
0 |
|
1 |
2 |
|
3 |
5 |
|
|
= −i + i |
2 |
+ i |
|
||||
|
|
|
|
1 |
|
4 |
|
|
Решение этой системы уравнений можно проводить последовательной подстановкой, а можно и с применением правила Крамера, записав ее в матричной форме
|
E1 |
|
R1 R2 |
0 |
0 0 i1 |
|
|
|||
|
− E2 |
|
|
0 − R2 |
|
R4 0 |
|
|
|
|
|
|
|
0 |
i2 |
|
|
||||
|
E |
2 |
|
= |
0 0 |
R |
0 0 |
i |
|
(1.5.6) |
|
|
|
|
|
3 |
3 |
|
|
||
|
0 |
|
|
1 −1 |
−1 0 −1 |
i4 |
|
|
||
|
0 |
|
|
−1 1 |
0 1 0 |
i |
|
|
||
|
|
|
|
|
|
|
|
5 |
|
|
Тогда общее решение системы (1.5.6):
18
|
1 |
n |
|
|
ik = |
∑Ei∆ik , |
(1.5.7) |
||
∆ |
||||
|
|
i =1 |
|
где ∆ – определитель системы, ∆ik – алгебраические дополнения элементов. Проведя математические преобразования, получаем
i |
= |
|
E1(R2 + R4 ) − E2 R2 |
, i |
= |
E1R4 + E2 R1 |
, |
(1.5.8) |
|||||
|
|
|
|
|
|
||||||||
1 |
|
|
R1R2 |
|
2 |
|
R1R2 + R1R4 + R2 R4 |
|
|||||
|
|
|
+ R1R4 + R2 R4 |
|
|
||||||||
i |
= |
E2 |
, |
i |
= − |
E2 (R2 + R1) |
|
(1.5.9) |
|||||
|
|
||||||||||||
3 |
|
|
R3 |
4 |
|
R1R2 + R1R4 |
+ R2 R4 |
|
|||||
|
|
|
|
|
|
||||||||
При написании системы (1.5.1) необходимо все источники тока заменить эквивалентными источниками напряжения. При этом следует помнить, что токи и напряжения на внутренних элементах источников надо рассчитывать по исходной схеме. Однако возможны ситуации, когда идеальный источник тока является ветвью в цепи и его невозможно сразу заменить на эквивалентный источник напряжения. Эти ситуации рассмотрены в § 3 при обсуждении общих методов расчета цепей. Тем не менее и в таких ситуациях можно осуществить эквивалентные преобразования цепи позволяющие использовать уравнения Кирхгофа.
Рассмотрим это на примере схемы приведенной на рис. 1.5.2. |
|
|||||||
Пример 1.5.2. Найти все токи в |
|
|
|
|||||
ветвях схемы приведенной на рис. 1.5.2, |
|
R1 |
R2 |
|||||
используя законы Кирхгофа. |
|
|
|
|||||
В |
этой |
схеме |
невозможно |
прямо в |
I0 |
R5 |
|
|
ветви |
заменить |
источник |
|
тока |
|
|
||
источником напряжения. Однако, если |
|
|
|
|||||
представить |
источник тока |
в |
виде |
|
R4 |
R3 |
||
последовательно |
соединенных |
двух |
|
|||||
|
|
|
||||||
одинаковых источников тока, то схема |
|
Рис. 1.5.2 |
|
|||||
допускает |
|
последовательные |
|
|
||||
эквивалентные |
преобразования |
|
|
|
||||
приведенные на рис. 1.5.3. |
|
|
|
|
|
|||
|
R1 |
|
R2 |
|
R1 |
R2 |
R1 |
R2 |
|
|
I0 |
E1 |
|||||
I0 |
R5 |
|
R5 |
|
R5 |
|
||
|
|
|
|
|
|
|||
I0 R4 |
|
R3 |
I0 R4 |
R3 |
R4 |
R3 |
||
|
|
а) |
|
|
|
|
E2 |
|
|
|
|
|
б) |
|
в) |
|
|
|
|
|
|
|
|
|
|
|
19
Рис. 1.5.2
Эквивалентность преобразования схемы, приведенной на рис. 1.5.2 а, к схеме, приведенной на рис. 1.5.2 б, обеспечивается выполнением закона токов Кирхгофа для узла соединения сопротивлений R1 и R4. Поэтому токи в сопротивлениях R1, R4 и R5 не меняются, а, следовательно, не меняются и потенциалы в узлах. Переход к схеме, приведенной на рис. 1.5.2 в осуществляется обычным преобразованием источников тока в
эквивалентные источники напряжения |
с E1 = I0 R1 и E2 = I0 R4 . |
Дальнейшие вычисления |
|
Проводятся обычным способом. Расставляются направления токов и записывается система уравнений
i |
+i |
−i |
= 0, |
|
|
|
4 |
|
5 |
1 |
|
|
|
E1 = R1i1 + R2i2 + R5i5 , |
(1.5.10) |
|||||
E |
2 |
= R i − R i + R i . |
|
|||
|
|
4 4 |
5 5 |
3 3 |
|
|
Решив эту систему, находят токи во всех сопротивлениях в схеме приведенной на рис. 1.5.2 в. Эти токи соответствуют токам в исходной схеме только для сопротивлений R2, R3 и R5. В сопротивлениях R1 и R4 токи необходимо найти по исходной схеме, используя закон тока Кирхгофа и
вычисленные токи в R2, R3 и R5, т. е. i1 = i2 − I0 и i3 = i4 + I0 .
20
