
1.3. Преобразование Гивенса
Преобразование Гивенса определяется матрицами плоских вращений вида
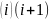
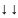
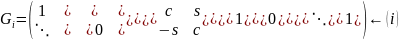 (1.3.1)
(1.3.1)
Матрица
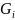 при фиксированном
при фиксированном
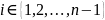 отличается от единичной
-матрицы
отличается от единичной
-матрицы
 лишь тем, что в
лишь тем, что в
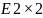 -подматрица
-подматрица
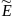 .
Занимающая клетку, образованную
пересечением
-х
и
.
Занимающая клетку, образованную
пересечением
-х
и
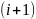 -х
строк и столбцов, заменяется подматрицей
-х
строк и столбцов, заменяется подматрицей
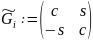
С
элементами
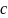 и
и
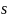 ,
удовлетворяющими условию
,
удовлетворяющими условию
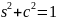 . (1.3.2)
. (1.3.2)
С
этим условием нормировка матрица
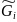 и соответственно матрица
являются ортогональными и, кроме того,
оправдывают название выполняемого
посредством
преобразования – преобразования
плоских вращений, поскольку
элементы
и
можно интерпретировать как косинус и
синус некоторого угла преобразования
поворота.
и соответственно матрица
являются ортогональными и, кроме того,
оправдывают название выполняемого
посредством
преобразования – преобразования
плоских вращений, поскольку
элементы
и
можно интерпретировать как косинус и
синус некоторого угла преобразования
поворота.
Имя
возможность наложить еще одно условие
на
и
в преобразовании Гивенса, распорядимся
этой свободой так, чтобы с помощью
последовательности таких ортогональных
преобразований матрицами
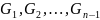 вида (1.3.1) матрицу Хесенберга
вида (1.3.1) матрицу Хесенберга
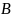 удалось привести к правому треугольному
виду, последовательно аннулируя
поддиагональные элементы в первом,
второй, …,
удалось привести к правому треугольному
виду, последовательно аннулируя
поддиагональные элементы в первом,
второй, …,
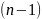 -м
столбцах.
-м
столбцах.
С
этой целью предположим, что уже сделаны
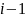 таких
шагов, в результате чего получена матрица
таких
шагов, в результате чего получена матрица
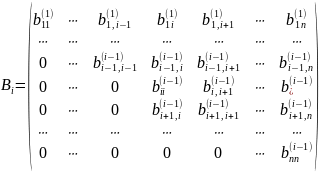
Найдем
произведение матрицы
на матрицу
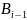 полагая в
из (1.3.1)
полагая в
из (1.3.1)
 .
Приходим к матрице с измененными
элементами по сравнению с матрицей
только в -й и в
-строках.
Потребуем, чтобы единственный ненулевой
поддиагональный элемент
.
Приходим к матрице с измененными
элементами по сравнению с матрицей
только в -й и в
-строках.
Потребуем, чтобы единственный ненулевой
поддиагональный элемент
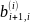 -го
столбца матрицы
-го
столбца матрицы
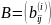 обратился в нуль, т.е. подберем числа
обратился в нуль, т.е. подберем числа
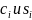 ,
связанные, согласно (1.3.2) соотношением
так, что
,
связанные, согласно (1.3.2) соотношением
так, что
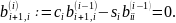
Отсюда получаем
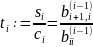 (1.3.3)
(1.3.3)
-
значение тангенса угла
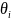 поворота в плоскости, определяемой -м
и
-м
ортами.
поворота в плоскости, определяемой -м
и
-м
ортами.
Очевидно,
что если на -м шаге окажется
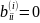 ,
то можно принять
,
то можно принять
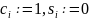 ,
т.е. положить
,
т.е. положить
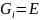 .
В противном случае, учитывая (1.3.1),
вычисляем
по формулам:
.
В противном случае, учитывая (1.3.1),
вычисляем
по формулам:

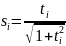
Предварительно
подсчитав
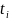 с помощью (1.3.3). После пересчета диагональных
и стоящих правее них элементов -й и
-й
строк по формулам
с помощью (1.3.3). После пересчета диагональных
и стоящих правее них элементов -й и
-й
строк по формулам
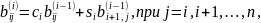
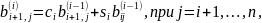
Матрица
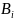 будет готова к выполнению следующего
шага преобразований Гивенса.
будет готова к выполнению следующего
шага преобразований Гивенса.
Таким
образом совокупность этих формул, в
которых натуральной переменной
последовательно придаются значения
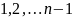 ,
полностью определяет процесс приведения
матрицы Хессенберга
,
полностью определяет процесс приведения
матрицы Хессенберга
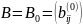 к матрице правой треугольной формы,
осуществляемый преобразованиями
к матрице правой треугольной формы,
осуществляемый преобразованиями
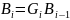 .
.
Практические применения
2.1. Метод отражений решения слау
Одним из возможных приложений полученного способа разложения квадратной матрицы в произведений ортогональной и треугольной матриц является метод решения систем линейных алгебраических уравнений, носящий название метод отражений.
Пусть дана система
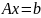 (2.1.1)
(2.1.1)
С
вещественным вектором правой части
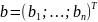 ,
вектором неизвестных
,
вектором неизвестных
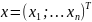 и вещественной матрицей коэффициентов
и вещественной матрицей коэффициентов
Рассмотрим две ситуации.
Предположим, что уже известно ортогональное разложение матрицы :
, (2.1.2)
Где -ортогональная, а - правая треугольная матрицы. Тогда после его подстановки в (2.1.1) имеем эквивалентную систему
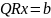
Которая, в свою очередь, ввиду ортогональности симметричной матрицы , равносильна системе
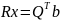 . (2.1.3)
. (2.1.3)
Обозначив
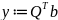 систему (2.1.3) можно переписать в виде
систему (2.1.3) можно переписать в виде
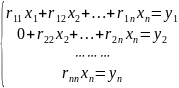 (2.1.4)
(2.1.4)
Из чего следует, что для получения искомого решения теперь достаточно выполнить обратный ход метода Гаусса.
Будем теперь исходить из того, что готового QR-разложения матрицы нет и, вообще говоря, оно в явном виде не требуется ,а нужно получить решение системы (2.1.1), используя преобразование отражения.
Промежуточной
целью здесь опять является приведение
данной СЛАУ к виду (2.1.4),
служащему стартовым для обратного хода
метода Гаусса. Это означает, что
одинаковыми преобразованиями, сохраняющими
эквивалентность систем, матицу
нужно привести к верхней треугольной
матрице
,
а вектор
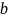 -
к вектору
-
к вектору
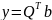 ,
где
и
отвечают представлению (2.1.2) В другие
терминах – расширенную матрицу
,
где
и
отвечают представлению (2.1.2) В другие
терминах – расширенную матрицу
 системы (2.1.1) ортогональными преобразованиями
нужно перевести в расширенную матрицу
системы (2.1.1) ортогональными преобразованиями
нужно перевести в расширенную матрицу
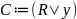 системы (2.1.3). Ясно, что это можно сделать,
применяя последовательно к столбцам
матрицы
преобразования Хаусхолдера по схеме
QR-факторизации.
системы (2.1.3). Ясно, что это можно сделать,
применяя последовательно к столбцам
матрицы
преобразования Хаусхолдера по схеме
QR-факторизации.
Действительно, так как
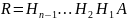 ,
,
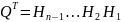
и,
значит,
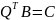 ,
то отсюда имеем следующее «технологичное»
представление
,
то отсюда имеем следующее «технологичное»
представление
 -матрицы
:
-матрицы
:
 ,
,
Где
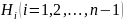 – матрица Хаусхолдера -го этапа.
– матрица Хаусхолдера -го этапа.
