
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра информатики
Пояснительная записка к курсовому проекту по дисциплине
«Методы численного анализа»
на тему «Ортогональное разложение матриц и его применения»
Выполнил: Бенько И.С.,
ст.гр. 852002
Принял: Хотеев А. Л.
Минск, 2010
Оглавление
1. Теоретические сведения 3
1.1 Преобразование Хаусхолдера. 3
1.2. QR-разложение матриц 4
1.3. Преобразование Гивенса 6
2. Практические применения 9
2.1. Метод отражений решения СЛАУ 9
3. Примеры и пояснение работы программы (язык C#) 11
3.1. Что реализовано в модулях программы? 11
3.2.Примеры работы программы 12
4. Решение СЛАУ методом отражений 13
4.1. Решение примера вручную 13
5. Список литературы 15
Теоретические сведения
В евклидовом n-мерном пространстве рассматриваются два ортогональных преобразования: преобразование отражения Хаусхолдера и преобразование плоских вращений Гивенса. В качестве примера применения преобразований Хаусхолдера изучается метод отражений для решения систем линейных алгебраических уравнений. Главный упор делается на использование ортогональных преобразований в задаче нахождения всех собственных числе (в том числе кратных и комплексны) произвольных квадратных матриц умеренных размеров с вещественными элементами.
Преобразование Хаусхолдера.
Пусть
w –
некоторый фиксированный вектор (столбец)
евклидова пространства
 со скалярным произведением
со скалярным произведением
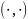 ,
такой, что
,
такой, что
 (1.1.1)
(1.1.1)
Образованная
с его помощью
 – матрица
– матрица
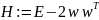 (1.1.2)
(1.1.2)
называется матрицей Хаусхолдера.
Чтобы
выявить простейшие геометрические
свойства преобразования
Хаусхолдера, осуществляемого
посредством матрицы
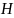 ,
посмотрим, что представляет собой вектор
,
посмотрим, что представляет собой вектор
 ,
служащий при этом преобразовании образом
произвольного вектора
,
служащий при этом преобразовании образом
произвольного вектора
 :
:
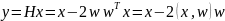 (1.1.3)
(1.1.3)
Если
взять
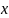 коллинеарным
коллинеарным
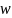 ,
т.е.
,
т.е.
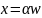 ,
где
,
где
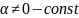 ,
то в силу (1.1.1), имеем
,
то в силу (1.1.1), имеем
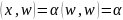 .
В таком случае, согласно (1.1.3),
получаем
.
В таком случае, согласно (1.1.3),
получаем
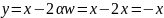
Если
же
перпендикулярно
,
то
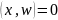 и, значит, из (1.1.3) следует, что
и, значит, из (1.1.3) следует, что
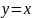 .
.
Итак, преобразование Хасхолдера действует на векторы -мерного евклидова пространства следующим образом: векторы, ортогональные определяющему матрицу Хасухолдера (1.1.2) вектору w, оно оставляет неизменными, а векторы, коллинеарные w, переводит в противоположные – отражает. Отсюда проистекают другие названия матрицы и соответствующего ей преобразования – матрица и преобразование отражения.
Непосредственным
перемножением вектора
на вектор
 находим:
находим:
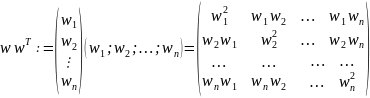
Очевидная
симметричность матрицы
 влечет симметричность матрицы
.
Пользуясь этим, имеем
влечет симметричность матрицы
.
Пользуясь этим, имеем

(поскольку
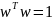 ,
в силу (1.1.1)). Полученное в итоге равенство
,
в силу (1.1.1)). Полученное в итоге равенство
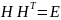 означает, что матрица
Хаусхолдера – ортогональная.
означает, что матрица
Хаусхолдера – ортогональная.
Одним из важнейших свойство ортогональных преобразований является сохранение длин преобразуемых векторов. Благодаря этому свойству, согласно вышепоказанному,, можно утверждать, что
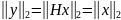 ,
,
 (1.1.4)
(1.1.4)
Равенство (1.1.4) играет существенную роль для конкретизации векторов при построении матриц Хаусхолдера, таких, чтобы преобразованиями с их помощью достичь определенных целей.
1.2. QR-разложение матриц
Поставим
теперь следующую задачу: ортогональными
преобразованиями привести
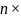 -матрицу
-матрицу
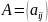 к треугольному виду. Иначе, осуществить
к треугольному виду. Иначе, осуществить
 -разложение
матрицы
-разложение
матрицы
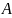 ,
т.е. описать процедуру, посредством
которой получается равенство
,
т.е. описать процедуру, посредством
которой получается равенство
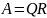 ,
,
Где
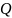 – ортогональная матрица, а
– ортогональная матрица, а
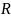 – правая треугольная.
– правая треугольная.
Будем решать эту задачу поэтапно.
На
первом этапе отдадим роль преобразуемого
вектора
в предыдущих рассуждениях и формулах
первому столбцу
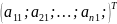 матрицы
.
Согласно им, построив матрицу Хасухолдера
матрицы
.
Согласно им, построив матрицу Хасухолдера с помощью вектора
с помощью вектора
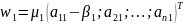
И скаляров
 ,
,
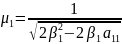
И применив ее к матрице , получим матрицу
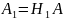
Со столбцом нулей под первым диагональным элементом, т.е. матрицу вида
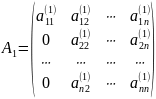
(где
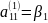 )
)
На
втором этапе нужно поступить таким же
образом с подматрицей матрицы
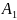 ,
которая получается вычеркиванием в
первой
строки и первого столбца. Легко проверить,
что это равносильно применению ко всей
матрице
преобразования Хаусхолдера, определяемого
формулами
,
которая получается вычеркиванием в
первой
строки и первого столбца. Легко проверить,
что это равносильно применению ко всей
матрице
преобразования Хаусхолдера, определяемого
формулами
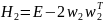 ,
,
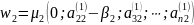
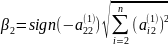 ,
,
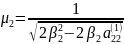
Для
этого достаточно лишь убедиться, что
матрица
 имеет структуру вида
имеет структуру вида
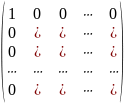
Означающего неизменность первых строки и столбца при выполнении преобразования
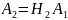
Результат первых двух этапов – это матрица
Ясно,
что для приведения данной
-матрицы
к треугольному виду потребуется
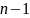 таких этапов, причем
таких этапов, причем
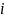 -й
этап определяется формулами:
-й
этап определяется формулами:
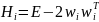
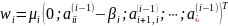
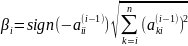 ,
,
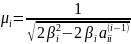
Итог всей процедуры из этапов – матрица треугольного вида
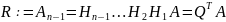
Где
через
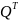 обозначена матрица, представляющая
собой произведение
ортогональных матриц Хаусхолдера
обозначена матрица, представляющая
собой произведение
ортогональных матриц Хаусхолдера
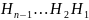 .
Так как произведением ортогональных
матриц является матрица, тоже ортогональная,
то равенство
.
Так как произведением ортогональных
матриц является матрица, тоже ортогональная,
то равенство
 можно обратить умножением слева на
можно обратить умножением слева на
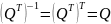 .
.
Теорема (о QR-разложении). Преобразованиями Хаусхолдера любая квадратная матрица с вещественными элементами может быть представлена в виде произведения вещественных ортогональной и правой треугольной матриц.
