А. Множества и операции над ними. Действительные числа.

Множества и действия над ними.

Множеством именуется некоторая совокупность элементов, объединенных по какому-либо признаку. Если есть такая совокупность, разумеется, как единое целое, говорят, что имеют дело с множеством. Приведенное определение не может рассматриваться как математически строгое, поскольку понятие множества является исходным, на основе него строятся остальные понятия математики. Тем не менее, из при веденного определения ясно, как можно говорить с множестве, например, действительных чисел или множестве плоских фигур. Если множество состоит из конечного числа элементов, оно называется конечным. Остальные множества называются бесконечными. Для множества используются следующие обозначения: А = {а,b,с,d}

Множество, в котором не содержится ни одного элемента, называется пустым. Обозначается оно знаком Ø.

Множества, состоящие из одних и тех же элементов, называют совпадающими. Например, совпадают два конечных множества, которые отличаются друг от друга порядком их элементов.

2. Отображения. Образ, прообраз, инъективность и сюръективность

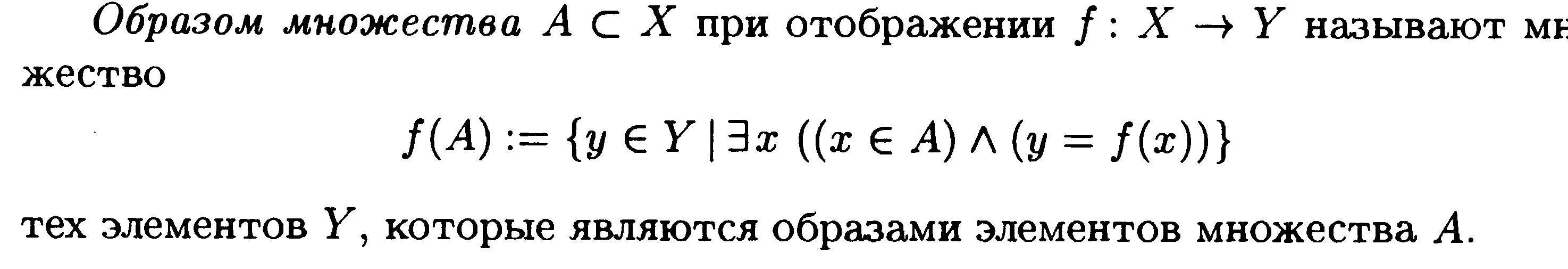
Отображение называется инъекцией, если для любых элементов x₁, x₂  X, для которых f(x₁) = f(x₂) следует, что x₁ = x₂. (рис. 7)

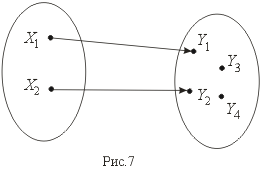
Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).

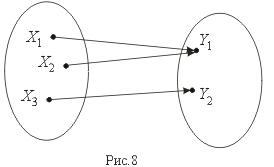
Биекция – это одновременно и сюръекция и инъекция (рис.9).

3. Мощность множества. Счетные множества и их свойства.

(определение счетного множества). Счетное  множество — это множество, эквивалентное множеству натуральных чисел.

Рассмотрим примеры счетных множеств.

Пример 11.

Множество всех целых чисел

Z = { 0, -1, 1, -2, 2, -3, 3,...,}.

Соответствие между целыми и натуральными числами можно осуществить по схеме

n  2n+1 при n 0, n  2|n| при n<0.

Множество всех четных положительных чисел. Соответствие по формуле n 2n.

Множество чисел 2ⁿ. Соответствие осуществляется по формуле n  2ⁿ.

Приведем некоторые свойства счетных множеств.

Теорема 1 (свойства счетных множеств).

-Всякое бесконечное множество содержит счетное подмножество.

-Сумма любого конечного или счетного множества счетных множеств есть счетное множества.

-Всякое подмножество счетного множества конечно или счетно.

4. Несчетные множества.

    Будем называть множество М несчетным, если оно бесконечно и если оно не эквивалентно множеству натуральных чисел (не эквивалентно любому счетному множеству).

    Это определение вводит понятие несчетного множества, не являющееся прямым отрицанием понятия счетного множества. В случае прямого отрицания в класс несчетных множеств попадают также и все конечные множества, так как никакое из них не эквивалентно множеству натуральных чисел. Введенные понятия удобнее, так как обычно рассматриваются только бесконечные несчетные множества.

    Теорема. Множество всех вещественных чисел отрезка является несчетным.

   Доказательство. Допустим противное, т.е. допустим, что множество вещественных чисел указанного отрезка счетно. Тогда все числа этого отрезка можно занумеровать в бесконечную последовательность при помощи натурального ряда чисел: x₁, x₂,_… , x_n,….

    Разобьем  отрезок  на три равные части и обозначим через ту из этих частей, которая не содержит число x₁. Далее отрезок также разобьем на три равные части и обозначим через ту из этих частей, которая не содержит число x₂ и так далее. Продолжая этот процесс, получим бесконечную последовательность отрезков , ,…, которая обладает тремя свойствами:

-каждый последующий отрезок последовательности вложен в непосредственно предыдущий и, значит, во все предыдущие;

-для всякого n N число x_n ;

-при возрастающем n  длина отрезка стремится к нулю.

    Применим  к этой последовательности отрезков теорему из анализа о вложенных отрезках. По этой теореме существует одно и только одно число c₀, которое принадлежит всем отрезкам последовательности. Это число удовлетворяет неравенствам: и значит оно находится среди чисел : x₁, x₂,_… .

  Пусть число c₀ имеет в последовательности x₁, x₂,_… номер k, т.е. c₀= x_k. Так как c₀= x_k, то c_k по построению последовательности отрезков. С другой стороны, c₀ есть общая точка всех отрезков последовательности отрезков и значит, c₀ . Полученное противоречие показывает, что сделанное допущение неверно и что множество есть несчетное множество. Теорема доказана.

5. Теорема о мощности множества всех подмножеств данного множества.

Конечное множество состоит из конечного числа эпементов, пусть их М штук.  Подмножеств, состоящих из 1 эл-та, будет М штук, из 2 эл-тов - число  сочетаний из М по 2, по 3 эл-та - будет число сочетаний из М по 3, и т. д.  Сюда еще включают "несобственные подмножества", а именно, пустое, и  всё множество А.  Всего получится сумма С(М,0)+С(М,1)+С(М,2)+...+С(М,М).  Известно, что такая сумма равна 2^M.  Примечание: Этот факт следует из формулы бинома Ньютона, так  как (1+1)^M=2^M.

6. Декартово произведение, бинарное отношение.

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А В. Таким образом  А В = {(x;y) | x A, y B}.

Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

Количество пар в декартовом прoизведении А В будет равно произведению числа элементов множества А и числа элементов множества В:   n(А В)=n(A) n(B).

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами.

Декартовым произведением множеств А , А ,…, A  называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А , вторая – А , …, n-ая – множеству А: А А … A .

Бинарным отношением между двумя множествами называется соответствие элементов одного из

них элементам второго.

Пусть даны два множества   и  , и пусть   - подмножество их декартова

произведения. Тогда тройка   называется бинарным отношением

между   и   Утверждение  обычно записывается в виде   и читается "  соотносится

с  " Если   то пишут   или

Бинарное отношение   называется

инъективным, если

полным слева, если

сюръективным (или полным справа), если

функциональным, если

функцией, если оно полно слева и функционально;

биективным, если оно полно слева и справа, а также инъективно и функционально.