
Устойчивость динамической системы
Рассмотрим динамическую систему
![]() .
(1)
.
(1)
Пусть эта система имеет решение
![]() ,
(2)
,
(2)
удовлетворяющее начальным условиям
![]() .
(3)
.
(3)
Пусть
![]() (4)
(4)
возмущенное движение, удовлетворяющее начальным условиям
![]() .
(5)
.
(5)
Невозмущенное
движение
![]() наз. устойчивым по Ляпунову,
наз. устойчивым по Ляпунову,
если
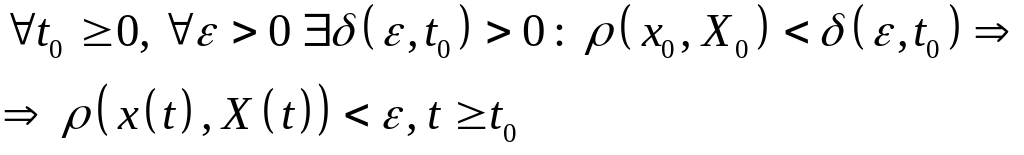 .
.
Обычно принимают
![]() ,
(6)
,
(6)
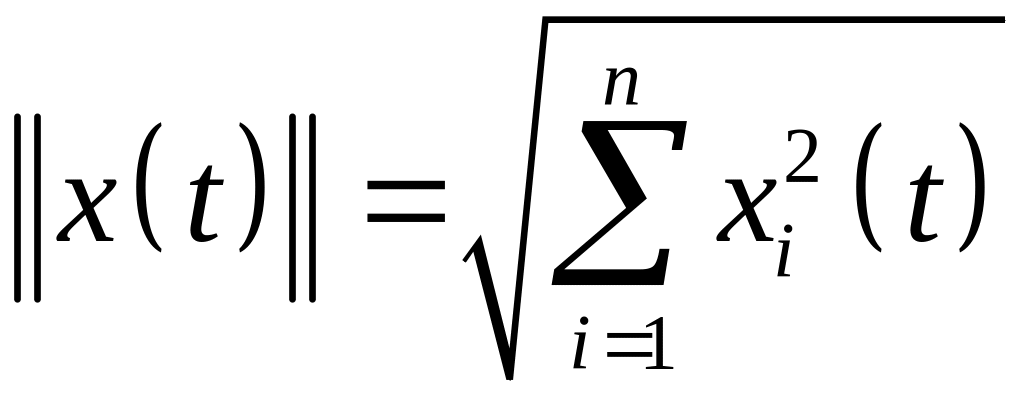 .
(7)
.
(7)
Выражение
(7) есть норма в пространстве
![]() .
.
Если используется чебышевская метрика для каждой компоненты решения, то определение устойчивости выглядит следующим образом:
![]() Невозмущенное
движение
наз. устойчивым по Ляпунову,
Невозмущенное
движение
наз. устойчивым по Ляпунову,
если
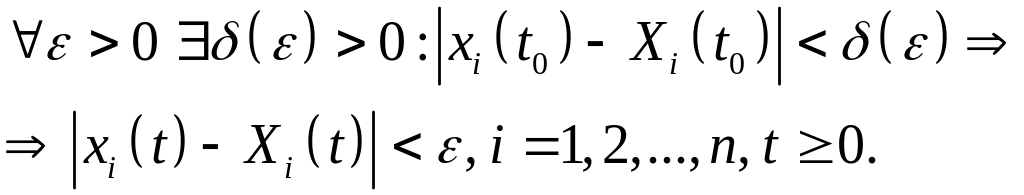
Устойчивость
по Ляпунову означает, что решения,
близкие по начальным условиям, остаются
близкими и при
![]() .
.
Если хотя бы одно неравенство из приведенных выше не выполняется
при
сколь угодно малом
![]() ,
то решение наз. неустойчивым по Ляпунову.
,
то решение наз. неустойчивым по Ляпунову.
Если
при
![]() расстояние
расстояние
![]() между возмущенным и невозмущенным
решениями стремится к нулю, то решение
наз.
между возмущенным и невозмущенным
решениями стремится к нулю, то решение
наз.
асимптотически устойчивым.
Устойчивость по Пуассону
Финитное
движение
![]() наз. устойчивым по Пуассону, если
наз. устойчивым по Пуассону, если
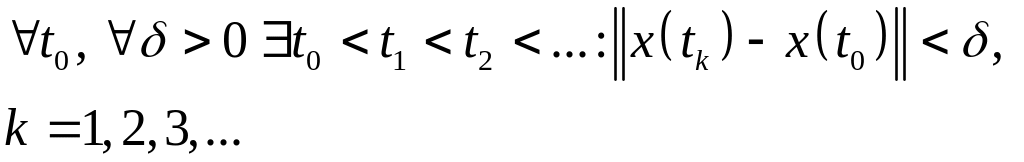
Устойчивость положения равновесия
Рассмотрим
точки
![]() ,
в которых
,
в которых
![]() .
(1)
.
(1)
Такие точки наз. положениями равновесия или стационарными точками или особыми точками динамической системы. Существует очевидное решение системы
![]() .
(2)
.
(2)
Положение равновесия может быть как устойчивым, так и неустойчивым. Из неустойчивого равновесия система в результате даже очень малых начальных отклонений может быть отброшена из стационарного состояния и движение станет либо достаточно сложным, либо перейдет в другое стационарное состояние, вообще говоря далекое от первоначального.
Пусть система
(3)
в
момент времени
![]() находится в состоянии
находится в состоянии
![]() ,
близком к состоянию равновесия
:
,
близком к состоянию равновесия
:
![]() ,
(4)
,
(4)
где
![]() - малый
- малый
![]() -
мерный вектор. В произвольный момент
времени
-
мерный вектор. В произвольный момент
времени
![]()
![]() .
(5)
.
(5)
Подставим (5) в (3). Получим
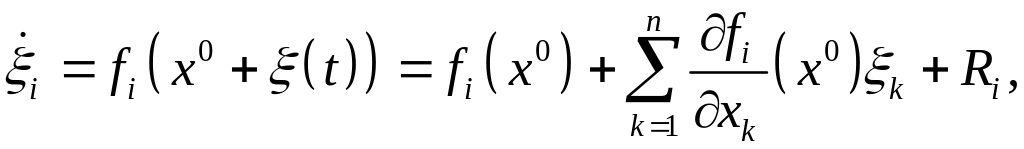 .
(6)
.
(6)
![]() .
.
Записано
разложение в ряд Тейлора. Так как
![]() ,
то получим систему дифференциальных
уравнений
,
то получим систему дифференциальных
уравнений
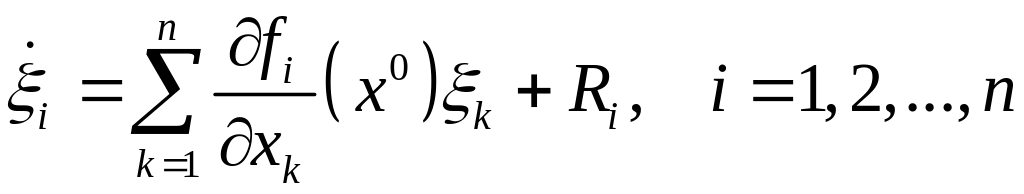 .
(7)
.
(7)
Если можно пренебречь нелинейными слагаемыми, то получим линейную систему
 .
(8)
.
(8)
Здесь
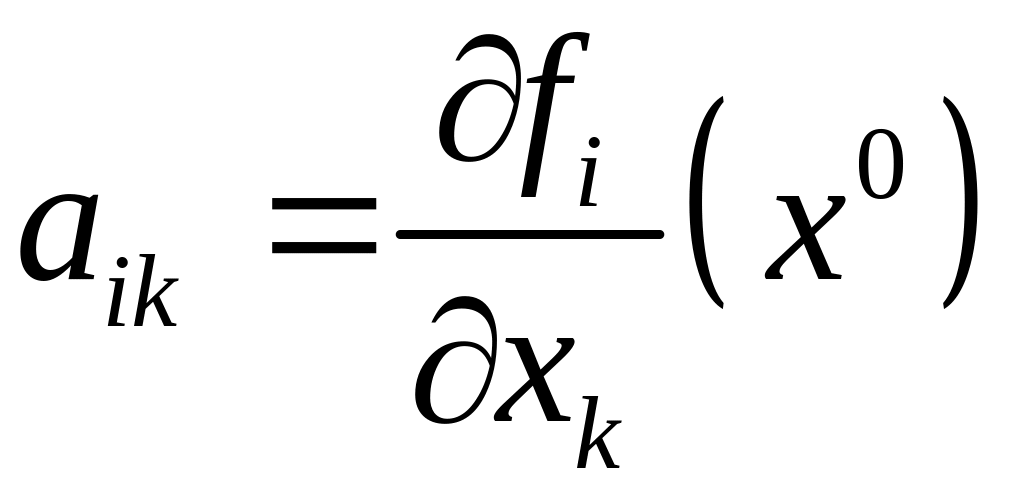 (9)
(9)
элементы
матрицы линеаризации, которую обозначим
через
![]() .
.
Теорема
Ляпунова утверждает, что если все СЗ
![]() матрицы
удовлетворяют неравенству
матрицы
удовлетворяют неравенству
![]() ,
(10)
,
(10)
то положение равновесия исходной системы асимптотически устойчиво. Если существует хотя бы одно СЗ, для которого
![]() ,
(11)
,
(11)
то
особая точка
является неустойчивой. Если же наряду
с СЗ с
встречаются и такие , для которых
![]() ,
то устойчивость положения равновесия
не может быть определена из анализа
линеаризованной системы.
,
то устойчивость положения равновесия
не может быть определена из анализа
линеаризованной системы.
СЗ определяются из уравнения
![]() .
(12)
.
(12)
Следовательно, изучение устойчивости сводится к анализу корней характеристического уравнения (12).
Иногда наряду с СЗ требуется знать СВ. Они определяются из алгебраических уравнений
![]() .
.
Критерий Рауса-Гурвица
Пусть характеристическое уравнение имеет вид
![]() .
(13)
.
(13)
Пусть уравнение (13) имеет корней
![]() .
(14)
.
(14)
Оценку расположения корней можно сделать, не решая уравнения (13).
Теорема Рауса-Гурвица
Для того чтобы все корни уравнения (13) имели необходима и достаточна положительность всех главных диагональных миноров так называемой матрицы Гурвица:
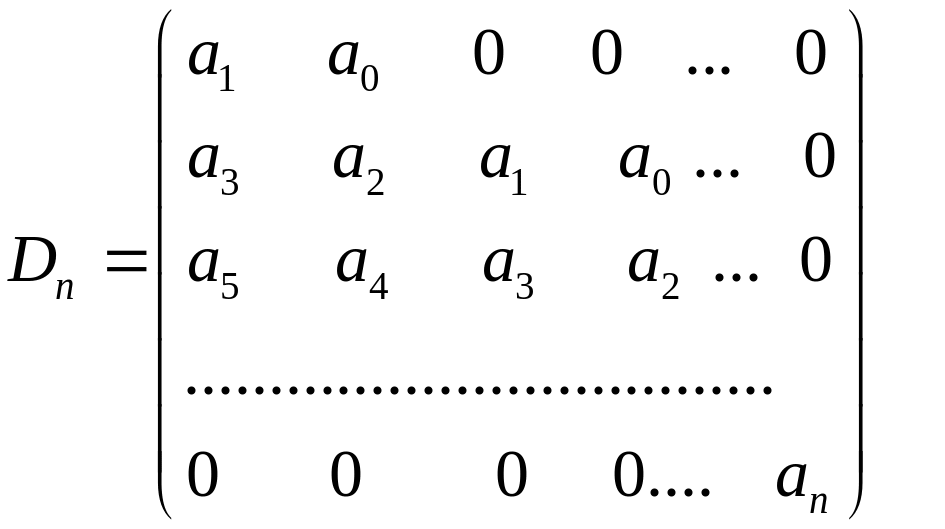 .
(15)
.
(15)
Структура
матрицы Гурвица такова: по главной
диагонали расположены коэффициенты
многочлена с
![]() до
до
![]() .
Столбцы содержат поочередно коэффициенты
только с нечетными или только с четными
индексами (включая
.
Столбцы содержат поочередно коэффициенты
только с нечетными или только с четными
индексами (включая
![]() ).
Все недостающие элементы (коэффициенты
с индексами, меньшими нуля или большими
)
заменяются нулями.
).
Все недостающие элементы (коэффициенты
с индексами, меньшими нуля или большими
)
заменяются нулями.
