1. Постановка задачи

Используя критерий Колмогорова, проверить, насколько справедливо предположение, что выборка интервалов времени безотказной работы изделий (таблица 2), полученная при их эксплуатации, случайна и взята из непрерывного распределения: Q(t) = 1 - exp(-t_б.р./T₀)

2. Сведения из теории

Общая характеристика метода. Статистической гипотезой называют всякое высказывание о генеральной совокупности, проводимое по выборке из этой совокупности. Статистические гипотезы классифицируют на гипотезы о законах распределения и гипотезы о параметрах законов распределения.

В общем виде задача проверки статистической гипотезы формулируется следующим образом. Имеем статистические данные в виде одной или нескольких выборок. Высказывается предположение о параметрах или законе распределения выборок. Это основное предположение называют нулевой гипотезой и обозначают H_О. Альтернативой исходной гипотезе H_О могут быть одна или две гипотезы H₁ и H₂. Таким образом, задача проверки гипотезы H_О для выборки, состоящей из n наблюдений Х₁, ... , Х_n случайной величины X, заключается в выработке определенных правил, по которым решаем принять гипотезу H_О или H₁ (H₂). Все возможное множество выборок объема n можно разделить на два непересекающихся подмножества S_n1 и S_n2. Если наша выборка (или ее характеристики, параметры) попадают в область S_n1, то принимается исходная гипотеза H_О, если же в область S_n2, то нулевая гипотеза H_О отвергается и принимается гипотеза H₁ (H₂). Подмножество S_n1 называют областью допустимых значений случайной величины, а S_n2 - критической областью. Выбор одной из областей однозначно определяет и другую область. Возникает необходимость формирования критериев, принципов или правил для построения критической области S_n2 или области допустимых значений S_n1.

При выборе критической области и принятии или отклонении гипотезы H_О по случайной выборке принятое решение соответствует истине с некоторой доверительной вероятностью.

При выборе критической области, приняв или отклонив нулевую гипотезу H_О, можно допустить ошибки двух видов. Ошибка первого рода с вероятностью α состоит в том, что отвергается верная гипотеза H_О и принимается конкурирующая гипотеза H₁ (H₂), что символически можно записать в следующем виде: α = P{(x₁, ..., x_n) Sn_n2 ‌ H₀}, то есть вероятность принятия гипотезы H₁ (H₂), когда на самом деле имеет место гипотеза H_О.

Ошибка второго рода с вероятностью β состоит в том, что принимается неверная гипотеза H_О, в то время как в действительности верна конкурирующая гипотеза H₁ (H₂), что символически записывается в виде:

β = P{(x₁, ..., x_n) Sn_n1 ‌ H₁}, то есть вероятность принятия гипотезы H_О, когда на самом деле имеет место гипотеза H₁(H₂).

В технической литературе вероятность α иногда встречается под названием «риск» поставщика, а вероятность β- под названием «риск» заказчика.

Существуют различного рода статистические гипотезы: о сравнении двух вероятностей отказа; об однородности двух выборок; о законе распределения случайной величины.

Вопрос о сравнении двух вероятностей отказа постоянно возникает при сравнении надежности однотипного оборудования, работающего одновременно в различных условиях, или одного и того же оборудования, но за разные периоды эксплуатации. Часто требуется сравнить надежность оборудования, проработавшего одинаковое время.

Задача проверки однородности выборок может возникать уже на начальной стадии исследования надежности изделия с целью их объединения и получения более весомой выборки. Если гипотеза об однородности выборок подтверждается, следовательно, обе выборки извлечены из одной и той же генеральной совокупности, а расхождение статистических данных является случайным и несущественным. Для проверки исходной гипотезы предлагается использовать критерий Смирнова, согласно которому величина наибольшего абсолютного расхождения D_m,n сравнивается с критическим значением этой статистики D_m,n (α) при заданном уровне значимости α.

Если окажется, что D_m,n < D_m,n (α), то гипотеза об однородности двух выборок не бракуется, если же D_m,n ≥ D_m,n (α), то основную гипотезу Н_О отвергают в пользу альтернативной гипотезы Н₁.

Определение законов распределения случайных величин по эксплуатационной информации. Известно, что для полной характеристики любой случайной величины необходимо знать ее закон распределения в виде функции распределения (в нашем случае вероятности отказа) или плот­ности вероятности. Определение закона распределения отказов (восстановлений) по опытным данным, т.е. по выборке, осуществляется в 3 этапа:

1. выбор предполагаемого вида закона распределения;

2. проверка согласия выборки с принятым законом распределения, т.е. согласованности опытного распределения с теоретическим;

3. оценка параметров выбранного закона распределения.

Выбор вида закона распределения. Подбор для данного статисти­ческого ряда теоретической кривой распределения и нахождения ее параметров в статистике называют выравниванием (сглаживанием) статистических рядов. Основой выравнивания является выбор вида тео­ретической кривой распределения. При принятии гипотезы о виде тео­ретического распределения главным является понимание характера причин утраты работоспособности данным видом оборудования. Други­ми словами, вид теоретического распределения, как правило, должен выбираться заранее из соображений, связанных с существом рассматри­ваемых явлений. Экспериментальными данными подтверждается хоро­шее соответствие процессов, приводящих к внезапным отказам, экспоненциальному закону распределения, процессов чистого износа — нормальному закону. Процессы усталостного разрушения, а также про­цессы, представляющие собой совокупность видов разрушения (устало­стного, износа внезапных изменений свойств объекта и др.), могут быть описаны распределением Вейбулла. При выборе теоретического зако­на распределения необходимо помнить, что для выявления статистиче­ски значимых различий законов распределения требуется весьма боль­шой объем информации, особенно для использования двух и более параметрических законов. Ориентировочно закон распределения можно выбрать по виду аппроксимации статистического ряда.

Проверка согласия опытного распределения с теоретическим. Вопрос о согласовании опытного и теоретического распределений является од­ним из важнейших вопросов проверки статистических гипотез. Между опытным и теоретическим распределениями всегда существуют расхож­дения. Возникает вопрос: объясняются ли эти расхождения только слу­чайными обстоятельствами, связанными с ограниченностью выборки n, или они существенны и связаны с тем, что подобранная теоретическая кривая плохо выравнивает данное опытное распределение. На практике для ответа на такой вопрос используются так называемые «критерии согласия»: критерий Колмогорова, критерий χ² критерий ω² и другие. Критерий Колмогорова может применяться для проверки любого теоретического распределения, однако при этом необходимо, чтобы гипотетическое распределение F(x) было известно заранее.

Алгоритм использования критерия согласия Колмогорова.

Как указывалось ранее, наиболее полной характеристикой надежности элементов является функция распределения времени безотказной работы (функция ненадежности) Q(t). При этом мы не затрагивали вопроса о том, откуда берется, как определяется этот закон. Ответ на этот вопрос один - из статистики отказов изделия, полученной по данным эксплуатации или эксперимента.

Исходным пунктом статистического исследования надежности любого электрооборудования является фиксация времени между отказами. По данным этой статистики составляется статистический (вариационный) ряд: t₁< t₂ < ... < t_k < ... < t_n, где n наблюдений случайной величины T (время наступления к-го отказа с момента начала наблюдений).

Имея статистический ряд, нетрудно построить статистическую функцию распределения случайной величины T, определяемую следующими неравенствами:

0 при t < t₁;

Q^*(t) = { k/n при t_k < t < t_k+1, 1 , k , n-1;

1 при t > t_n, 0

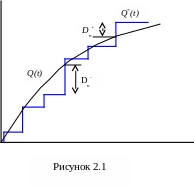
Статистическая вероятность отказа представляет собой прерывистую ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины T и по величине равны частотам этих значений (рис.2.1). Если каждое отдельное значение случайной величины T было наблюдено только один раз, то скачок статистической функции Q^*(t) в каждом наблюденном значении равен 1/n, где n - число наблюдений. При увеличении n статистическая функция Q^*(t) приближается (сходится по вероятности) к подлинной функции Q(t).

Примечание: Для невосстанавливаемых изделий под T следует понимать случайное время до первого отказа, а для восстанавливаемых - случайное время между отказами.

На практике мы почти никогда не имеем дела с большим числом наблюдений и вынуждены считаться с тем, что статистической функции Q^*(t) свойственны в большей или меньшей мере черты случайности.

Поэтому приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую существенные черты данного статистического ряда, но не случайности, связанные с недостаточным объемом экспериментальных данных.

Q(t)

1.0--------------------------------------------

0.9---------------------------------------------

0.8---------------------------------------------

0.7---------------------------------------------

0.6---------------------------------------------

0.5--------------------------------------------

0.4---------------------------------------------

0.3----------------------------------------------

0.2---------------------------------------------

0.1--------------------------------------------- t*10^-3

0 1 2 3 4 5 6 7 8 9 10 11 _час

Задача о наилучшем выравнивании (сглаживании) статистических рядов есть задача в значительной мере неопределенная, и решение ее зависит от того, что условиться считать "наилучшим". При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из соображений, связанных с физикой решаемой задачи.

Как бы хорошо ни была подобрана теоретическая кривая Q(t), между нею и статистическим распределением Q^*(t) неизбежны некоторые расхождения. Возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений n, или они являются существенными и связаны с тем, что подобранная кривая не адекватна данному статистическому распределению. Для ответа на такой вопрос служат так называемые "критерии согласия".

В качестве примера рассмотрим решение поставленной задачи с помощью критерия D_n Колмогорова.

В качестве меры расхождения между теоретическим и статистическим распределениями А.Н.Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения и соответствующей теоретической функцией распределения

D_n = max |Q^*(t) - Q(t)|.

Критерий Колмогорова намного проще других критериев, поэтому его весьма часто применяют на практике. При этом следует помнить, что этот критерий основан на индивидуальных значениях непрерывной случайной величины X в выборке объема n, а не группированных, поэтому при построении эмпирической функции распределения Q^*(t) недопустимо объединение статистических данных в разряды.

Если фактически найденное наибольшее расхождение D_n окажется больше или равно критическому значению статистики D_n (α), то, согласно критерию Колмогорова, с уровнем значимости α гипотеза H_О{M[Q^*(t)=Q(t)} должна быть отвергнута.

Критические значения для наибольшего отклонения эмпирического распределения от теоретического D_n(α) для n = 10…20…100 и

α = 0.01; 0.02; 0.05; 0.10 ; 0.20 приведены в табл. 6.2 [6].

Используется критерий по схеме:

1) по данным статистики составляется вариационный (упорядоченный) статистический ряд.

2) по статистическому ряду строится статистический интегральный закон (в виде ломаной кривой) Q^*(t).

3) высказывается гипотеза H_О о теоретической функции распределения Q(t) и строится ее график.

4)определяется статистика D_n.

5) по табл.6.2 [6] определяется критическое значение статистики D_n(α).

6) если D_n >= D_n (α), то с уровнем значимости α гипотеза H_О должна быть отвергнута.