Содержание соответствующего раздела в пояснительной записке

Данный раздел должен содержать:

краткие теоретические сведения,
исследование системы линейных алгебраических уравнений на совместность,
аналитическое решение системы линейных алгебраических уравнений методом Гаусса,
решение системы линейных алгебраических уравнений методом Жордана-Гаусса в системе MATLAB,
сравнение полученных результатов, найденных разными способами.

4. Приближенные методы решения нелинейных алгебраических уравнений

Необходимость отыскания корней характеристического уравнения всегда возникает при расчете переходного процесса в линейных электрических цепях. В общем случае характеристическое уравнение может быть сколь угодно высокого порядка. Значения, которые могут принимать корни характеристического уравнения дают представление о характере переходного процесса и в общем случае могут принимать комплексные значения.

Алгебраическое уравнение - ной степени задается в следующем виде:

Относительно небольшое количество задач отыскания корней нелинейных алгебраических уравнений можно решить аналитически, на практике почти всегда приходится находить решение уравнений с помощью численных методов.

Приближенное решение нелинейных алгебраических уравнений состоит из двух этапов:

этап отделения корней
этап уточнения корней

Пусть требуется найти корни уравнения . Этап отделения корней этого уравнения заключается в нахождении всех интервалов в области определения функции , на концах которых функция меняет знак. Количество интервалов определяется по числу корней. Не существует универсального метода, позволяющего отделить все корни нелинейного алгебраического уравнения. В качестве возможных способов отделения корней могут быть предложены следующие способы.

Графический способ. Приближенно строится график функции и по графику определяются интервалы на оси 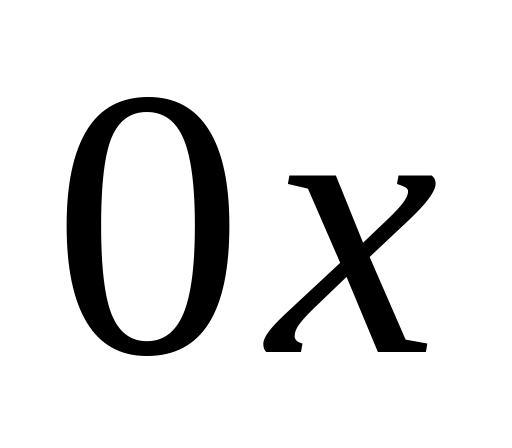, на которых функция меняет знаки.
Табличный способ. Строится таблица, состоящая из двух строк, в первой строке с каким-то произвольным шагом изменяется значение аргумента 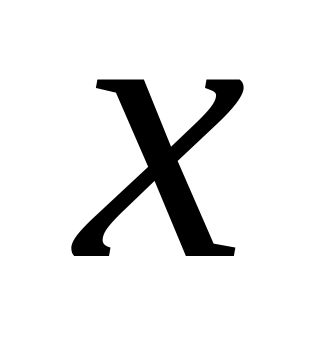, желательно на отрезке симметричном относительно . Во второй строке вычисляются соответствующие значения функции . Если в соседних ячейках второй строки функция меняет знак ( причем неважно с + на – или с - на +), то считается что на этом интервале находится хотя бы один корень.
Способ нахождения верхних и нижних границ положительных и отрицательных корней.

Метод деления отрезка пополам

После отделения корней можно уточнить его одним из методов последовательных приближений. Одним из таких методов является метод деления отрезка пополам. Этот метод является наиболее простым надежным методом уточнения корня на отрезке в том случае, когда функция из уравнения является непрерывной функцией и принимает на концах отрезка значения разных знаков, т.е. .

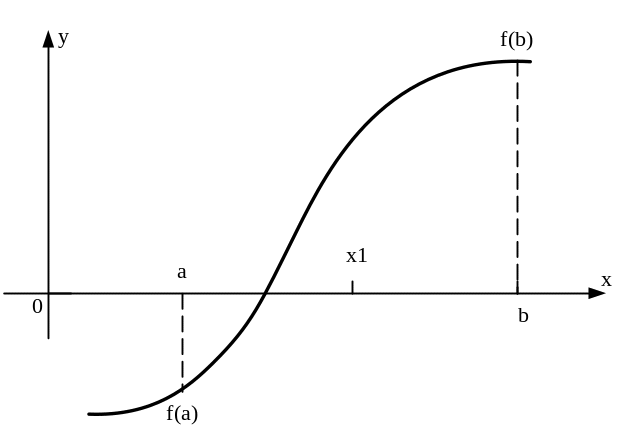
Рис. 4

Очевидно, что середина отрезка на рис. 4 служит приближением к искомому корню уравнения. Обозначим середину отрезка точкой . В этой точке определяется знак функции , затем выбирается та половина отрезка, на концах которой функция принимает значения разных знаков и деление повторяется по тому же самому алгоритму. Если требуется найти корень с точностью , то деление отрезка пополам продолжается до тех пор, пока длина последнего отрезка содержащего корень не станет меньше величины . Тогда середина последнего отрезка даст значение корня с требуемой точностью. В этом методе можно не вычислять само значение функции , достаточно лишь определить знак значения функции. Обозначим погрешность на шаге через , где - точное значение корня, тогда погрешности на - том и шаге связаны неравенством , где , что позволяет отнести метод деления отрезка пополам к методам, имеющим линейную скорость сходимости.