Задание для самостоятельного решения

1. Укажите базис, в котором матрица квадратичной формы 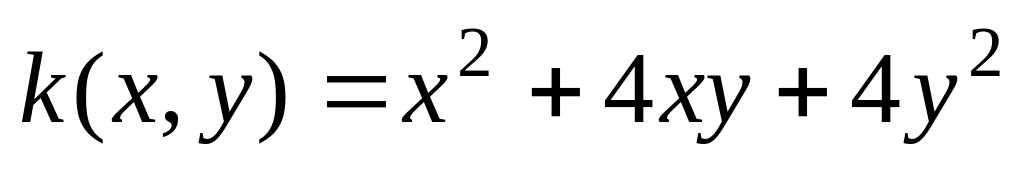имеет диагональный вид.

2. Приведите квадратичную форму 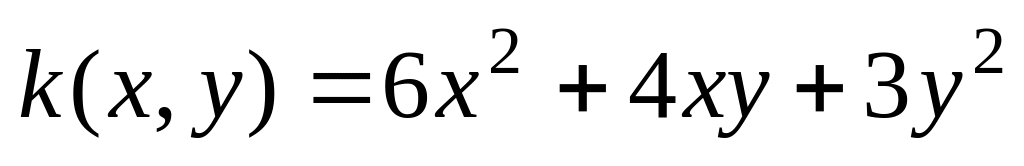к каноничес –

кому виду.

2.35.2. Приведение общего уравнения кривых второго порядка к каноническому виду

Рассмотрим общее уравнение кривой второго порядка:

(2.35.6)

Здесь  квадратичная форма,  линейная форма переменных . Более короткая запись уравнения (2.35.6) выглядит следующим образом:

(2.35.7)

где Аоператор с ненулевой матрицей

Если теперь выполнить поворот системы координат так, чтобы направления новых осей совпали с направлениями собственных векторов матрицы А, то вместо (2.35.6) получим уравнение

. (2.35.8)

Если , то путем параллельного переноса осей координат можно избавиться от линейной формы, выделив полный квадрат в суммах и . Тогда будем иметь

(2.35.9)

или (при )

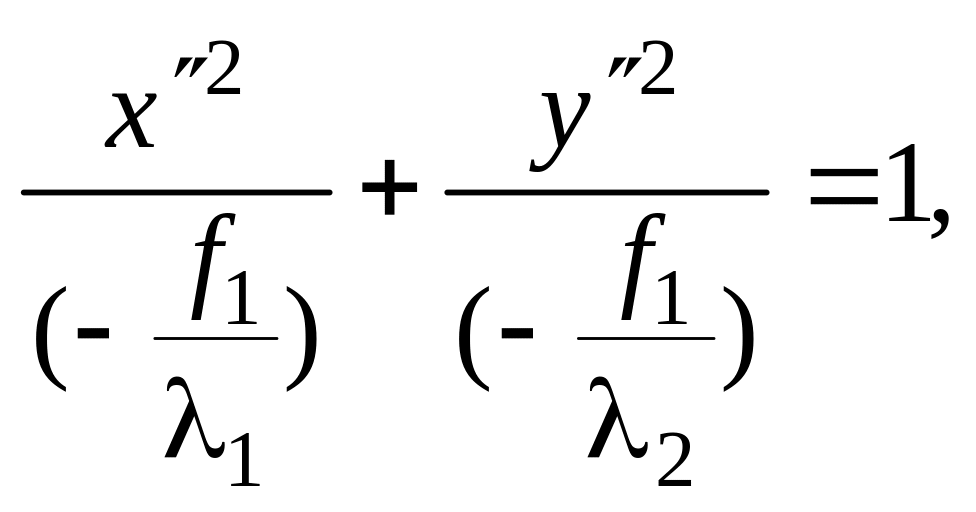(2.35.10)

где обозначено

И так, если , то общее уравнение кривой (2.35.6) приводится к виду (2.35.10). Свойства этой кривой существенно зависят от значений коэффициентов .

Если при этом , , то уравнение (2.35.6) определяет эллипс (рис. 2.22):

(2.35.11)

Здесь , (считаем также, что ). В случае получается уравнение окружности

.

Если знаки дробей и различны, то уравнение (2.35.6) определяет гиперболу (рис.2.23):

(2.35.12)

( для определенности в (2.35.12) считаем, что , ).

Если или (оба числа одновременно обратиться в ноль не могут) то общее уравнение кривой (2.35.6) можно привести к виду

или

. (2.35.13)

Уравнения (2.35.13) являются уравнениями параболы (рис.2.24 а,б).

При всех других значениях коэффициентов уравнение (2.35.9), а вместе с ним и (2.35.6), никаких других кривых не определяет. Нетрудно убедиться в том, что оно либо «вырождается» в точку ,либо в пару прямых , либо в одну прямую (например, при ), либо вообще не имеет геометрического образа (например, при ).

Т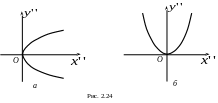 аким образом, общее уравнение кривой второго порядка может быть сведено к одному из канонических уравнений (2.35.11)  (2.35.13) переходом к новой системе координат, получающейся из старой посредством поворота и параллельного переноса осей координат.

Рассмотрим кривые второго порядка более подробно.

1. Эллипс:

График симметричен относительно осей координат, полуоси эллипса. Точки и , где называются фокусами эллипса. Число называется эксцентриситетом эллипса (характеризует его «сплюснутость»). Точки М эллипса удовлетворяют характеристическому свойству:

2. Гипербола:

.

График симметричен относительно осей координат. Точки и , где называются фокусами гиперболы. Число  эксцентриситет гиперболы. Прямые называются асимптотами гиперболы. Точки гиперболы удовлетворяют характеристическому свойству

.

3. Парабола:

График симметричен относительно оси .

Точка называется фокусом параболы. Прямая называется директрисой параболы. Считают, что для параболы .

Точки параболы удовлетворяют характеристическому свойству: расстояние от точки до директрисы равно . Общим свойством кривых второго порядка является то, что любую из них можно получить в сечении конуса плоскостью. Поэтому кривые второго порядка называют коническими сечениями.

П р и м е р. Привести к каноническому виду уравнение кривой

.

Р е ш е н и е. В примере п. 2.35.1 квадратичная форма приведена к каноническому виду

в базисе из собственных векторов матрицы квадратичной формы. Найдены собственные значения: ( данная кривая является гиперболой). Имея координаты новых базисных векторов , запишем матрицу преобразования старого базиса в новый. Ее строками являются координаты новых базисных векторов

1 Ж.Б. Фурье (1768-1817) – французский математик.

2 гипер - (от hyper - греч.) – над, сверх.

3 Множество точек в пространстве называется выпуклым, если оно содержит вместе с любой своей парой точек весь отрезок, их соединяющий.

4 additivus – придаточный (лат.).

5 Поскольку далее речь пойдет только о линейных операторах, термин «линейный» будем опускать.

6 homothetas – одинаково расположенный (греч.).

7 сontragradiens - шагающий против (лат.)

108