24. Линейные операторы

Пусть заданы два множества X и Y и указан закон, ставящий в соответствие всякому элементу единственный элемент . Этот закон называется отображением множества X в множество Y. Отображение обозначается или , где А  символ отображения.

Оператор, функция, преобразование – синонимы термина “отображение”. В силу сложившихся традиций каждый из терминов оказался связанным с определенным разделом математики. В частности, в линейной алгебре отображения обычно называют операторами. Например, , где L и  линейные пространства.

Результат действия оператора А на элемент х называется образом элемента х и обозначается

Элемент х принято называть прообразом элемента y.

Оператор А называется линейным оператором, если выполнены следующие условия:

1. аддитивность⁴

(2.25.1)

2. однородность

(2.25.2)

При из условия (2.25.2) следует, что линейный оператор переводит нулевой вектор пространства L в нулевой вектор пространства .

Кроме того, с помощью (2.25.1), (2.25.2) нетрудно видеть, что результат действия линейного оператора на линейную комбинацию произвольных векторов есть линейная комбинация образов этих векторов с теми же коэффициентами т.е.

(2.25.3)

Заметим, что в случае, когда определение линейного оператора соответствует понятию числовой функции одной переменной вида Следовательно, введение понятия оператора позволяет обобщить идею простейшей функциональной зависимости на самые различные множества элементов (например, на линейные пространства).

П р и м е р ы

1. Операция умножения вектора на заданное число 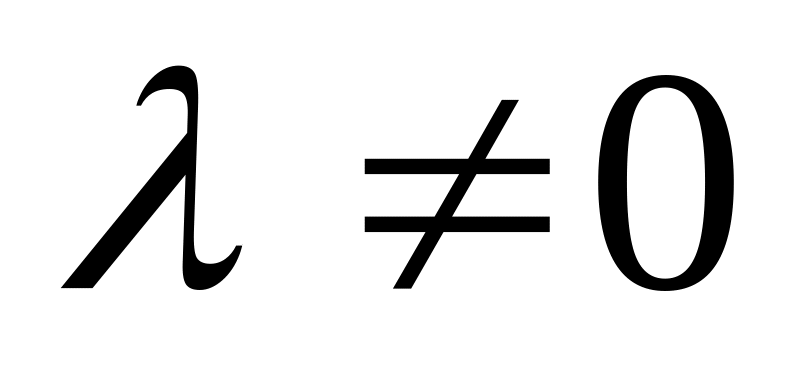есть линейный оператор из L в L , так как

а)

б)

2. Оператор дифференцирования есть линейный оператор из пространства 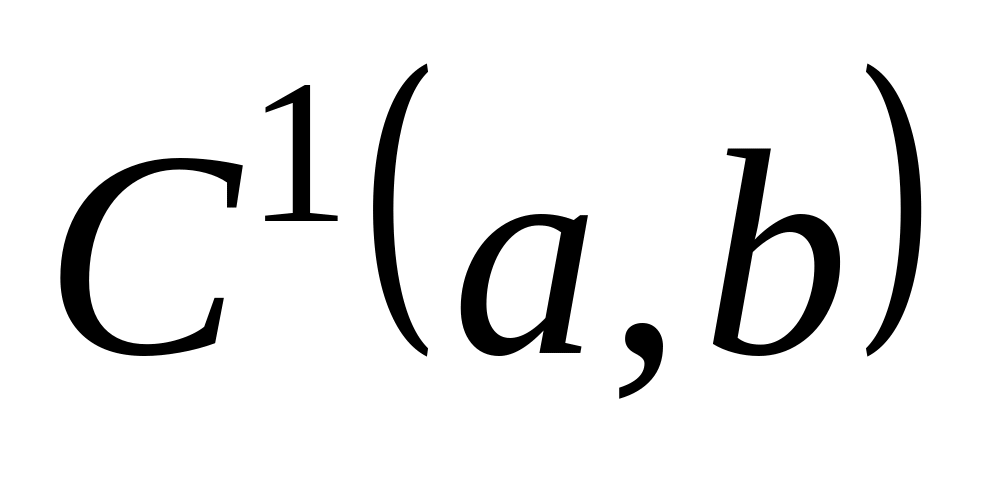в пространство 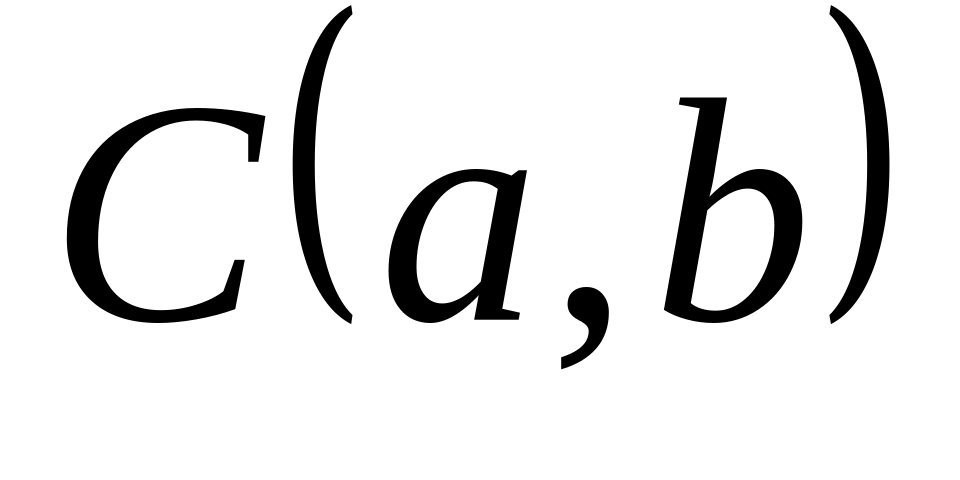, так как

а) ;

б) .

Задание для самостоятельного решения

Установить, какие из заданных отображений пространства в себя являются линейными операторами:

а) где  заданный единичный вектор. Выяснить геометрический смысл этого отображения;

б) и  фиксированы);

в) фиксированный вектор).

2.26. Матрица линейного оператора в заданном базисе

Рассмотрим линейный⁵ оператор .

Пусть и  базис в . Будем считать, что в этом базисе причём

(2.26.1)

Запишем разложения векторов х и у в выбранном базисе

(2.26.2)

и найдем связь между координатами вектора-образа и координатами вектора-прообраза.

Из (2.26.1), (2.26.2) имеем

(2.26.3)

Поскольку то и эти векторы можно разложить в базисе

(2.26.4)

т.е.

Тогда из (2.26.3) (2.26.4) получаем

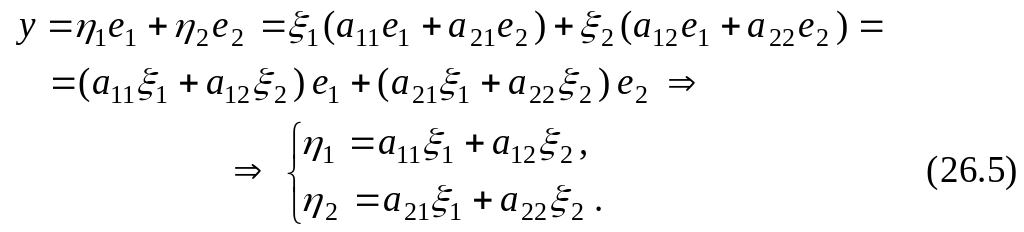
В матричной форме система (2.26.5) равносильна уравнению

(2.26.6)

где (2.26.7)

Таким образом, при наличии базиса результат действия линейного оператора А однозначно определяется матрицей А, которая называется матрицей линейного оператора в заданном базисе.

Столбцами ее служат координаты образов базисных векторов.

Из формулы (2.26.3) ясно, что для задания оператора А достаточно задать лишь образы базисных векторов Тогда образ у любого вектора х будет известен. То же следует из (2.26.6) – (2.26.7).

Рассмотрим теперь оператор

Выберем в пространстве базис и в этом базисе найдем представления координат вектора-образа через координаты вектора . Считая, что и учитывая (2.26.1), нетрудно получить искомые представления

с помощью которых установить, что в заданном базисе квадратная матрица вида

всецело определяет “индивидуальность” линейного оператора Столбцами её, как и в предыдущем случае, служат координаты образов базисных векторов.

Квадратная матрица А п - ного порядка, столбцами которой служат координаты образов базисных векторов, является матрицей линейного оператора в заданном базисе.

Если а то введя в и соответственно базисы и , можно получить формулу вида (2.26.6) и для этого случая. При этом А будет матрицей, а X и Y  матрицами-столбцами, состоящими из п и т элементов соответственно.

Задание для самостоятельного решения

1. Выписать матрицы следующих операторов в ортонормированном базисе пространства :

а)

б) заданный единичный вектор;

в) если

2. Выписать матрицы операторов, действующих в трёхмерном пространстве с ортонормированным базисом:

а)

б)

2.27. НУЛЕВОЙ, ТОЖДЕСТВЕННЫЙ, ПРОЕКТИВНЫЙ

И ГОМОТЕТИЧНЫЙ ОПЕРАТОРЫ

Рассмотрим линейный оператор , где L – линейное п - мерное пространство.

1. Нулевой оператор (О)

Оператор, переводящий любой элемент линейного пространства в нулевой элемент, называется нулевым оператором:

(2.27.1)

Равенство (2.27.1) выполняется лишь в том случае, если в любом базисе координаты векторов будут нулями (это утверждение докажите самостоятельно). Поэтому матрица О оператора О будет нулевой

2. Тождественный оператор (Е)

Оператор, переводящий любой элемент линейного пространства в себя, называется тождественным оператором:

(2.27.2)

Равенство (27.2) будет иметь место только тогда, когда в результате применения оператора система базисных векторов преобразуется в себя, т.е. когда (это утверждение докажите самостоятельно). Очевидно, матрица Е оператора Е в любом базисе будет единичной, т.е.

(2.27.3)