3. Оператор проектирования (р)

Если для любого вектора образ

(2.27.4)

то оператор Р называют оператором проектирования.

При этом вектор п - мерного пространства проектируется на т - мерное подпространство этого пространства. Введенное определение обобщает известное геометрическое представление о проектировании в пространствах и .

Очевидно, что (2.27.4) имеет место только в том случае, когда при и при (проверьте самостоятельно). Поэтому матрица оператора проектирования имеет вид

m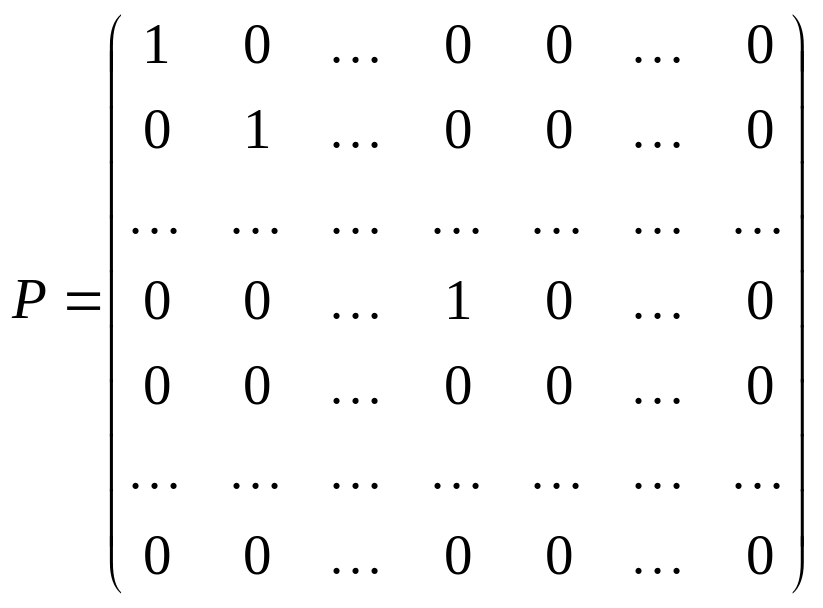

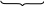
( в базисе ).

4. Оператор гомотетии6 (н)

Если для любого вектора имеет место равенство

(2.27.5)

то оператор Н называется оператором гомотетии (подобия) (рис. 2.18). Поскольку равенство (2.27.5) имеет место лишь при то матрицей оператора гомотетии будет

Задание для самостоятельного решения

1. Доказать, что оператор проектирования обладает следующим свойством: где

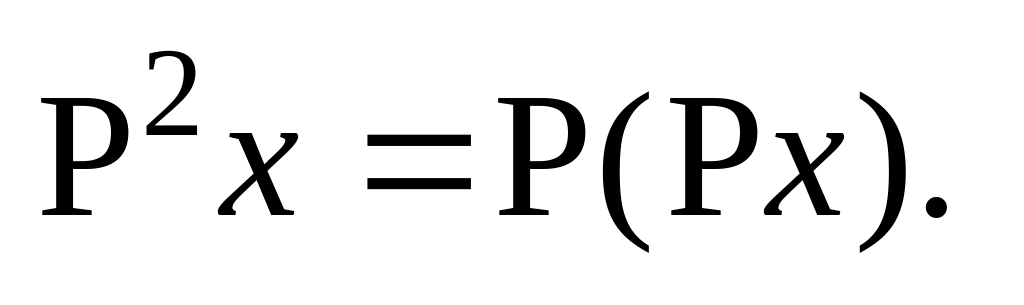
2. Выяснить геометрический смысл оператора 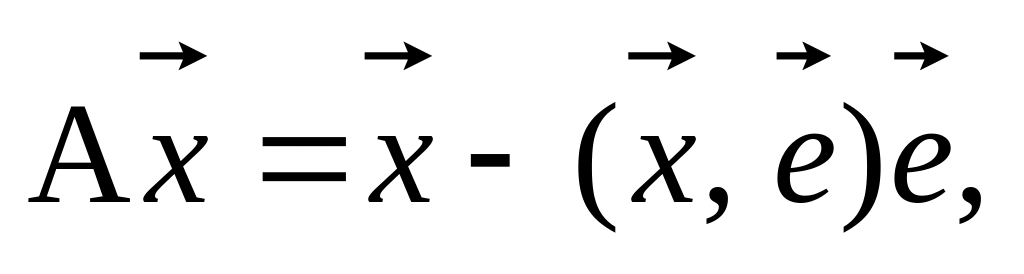где  фиксированный единичный вектор.

2.28. Геометрический смысл матрицы линейного оператора

Рассмотрим оператор Он осуществляет отображение В силу линейности оператора А параллелограмм, постро –

енный на векторах перейдет в параллелограмм, построенный на векторах

Обозначим матрица оператора А в базисе . Тогда, как известно, и

Поскольку площади параллелограммов определяются соответственно формулами

то, вычисляя непосредственно векторные произведения, получим

Следовательно,

т.е. модуль определителя матрицы А является коэффициентом искажения площади в (рис. 2.19).

Если то можно доказать, что

2.29. Действия с операторами

Рассмотрим два оператора А и В, действующие из L в L, где L – линейное пространство.

Над такими операторами вводятся следующие действия:

а) сложение операторов;

б) умножение оператора на число;

в) умножение оператора на оператор.

Приведем определения и рассмотрим свойства каждой из этих операций.

Операторы А и В будем считать равными, если для любого вектора справедливо равенство

(2.29.1)

1. Сложение операторов

Суммой операторов А и В называется оператор , определяемый равенством

. (2.29.2)

Оператор является линейным. Действительно, из (2.29.2),(2.25.2) имеем

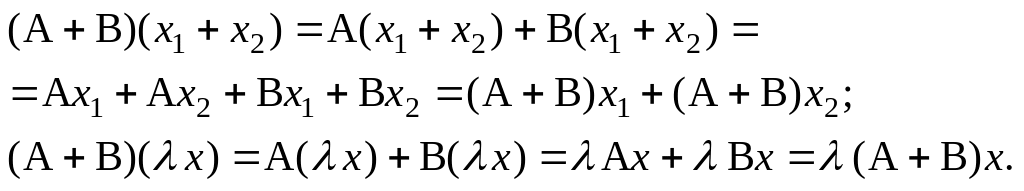
Для n-мерного линейного пространства матрица суммы линейных операторов равна сумме матриц слагаемых (это утверждение докажите самостоятельно).

2. Умножение оператора на число

Отображение, полученное в результате применения к вектору сначала оператора , а затем умножения полученного вектора на число , называется произведением числа на оператор и обозначается через А:

(2.29.3)

Нетрудно видеть, что – линейный оператор. Действительно, учитывая (25.1), (25.2) и (29.3), получаем

Для n-мерного пространства матрица оператора равна произведению числа на матрицу оператора (докажите самостоятельно).

Нетрудно проверить, что введенные операции над линейными операторами обладают свойствами:

1)

2. ;

3. ;

4. ;

5. 

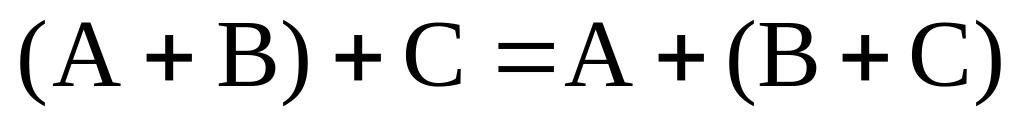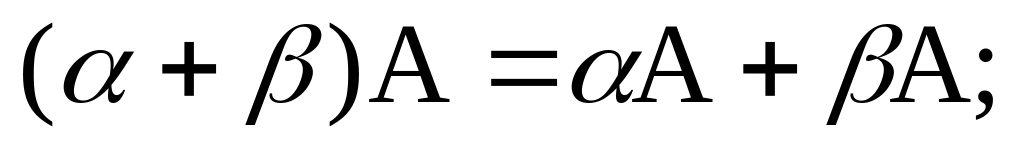
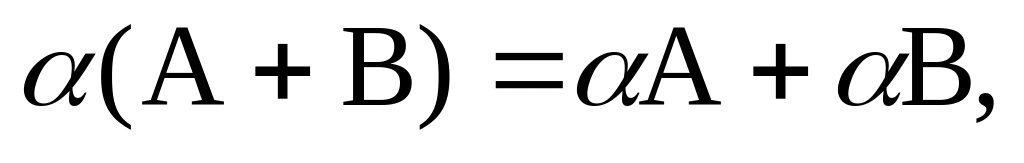6. (2.29.4)

где ,

Равенства (2.29.4) полностью соответствуют аксиомам линейного пространства, приведенным в п. 2.18. Поэтому множество всех линейных операторов, действующих из в , есть линейное пространство.