Задание для самостоятельного решения

1. Для n-мерного евклидова пространства доказать, что 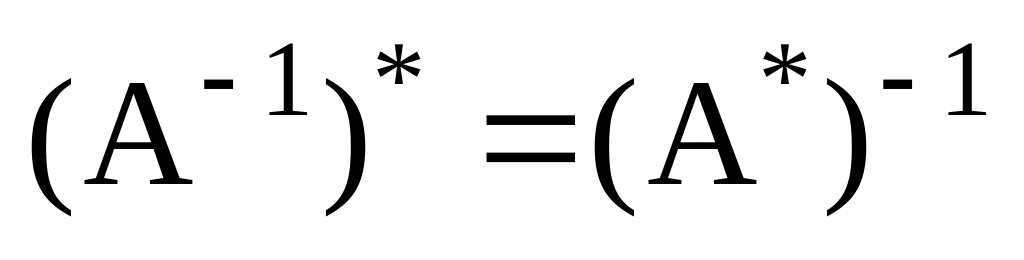, если Аобратимый оператор.

2. Выписать матрицу оператора , если матрица оператора А имеет вид

а) 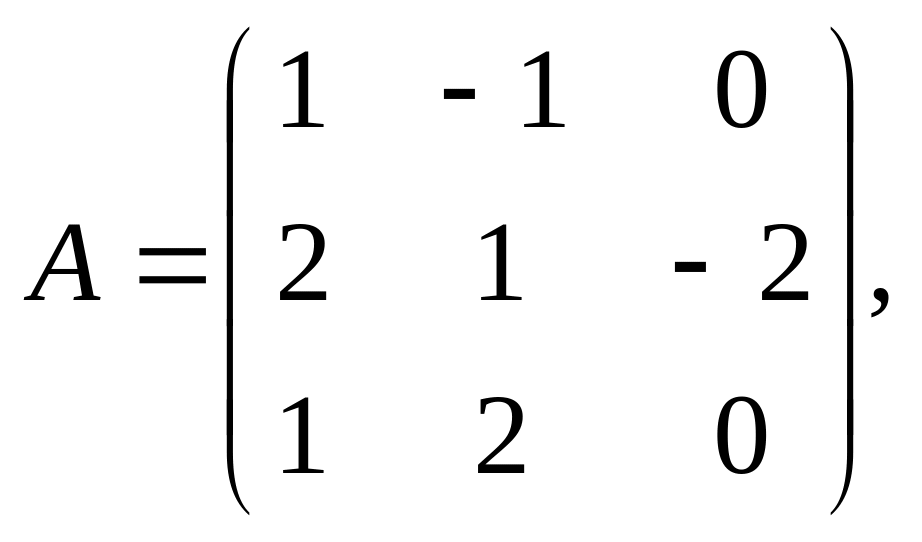б)

3. Для n-мерного евклидова пространства доказать, что

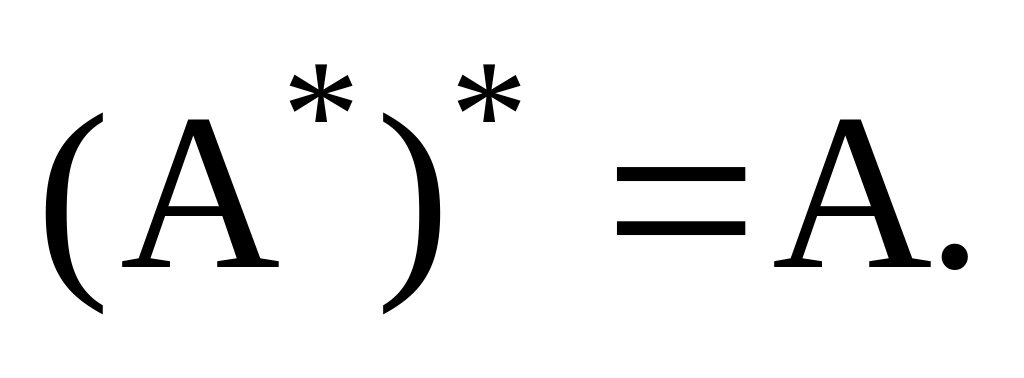
2.31. Самосопряженные операторы. Симметричные матрицы

Если оператор А совпадает с сопряженным оператором, то его называют самосопряженным оператором. В этом случае

(2.31.1)

Самосопряженные операторы обладают следующими свойствами.

1. Сумма самосопряженных операторов и произведение самосопряжен –

ного оператора на действительное число являются также самосопряжен –

ными операторами.

2. Произведение двух самосопряженных операторов является самосопряженным оператором тогда и только тогда, когда эти операторы перестановочны (т.е. когда ).

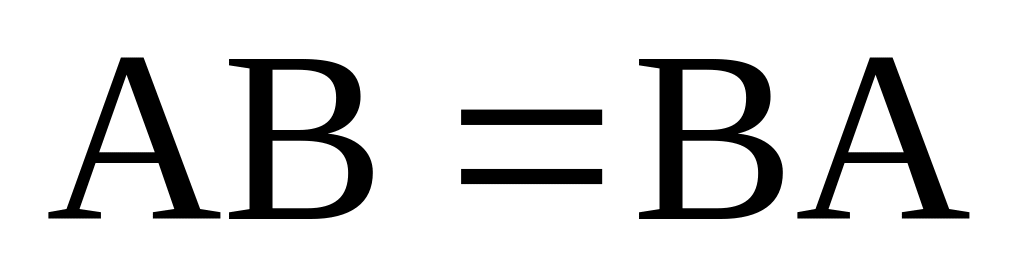Докажем лишь второе из приведенных утверждений.

Итак, пусть операторы А и В перестановочны и таковы, что , . Тогда, учитывая (2.30.2), получим

т. е. АВсамосопряженный оператор.

Наоборот, пусть теперь . Легко видеть, что в этом случае

т. е. операторы перестановочны.

Используя теорему, приведенную в предыдущем пункте, нетрудно доказать еще одно свойство самосопряженных операторов.

3. Для того, чтобы оператор А в n-мерном пространстве был самосопряженным, необходимо и достаточно, чтобы в ортонормированном базисе его матрица была симметричной (т.е. такой, что 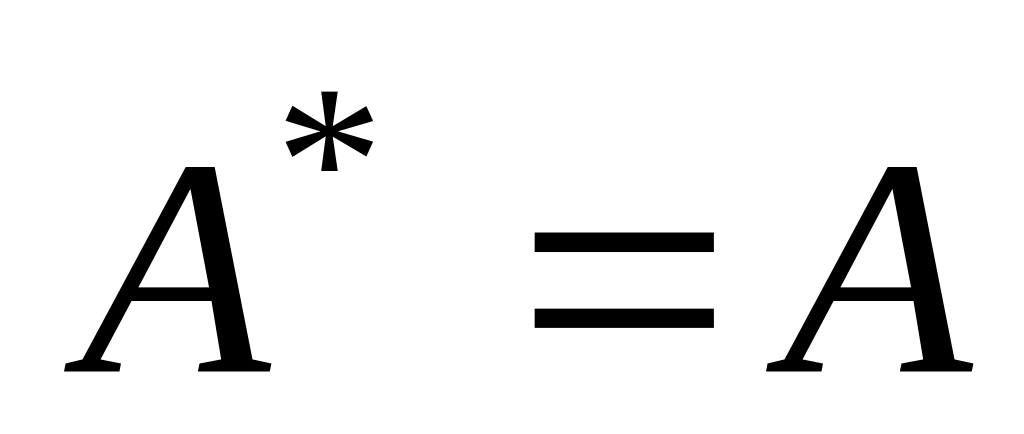). Докажите это утверждение самостоятельно.

В качестве упражнения докажите, что сумма самосопряженных операторов и произведение самосопряженного оператора на действительное число есть самосопряженный оператор (для случая n-мерного евклидова пространства).

2.32. Собственные значения и собственные векторы линейного оператора

Рассмотрим линейный оператор А: .

Под действием этого оператора каждый вектор изменяется вполне определенным образом. Особый интерес представляет собою случай, когда некоторый вектор преобразуется в коллинеарный ему , т.е. когда

(2.32.1)

Вектор х называют тогда собственным вектором, а число , при котором имеет место равенство (2.32.1) - собственным значением оператора А.

Найдем ненулевые решения уравнения (2.32.1), считая что . Перепишем для этого уравнение (2.32.1) следующим образом:

В матричной форме последнее уравнение принимает вид

(2.32.2)

где

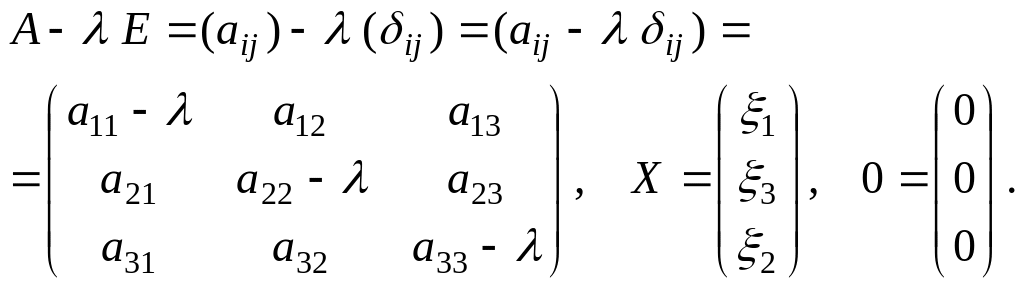
Поэтому имеем

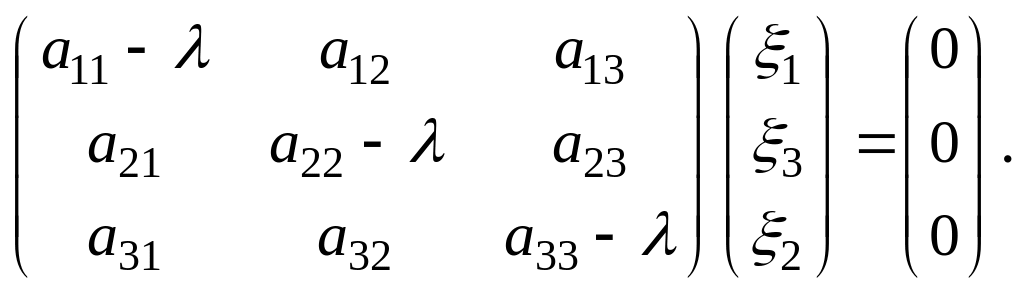(2.32.3)

Матричное уравнение (2.32.3) эквивалентно однородной системе трех линейных алгебраических уравнений

(2.32.4)

с тремя неизвестными и параметром . Ненулевые решения эта система имеет тогда и только тогда, когда ее определитель равен нулю, т.е. когда

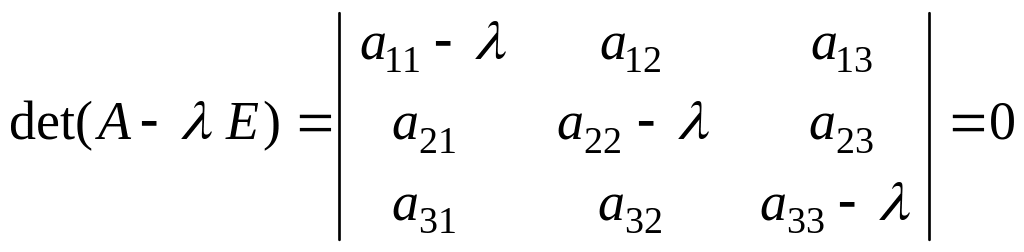. (2.32.5)

Уравнение (2.32.5) называется характеристическим уравнением матрицы и является в данном случае уравнением третьей степени относительно . Оно, как известно, может иметь не более трех действительных различных корней.

Для каждого из этих корней можно составить систему вида (2.32.4) и найти собственный вектор с точностью до скалярного множителя.

Если пространство является n-мерным, то уравнение (2.32.1) также эквивалентно матричному уравнению (2.32.2), в котором

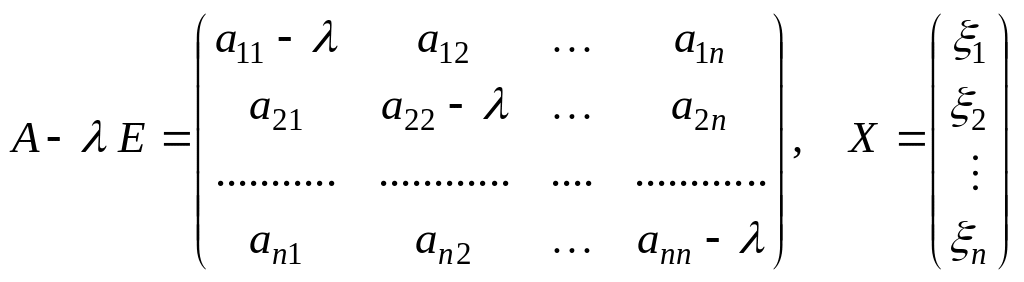(2.32.6)

Поэтому координаты вектора являются решениями однородной системы линейных алгебраических уравнений вида

(2.32.7)

которая имеет ненулевые решения лишь при условии

. (2.32.8)

Уравнение (2.32.8) является характеристическим уравнением для матрицы и может иметь не более действительных различных корней , которые являются собственными значениями оператора А.

Аналогично рассмотренному случаю находят собственные векторы оператора А: , отвечающие различным собственным значениям .

Еще раз подчеркнем, что собственные векторы для каждого собственного значения определяются не единственным образом, а лишь с точностью до скалярного множителя.

Таким образом, для отыскания собственных значений и собственных векторов оператора А следует:

1. составить и решить характеристическое уравнение;

2. решить соответствующую систему линейных алгебраических уравнений.

Особый интерес представляют собственные векторы и собственные значения самосопряженных операторов в евклидовом пространстве. Рассмотрим этот случай более подробно.

Теорема 1. В евклидовом пространстве собственные векторы самосопря –

женного оператора, отвечающие различным собственным значениям, взаимно ортогональны.

Действительно, пусть и – различные собственные значения оператора А, а и – отвечающие им собственные векторы. Тогда

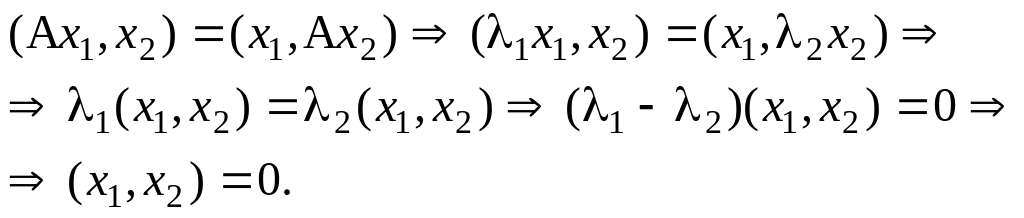
Теорема 2. Для всякого самосопряженного оператора в n-мерном евкли –

довом пространстве существуют взаимно ортогональных собственных векторов.

Эту теорему примем без доказательства. Из нее следует, что собственные векторы самосопряженного оператора образуют ортогональный базис.

Теорема 3. Всякий самосопряженный оператор в n-мерном евклидовом пространстве имеет в базисе из собственных векторов матрицу диагонального вида, причем на главной диагонали ее стоят собственные значения оператора.

Для доказательства рассмотрим самосопряженный оператор с матрицей

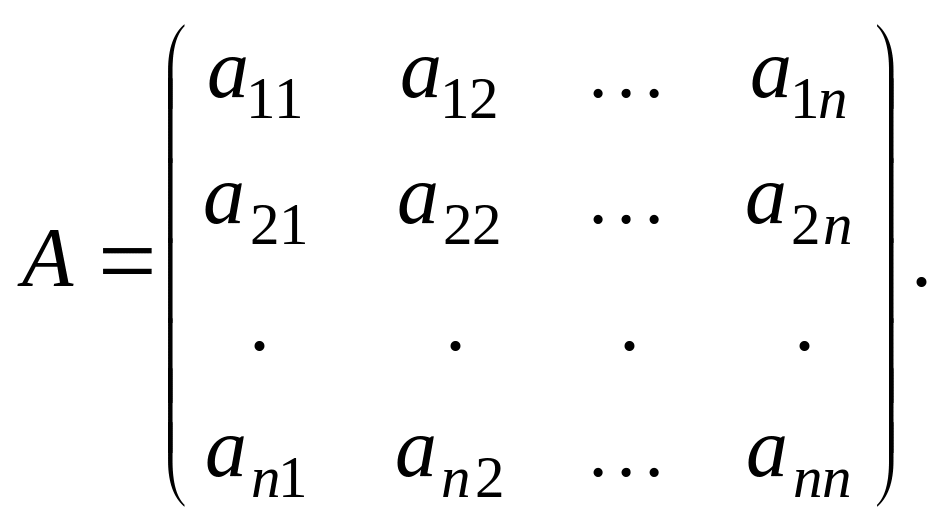
Собственные векторы такого оператора, отвечающие различным собственным значениям попарно ортогональны. Примем их за базис, который обозначим через

Поскольку - собственные векторы, то

Обозначим образы базисных векторов через .

Тогда из предыдущих равенств находим

Напомним, что элементы столбцов матрицы оператора совпадают с координатами образов базисных векторов. Поэтому матрица оператора А в базисе из собственных векторов будет иметь следующий вид:

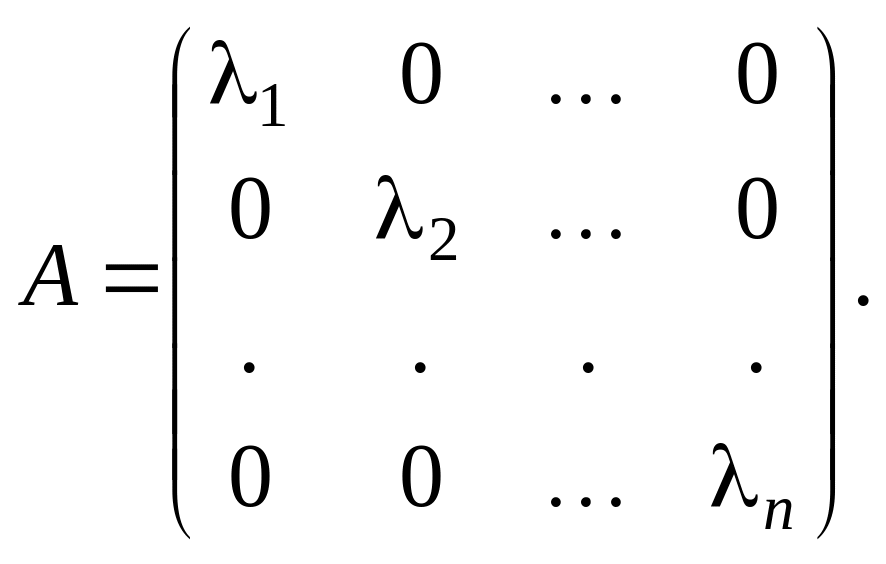
П р и м е р

Найти собственные значения и собственные векторы оператора, матрица которого имеет вид

Записать эту матрицу в базисе из собственных векторов.

1. Составим и решим характеристическое уравнение

2. Составим соответствующую систему линейных уравнений, из которой найдем собственные векторы оператора

Положив , получим

откуда . Считая , найдем собственный вектор .

Положив , получим

т.е. . Считая , найдем второй собственный вектор

Если векторы и нормировать, то получим ортонормированный базис

И з теоремы 3 следует, что в базисе из собственных векторов матрица оператора А примет простейшую (диагональную) форму

Очевидно, что оператор А осуществляет гомотетическое преобразование (рис.2.20).