3. Произведение операторов

Отображение, полученное в результате применения к вектору сначала оператора В, а затем А, называют произведением (композицией) операторов А и В:

(2.29.5)

Порядок сомножителей в произведении операторов существенен, так как, вообще говоря, .

линейный оператор (доказательство этого свойства проведите самостоятельно). Если является n-мерным пространством, то матрица произведения двух линейных операторов равна произведению матриц этих операторов, взятых в том же порядке (мы не доказываем это утверждение).

Композиция операторов подчиняется следующим законам:

1. 

2. 

3. 

4. 

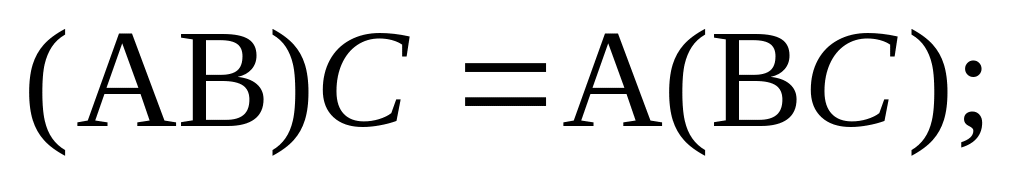
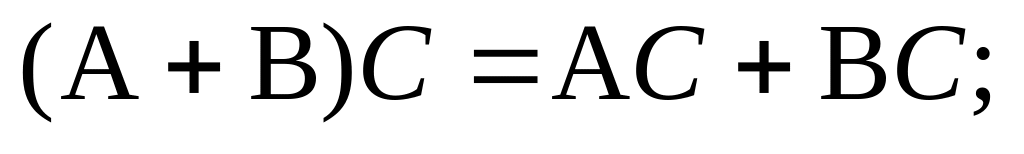
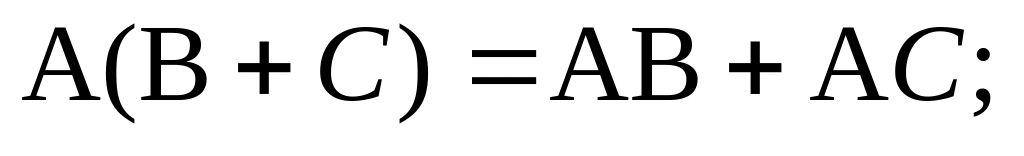
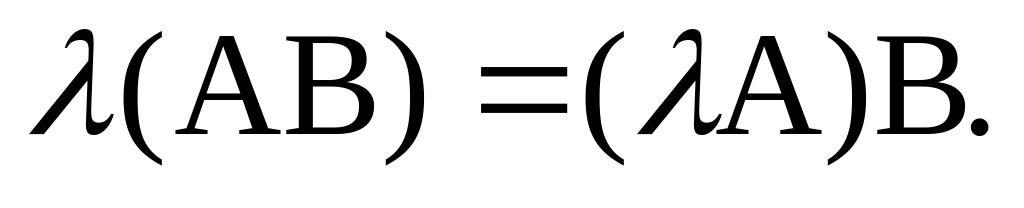5. (2.29.6)

В формулах (2.29.6) через обозначен линейный оператор, через  действительное число.

4. Обратный оператор

Если для линейного оператора существует такой оператор , что

(2.29.7)

то оператор называют обратным оператором по отношению к А, а сам оператор А называется обратимым.

Имеет место следующее утверждение.

Теорема. Любой обратимый оператор имеет только один обратный оператор.

Докажем теорему методом от противного.

Предположим, что обратимый оператор А имеет два обратных оператора и . Тогда, учитывая (2.29.6) и (2.29.7), получим

Оператор линейный (докажите это самостоятельно).

В конечномерном пространстве матрица оператора есть матрица, обратная к матрице оператора А, причем (почему?).

Заметим, что оператор А обратим тогда и только тогда, когда существует взаимно однозначное отображение пространства на себя. Если при этом , то .

Задание для самостоятельного решения

1. В пространстве 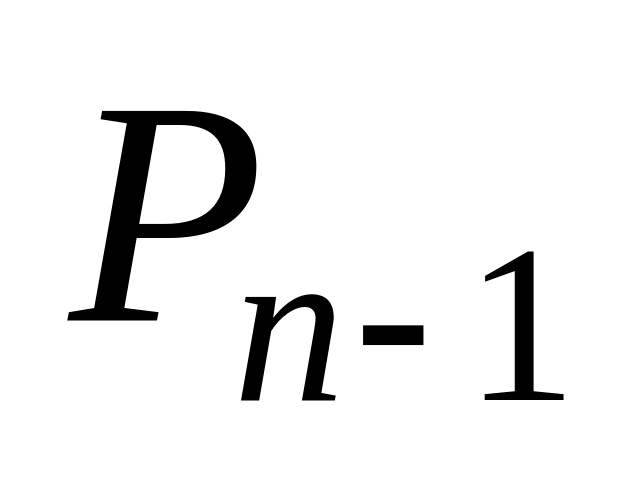многочленов степени не выше 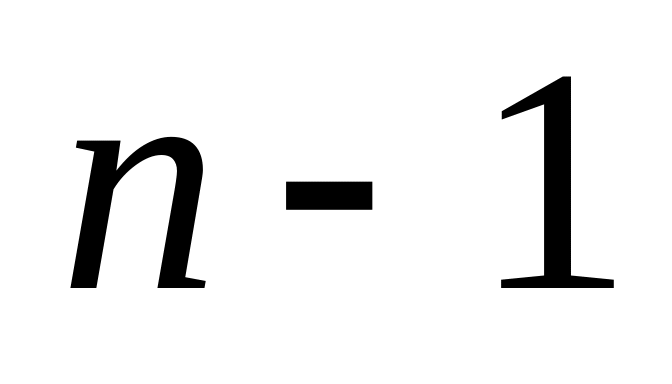задан линейный оператор дифференцирования 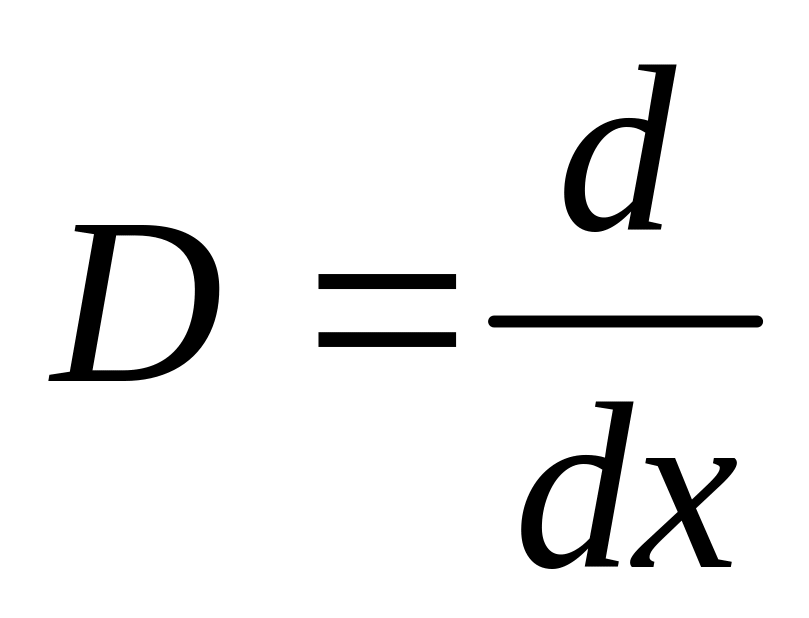. Доказать операторное равенство 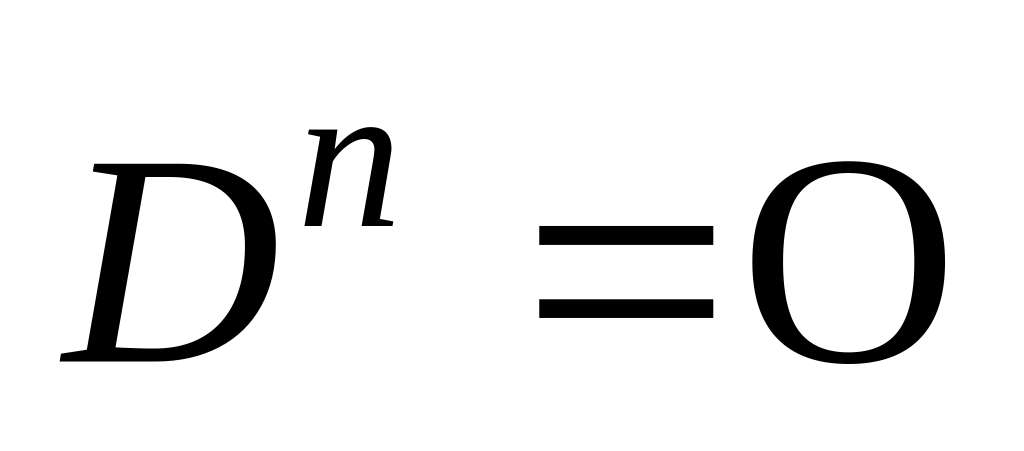(О  нулевой оператор).

2. Доказать, что .

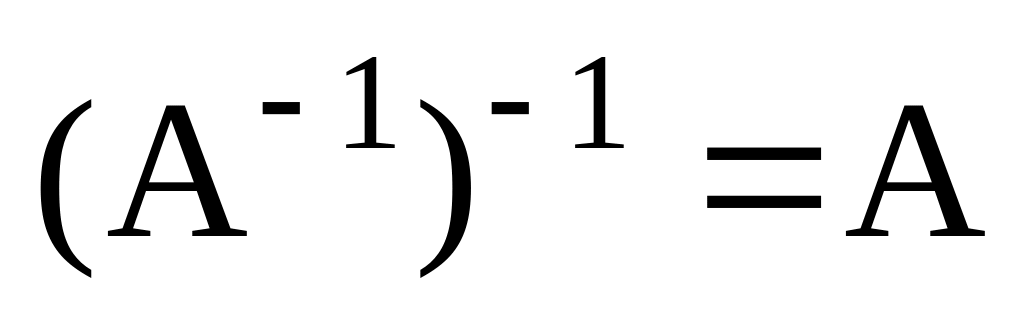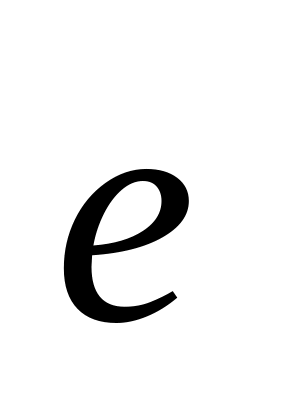
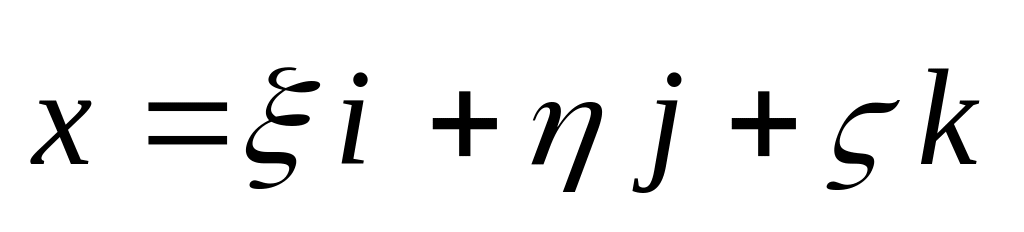3. Установить, какие из заданных операторов являются обратимыми и найти для них явный вид обратных операторов (  фиксированный единичный вектор, ,  фиксированное число):

а) ;

б) ;

в)

г)

д)

2.30. Сопряженный оператор. Сопряженная матрица

Пусть А и – линейные операторы, отображающие евклидово пространство в себя. Операторы А и называют сопряженными, если для любых двух векторов х, y имеет место равенство

(2.30.1)

Можно доказать, что для всякого оператора А сопряженный оператор существует и единственен, а также имеют место следующие свойства:

1)

2)

3)

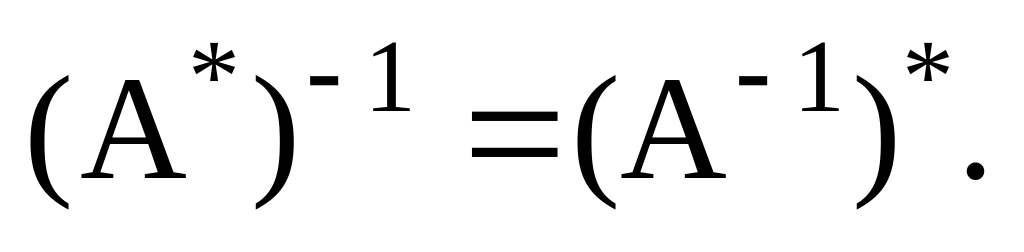4. (2.30.2)

Выясним, как связаны матрицы сопряженных операторов в n-мерном евклидовом пространстве.

Для этого выберем в евклидовом пространстве ортонормированный базис и будем считать, что

(2.30.3)

разложения векторов и по этому базису, т. е. матрица оператора А, а матрица оператора в этом базисе (см.п. (2.26)).

Умножая равенство (2.30.3) скалярно на и используя ортонормированность базиса , найдем

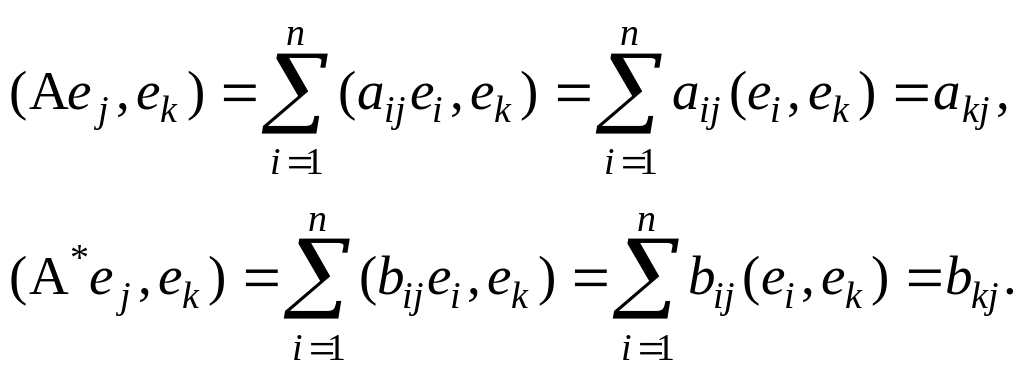
Отсюда согласно (2.30.1) получаем

Следовательно, матрица оператора будет транспонированной матрицей по отношению к матрице .

Полученный результат сформулируем в виде теоремы.

Теорема. Если оператор А в ортонормированном базисе евклидова пространства имеет матрицу , то сопряженный оператор будет иметь в этом же базисе матрицу, равную транспонированной матрице .