
- •2.23. Плоскость и гиперплоскость
- •Прямая линия
- •Линейные операторы
- •2.26. Матрица линейного оператора в заданном базисе
- •Оператор проектирования (р)
- •Оператор гомотетии6 (н)
- •2.28. Геометрический смысл матрицы линейного оператора
- •2.29. Действия с операторами
- •Сложение операторов
- •Умножение оператора на число
- •Произведение операторов
- •Обратный оператор
- •Задание для самостоятельного решения
- •2.30. Сопряженный оператор. Сопряженная матрица
- •Задание для самостоятельного решения
- •2.31. Самосопряженные операторы. Симметричные матрицы
- •2.32. Собственные значения и собственные векторы линейного оператора
- •Задание для самостоятельного решения
- •2.33. Изменение матрицы линейного оператора при преобразовании базиса
- •Задание для самостоятельного решения
- •2.34. Преобразование ортонормированного базиса в ортонормированный
- •2.35. Квадратичные формы
- •2.35.1. Приведение квадратичной формы к каноническому виду
- •Задание для самостоятельного решения
- •2.35.2. Приведение общего уравнения кривых второго порядка к каноническому виду
Задание для самостоятельного решения
Найти собственные значения и собственные векторы оператора проектирования на плоскость Охy в пространстве
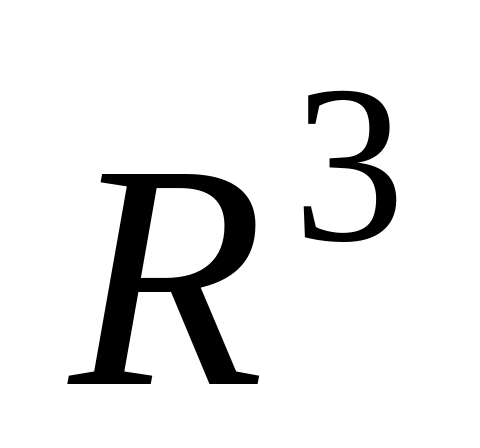 .
.Найти собственные значения и собственные векторы линейного оператора, заданного матрицей:
а)
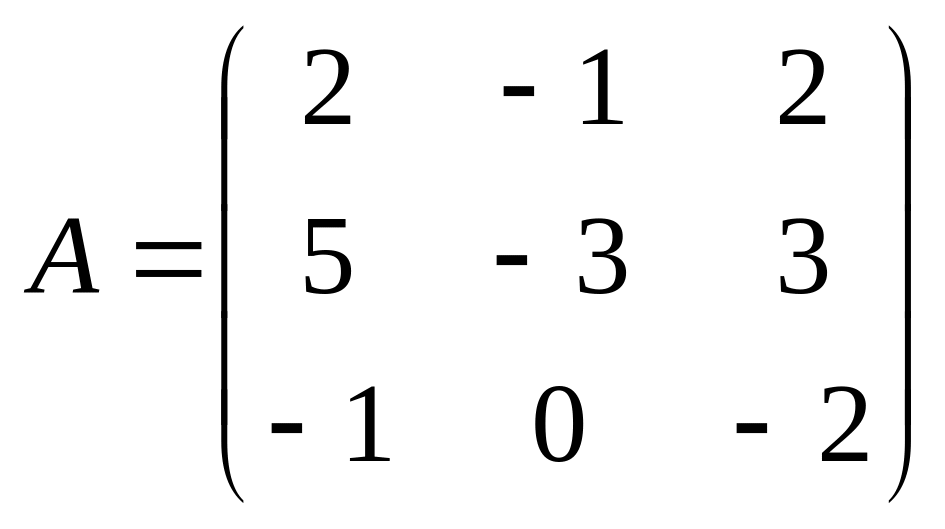 б)
б)
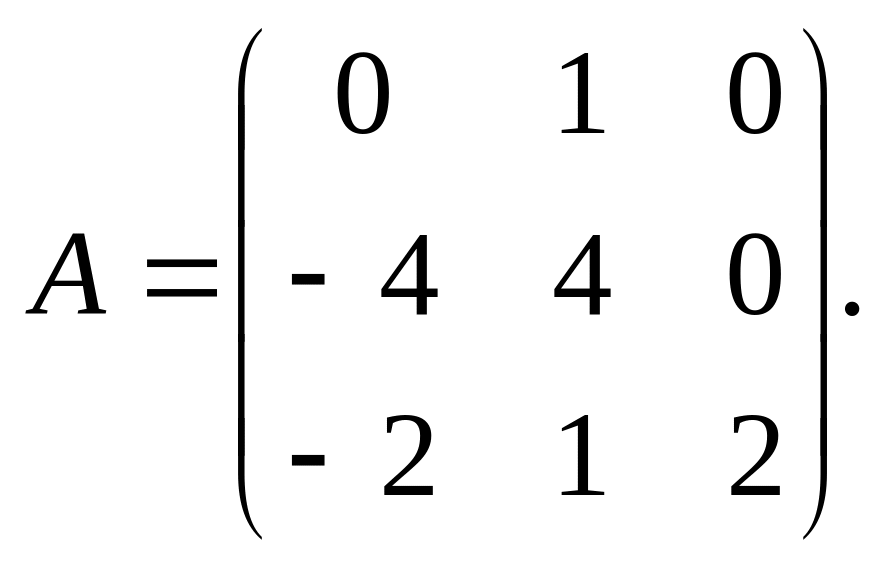
2.33. Изменение матрицы линейного оператора при преобразовании базиса
Как известно, матрица линейного оператора А однозначно определяется совокупностью образов базисных векторов. При изменении базиса матрица оператора также может изменяться. Выясним, как это происходит.
Пусть
![]() некоторый базис в
n-мерном линейном
пространстве
,
а
некоторый базис в
n-мерном линейном
пространстве
,
а
![]() другой базис того
же пространства. Условимся называть
базис
старым, а
новым.
другой базис того
же пространства. Условимся называть
базис
старым, а
новым.
Запишем разложение векторов нового базиса в старом базисе
![]() (2.33.1)
(2.33.1)
Равенства (2.33.1) можно записать в матричной форме
![]()
где
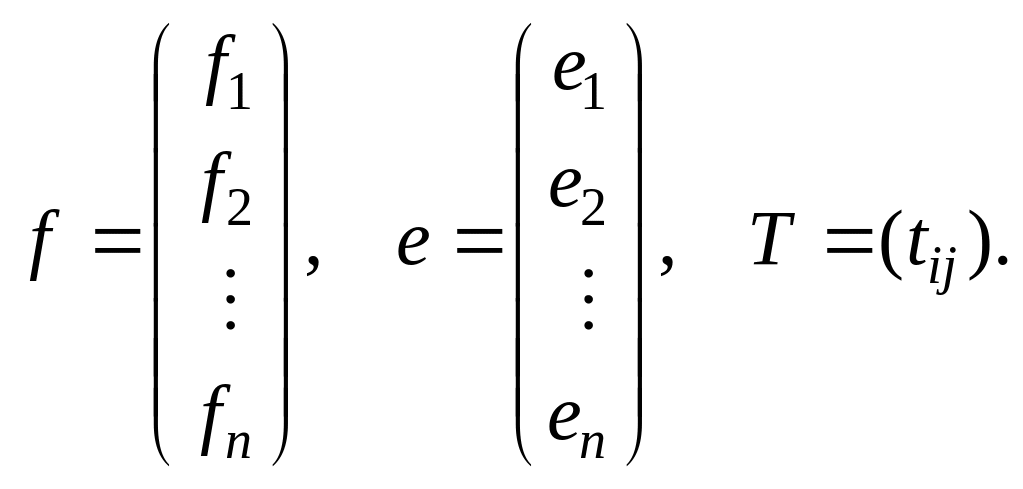 (2.33.2)
(2.33.2)
Матрица
![]() является матрицей перехода от старого
базиса к новому, причем,
является матрицей перехода от старого
базиса к новому, причем,
![]() ,
поскольку векторы
,
поскольку векторы
![]() должны однозначно выражаться через
должны однозначно выражаться через
![]() .
.
Обозначим координаты одного и того же
вектора
в старом базисе через
![]() ,
а в новом через
,
а в новом через
![]() .
Учитывая разложение
в старом и новом базисах, имеем
.
Учитывая разложение
в старом и новом базисах, имеем
![]() (2.33.2)
(2.33.2)
Используя разложения (2.33.1) в виде
![]() ,
перепишем равенство (2.33.2) следующим
образом:
,
перепишем равенство (2.33.2) следующим
образом:
![]() .
.
Из последнего следует, что
![]()
т.е.
![]() .
(2.33.3)
.
(2.33.3)
В матричной форме соотношение (33.3) принимает вид
![]() ,
(2.33.4)
,
(2.33.4)
где
![]() и
и
![]()
матрицы-столбцы с элементами
и
соответственно.
Из формулы (2.33.4) находим
матрицы-столбцы с элементами
и
соответственно.
Из формулы (2.33.4) находим
![]() (2.33.5)
(2.33.5)
Матрицу
![]() называют контраградиентной7
по отношению к матрице
.
называют контраградиентной7
по отношению к матрице
.
Учитывая полученные формулы преобразования координат вектора при изменении базиса, найдем формулу преобразования матрицы оператора А.
![]() (2.33.6)
(2.33.6)
Таким образом, оператору, имеющему в
старом базисе матрицу
![]() ,
в новом базисе соответствует оператор
с матрицей
,
в новом базисе соответствует оператор
с матрицей
![]() .
Если новый базис (т.е. матрицу
)
выбрать удачно, то в новом базисе матрица
может принять более простой вид (см.
пример из п. 2.32).
.
Если новый базис (т.е. матрицу
)
выбрать удачно, то в новом базисе матрица
может принять более простой вид (см.
пример из п. 2.32).
Задание для самостоятельного решения
Найти матрицу оператора А, заданного в базисе
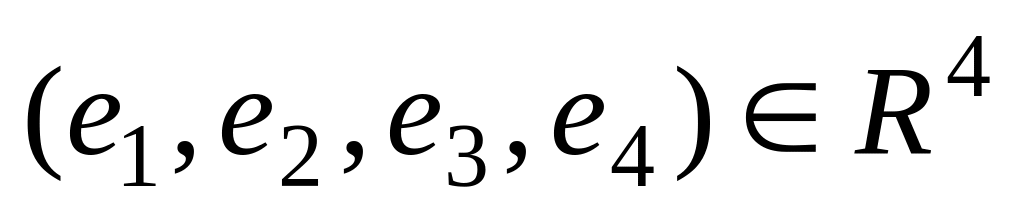 матрицей
матрицей
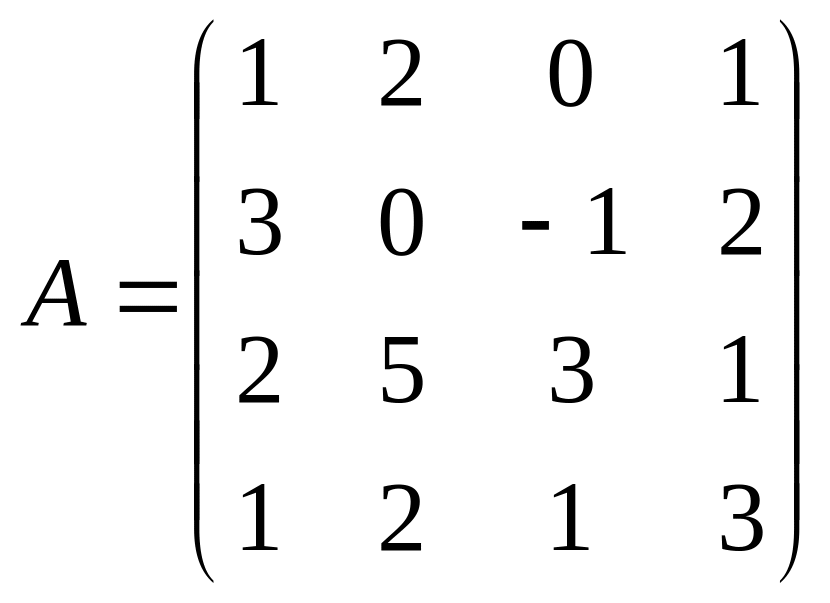
в новом базисе
![]()
В пространстве
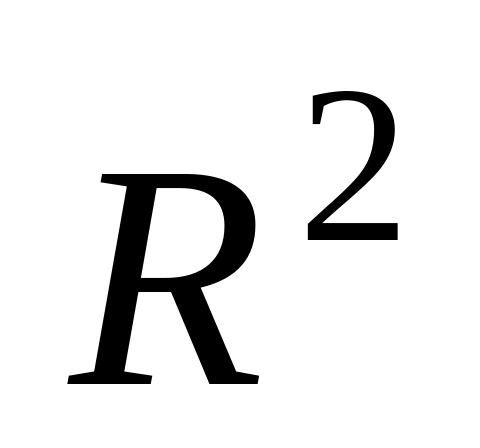 оператор А в базисе
оператор А в базисе
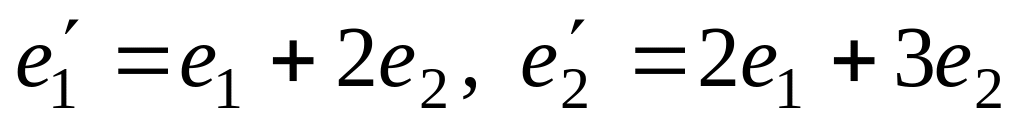 имеет матрицу
имеет матрицу
![]()
Оператор
![]() в базисе
в базисе
![]() имеет матрицу
имеет матрицу
![]()
Найти матрицу
оператора
![]() в базисе
в базисе
![]()
В базисе
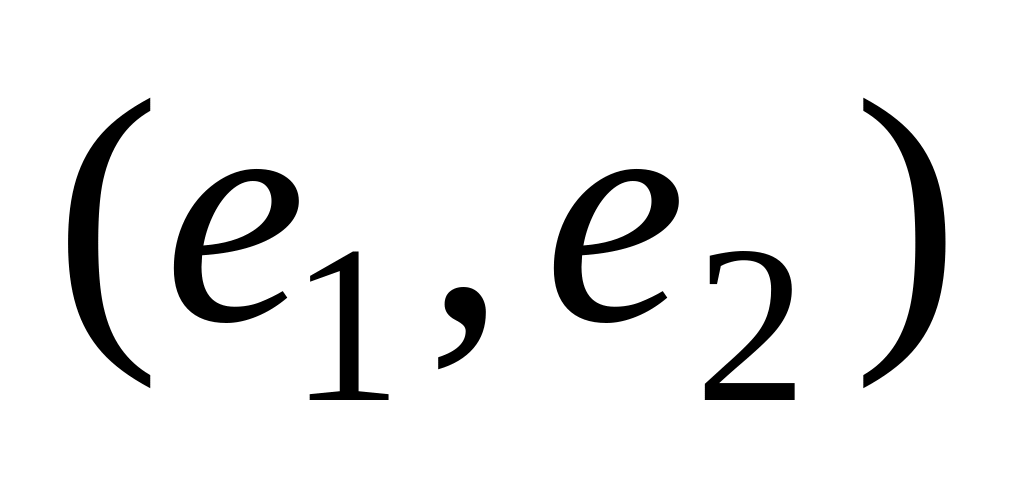 оператор А имеет матрицу
оператор А имеет матрицу
![]() .
.
Записать матрицу этого оператора в новом базисе
![]()
2.34. Преобразование ортонормированного базиса в ортонормированный
Пусть теперь и ортонормированные старый и новый базисы в евклидовом пространстве. Тогда имеем
![]() (2.34.1)
(2.34.1)
Отсюда следует, что
![]()
т.е. матрица обладает свойством ортонормированности по строкам:
![]() .
(2.34.2)
.
(2.34.2)
Очевидно, что
![]() .
(2.34.3)
.
(2.34.3)
Запишем теперь обратное по отношению к (2.34.1) преобразование:
![]() (2.34.4)
(2.34.4)
где
![]() .
.
Очевидно,что
![]() (2.34.5)
(2.34.5)
Сравнивая (2.34.5) с (2.34.3), получим
![]()
т.е.
![]() ,
или
,
или
![]() .
(2.34.6)
.
(2.34.6)
Так как матрица
![]() ортогональна по строкам (см. (2.34.4)), то
матрица
ортогональна
по столбцам. Таким образом, свойство
ортогональности имеет место одновременно
и по строкам, и по столбцам. На этом
основании введем понятие ортогональной
матрицы.
ортогональна по строкам (см. (2.34.4)), то
матрица
ортогональна
по столбцам. Таким образом, свойство
ортогональности имеет место одновременно
и по строкам, и по столбцам. На этом
основании введем понятие ортогональной
матрицы.
Квадратная матрица называется ортогональной, если для ее элементов выполняются условия
![]()
Замечательное свойство ортогональных матриц выражено формулой (2.34.6): обратная матрица для ортогональной матрицы совпадает с транспонированной матрицей.
Другое замечательное свойство ортогональных матриц сформулируем в виде следующей теоремы.
Теорема 1. При преобразовании ортонормированного базиса в ортонор –
мированный скалярные произведения векторов не изменяются.
Для доказательства рассмотрим координаты двух произвольных векторов х и у в старом и новом базисе
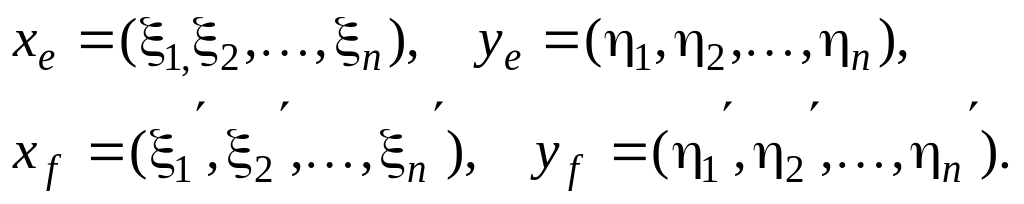
Связь координат вектора в старом и новом
базисе определяется формулой (2.33.5),
которая с учетом (2.34.6) принимает вид
![]() ,
т.е.
,
т.е.
![]() (2.34.7)
(2.34.7)
Отсюда имеем
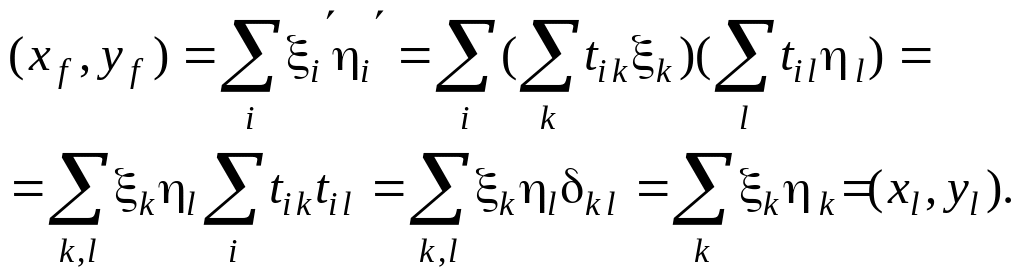
Таким образом, при ортогональном изменении базиса сохраняются модули векторов и углы между ними, т.е. пространство «поворачивается» как одно целое (слово «поворачивается» взято в кавычки, т.к. наряду с обычными поворотами возможны еще преобразования симметрии).
П р и м е р ы
П
 усть
в
ортогональная система координат
поворачивается на угол
усть
в
ортогональная система координат
поворачивается на угол
 (рис.2.21).
(рис.2.21).
Так как согласно (2.34.3)
![]()
то
![]()
![]()
С помощью (2.33.4) запишем выражение координат вектора в старом базисе через его координаты в новом базисе:
![]()
В все выглядит аналогично:
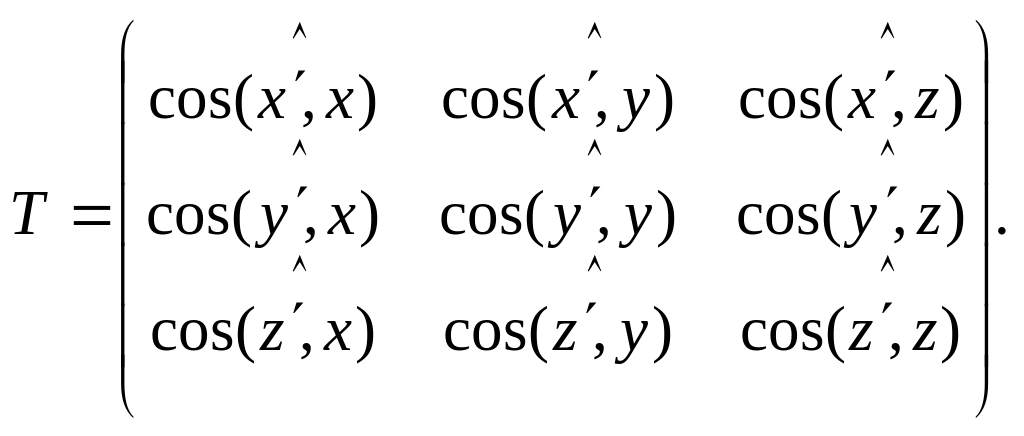
Теорема 2. Если самосопряженному оператору в ортонормированном базисе соответствует матрица , то существует ортогональное изменение базиса с матрицей , приводящее матрицу к диагональному виду:
![]()
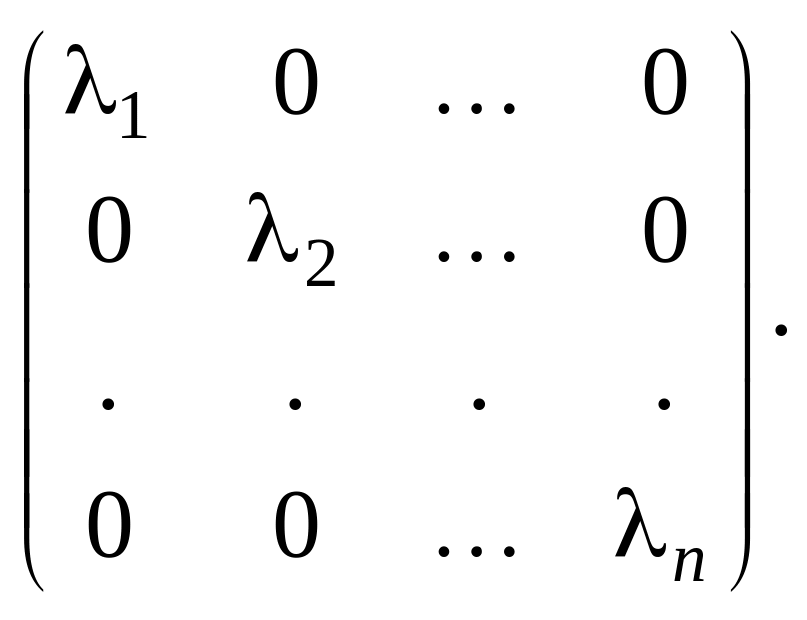
Для доказательства достаточно выбрать
в качестве новых базисных векторов
нормированные собственные векторы
оператора. Тогда матрица Т может
быть построена в соответствии с (2.34.3).
В новом базисе оператор А будет задавать
отображение вектора
![]() на вектор
на вектор
![]() ,
т.е. матрица оператора в новом базисе
будет диагональной.
,
т.е. матрица оператора в новом базисе
будет диагональной.
