5. 2.35. Квадратичные формы

2.35.1. Приведение квадратичной формы к каноническому виду

Квадратичной формой переменных называется однородный многочлен второй степени

(2.35.1)

Из коэффициентов при этом можно образовать матрицу которая называется матрицей квадратичной формы.

При n = 2 из (2.35.1) получаем квадратичную форму двух переменных

Из последней формулы ясно, что, не ограничивая общности, можно считать т.е.

(2.35.2)

Таким образом, матрица квадратичной формы является симметричной.

Если ввести вектор и обозначить через А самосопряженный оператор, отвечающий матрице в ортонормированном базисе , то (35.1) можно записать короче:

(2.35.3)

Равенство (2.35.3) следует из известных соотношений:

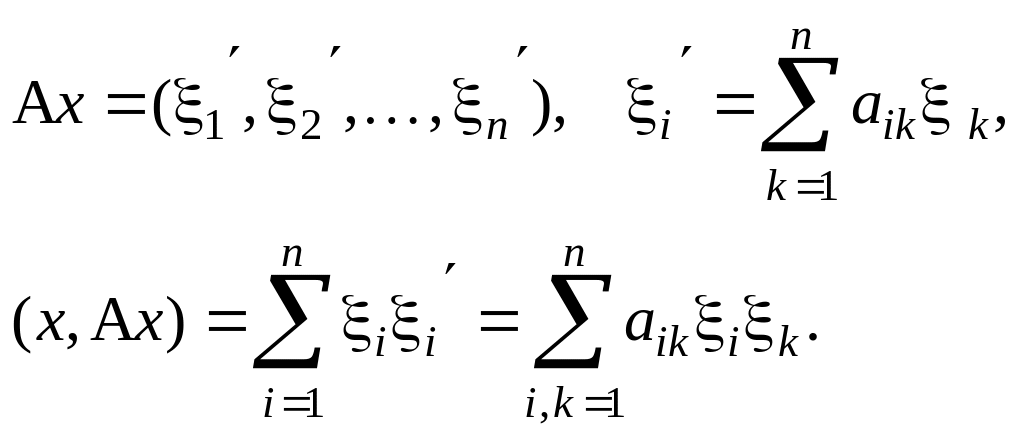
При изменении базиса матрица квадратичной формы тоже изменяется (как матрица линейного оператора). Говорят, что квадратичная форма приведена к каноническому виду, если все при . Это означает, что для приведения квадратичной формы к каноническому виду нужно избавиться от слагаемых, содержащих произведения переменных. Так как оператор А является самосопряженным, он имеет взаимно ортогональных собственных векторов, определяющих новый ортонормированный базис , в котором матрица квадратичной формы принимает диагональный вид.

Совершая переход от старого базиса к новому , мы приведем матрицу к диагональному виду

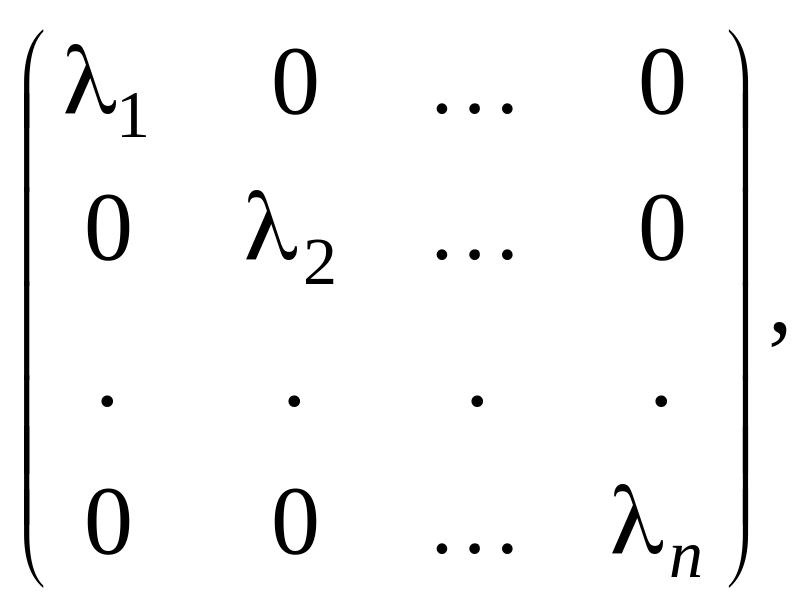(2.35.4)

где  собственные значения матрицы . Тогда вместо (2.35.1) в новой системе координат мы получим более простую формулу. Действительно, вектору в новом базисе будет соответствовать вектор

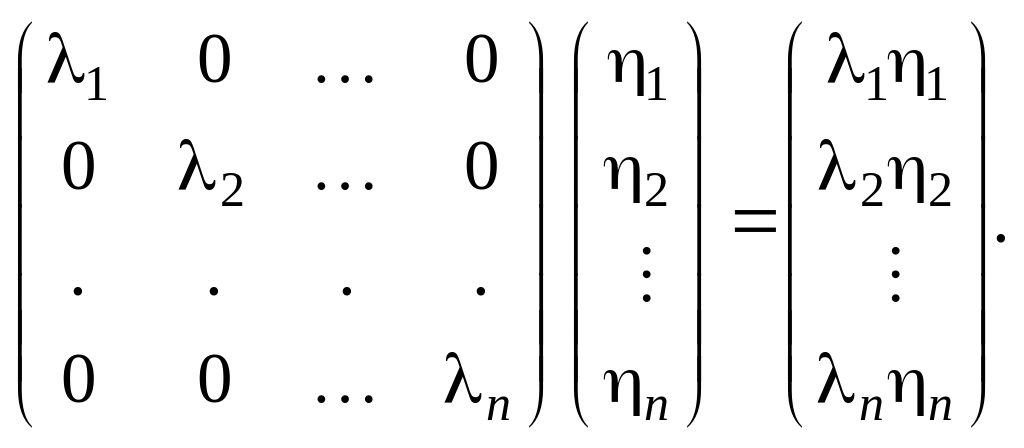
Поэтому в каноническом виде квадратичная форма выглядит следующим образом:

(2.35.5)

где  образ вектора в новом базисе. Коэффициенты при квадратах переменных в (2.35.5) являются собственными значениями матрицы А.

З а м е ч а н и е. На плоскости или в пространстве переход от старого базиса к новому с геометрической точки зрения осуществляется поворотом осей координат так, что новые оси будут направлены по новым базисным векторам.

Для того, чтобы проверить, сохранилась ли ориентация системы координат при переходе к новому базису, вычисляют определитель , столбцами которого являются координаты единичных собственных векторов матрицы . Если , то ориентация сохранилась, если , то ориентацию осей следует изменить.

На основании изложенного процедура приведения квадратичной формы к каноническому виду состоит в следующем:

1. составить матрицу квадратичной формы;

2. составить характеристическое уравнение матрицы ;

3. вычислить собственные значения матрицы А;

4. составить однородную систему уравнений 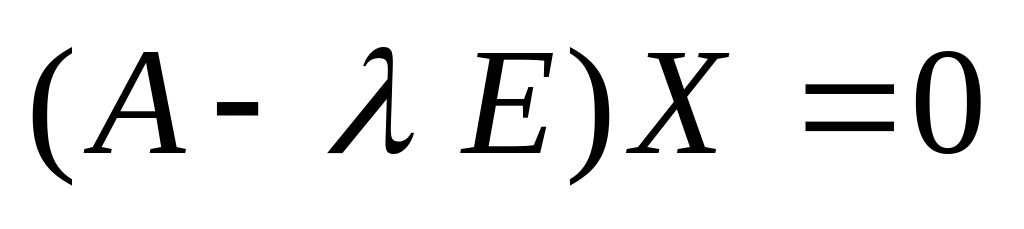и найти собственные векторы матрицы ;

5) образовать новый ортонормированный базис из собственных векторов;

6. записать канонический вид квадратичной формы.

Принята следующая классификация квадратичных форм: если все , то квадратичная форма называется положительно определенной; если все , то  отрицательно определенной; если все или все (но имеется хотя бы одно значение ), то  знакопостоянной; если среди есть и положительные и отрицательные значения, то  знакопеременной.

В качестве примера приведем к каноническому виду квадратичную форму

Р е ш е н и е

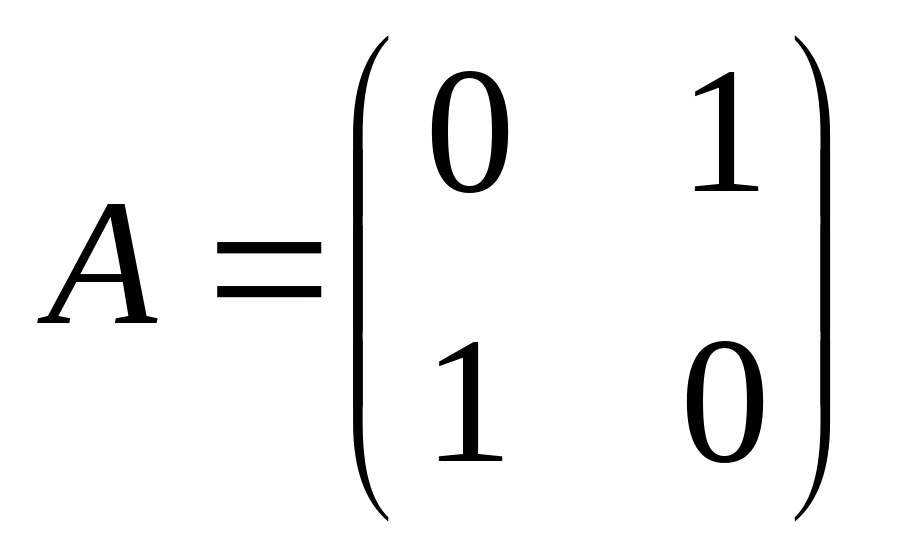1.  матрица квадратичной формы;

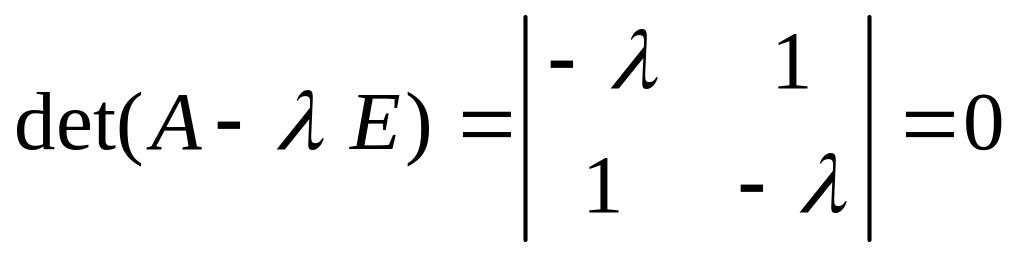2.  характеристическое уравнение;

3.  собственные значения матрицы ;

4. 

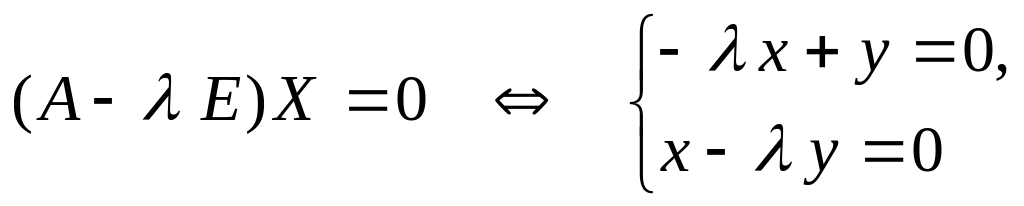
 система для определения координат собственных векторов.

5.  ориентация новой системы 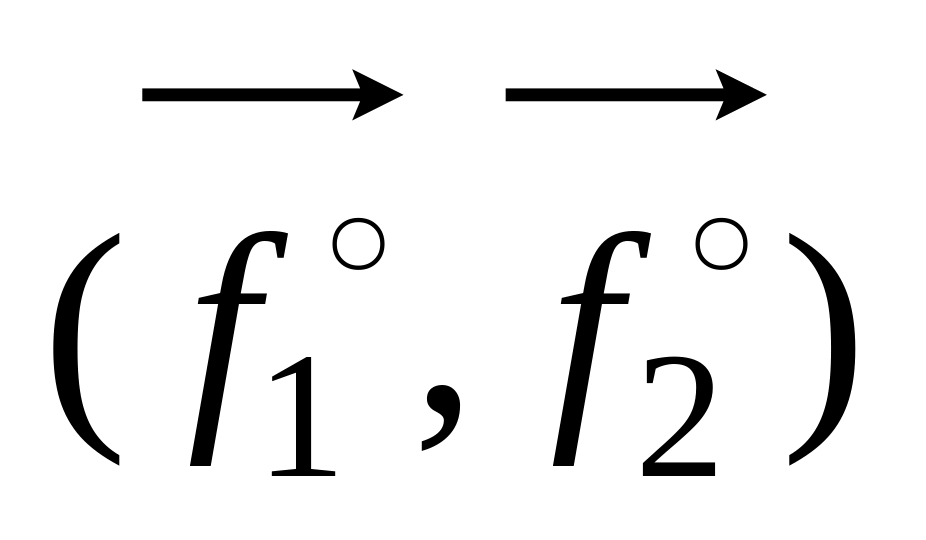верна;

6. в базисе имеем

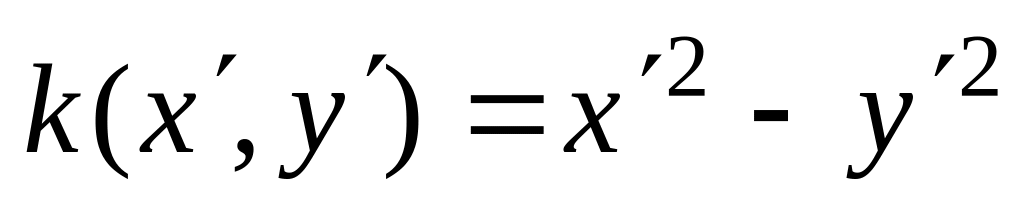
 канонический вид квадратичной формы.

Отметим, что процедура приведения квадратичной формы к каноническому виду используется при исследовании и приведении к каноническому виду общего уравнения второй степени