5.2.Однородные координаты и преобразования в пространстве

Современные системы компьютерной графики работают не только с плоскими изображениями, но и с объемными (трехмерными). Для выполнения преобразований в трех измерениях естественно распространить матричные операции и на трехмерные геометрические объекты. Для этого по аналогии с двухмерным случаем введем понятие однородных координат точки в пространстве. Заменим тройку чисел (x, y, z) четверкой (x, y, z, 1). В общем виде однородные координаты представляются в виде .

Рис. 5.32 – Куб и гиперкуб.

Как представить себе смысл величины h? По аналогии с двухмерным случаем h есть расстояние от координатного пространства XYZ до проективной гиперплоскости, на которую это пространство проектируется. Размерность гиперплоскости равна четырем. Мысленно представить себе четырехмерный объект практически невозможно (Рис. 5 .32). Например, каждой гранью четырехмерного гиперкуба является привычный нам трехмерный куб и т.д.

Зададим элементарные операции в пространстве в виде матриц.

Матрица вращения вокруг оси абсцисс на угол :

Следует помнить, что матрица соответствует линейной системе уравнений координат точек.

Матрица вращения вокруг оси ординат на угол :

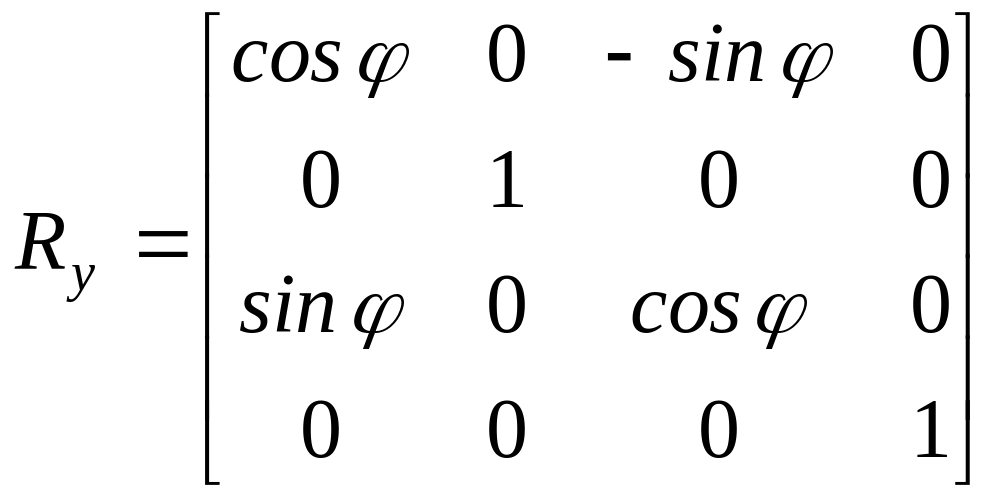
Матрица вращения вокруг оси аппликат на угол :

Очень важное свойство вращения в пространстве состоит в том, что оно некоммутативно. Коммутативностью называется независимость результата операции от порядка следования операндов. Например, для обычных чисел AB=BA. Для матриц же такое правило не соблюдается: при умножении матриц в общем случае ABBA. И действительно, результат вращения тела в пространстве зависит от последовательности выполнения вращений. Отметим, что вращение на плоскости вcегда коммутативно. Мы можем сначала повернуть объект на 15^о, а затем на 30^о, или наоборот – сначала на 30^о, а затем на 15^о – в обоих случаях тело окажется повернутым на 45^о.

Матрица масштабирования с коэффициентами сжатия/растяжения вдоль оси абсцисс, - оси ординат, - оси аппликат:

Для определения переноса объекта удобно воспользоваться вектором переноса с координатами , вдоль которого объект и перемещается в направлении вектора. Тогда можно записать следующую матрицу переноса:

6.Моделирование поверхностей

Системы 3D моделирования должны тем или иным образом математически представлять трехмерные поверхности, из которых образуются моделируемые тела.

Поверхностная модель объекта определяется с помощью точек, линий и поверхностей. Метод поверхностного моделирования наиболее эффективен при проектировании и изготовлении сложных криволинейных поверхностей, таких, как корпуса автомобилей.

Существуют следующие основные типы поверхностей

1. Базовые геометрические поверхности. К ним относятся плоские поверхности, которые можно получить, начертив сначала отрезок прямой, а затем введя такую команду, которая разворачивает в трехмерном пространстве образ этого отрезка на заданное расстояние. Подобным образом (разверткой окружностей или дуг) могут быть сгенерированы цилиндрические и конические поверхности (Рис. 6 .33).

Области поверхностей также могут быть развернуты в трехмерные объекты (Рис. 6 .34). Следует отметить, что системы поверхностного моделирования не распознают такие формы, как твердые объемные тела; они представляют их просто как поверхности (на Рис. 6 .34 семь плоских граней), соединенные друг с другом неким образом в пространстве и ограничивающие "пустой" объем.

Рис. 6.33 – Формирование развернутых плоских и криволинейных поверхностей.

Рис. 6.34 – Формирование объемного объекта разверткой плоской области.

2. Поверхности вращения могут быть легко получены по команде, создающей поверхность вращением плоской грани вокруг определенной оси (эту процедуру можно трактовать как "круговую развертку"). При этом опять необходимо помнить, что создается не объемное тело, а генерируется только поверхность (Рис. 6 .35).

3. Поверхности сопряжении и пересечений. Возможность построения плавного сопряжения одной поверхности с другой является наиболее мощным и часто используемым на практике средством поверхностного моделирования. Кроме этого, может быть доступно средство определения пересечения поверхностей.

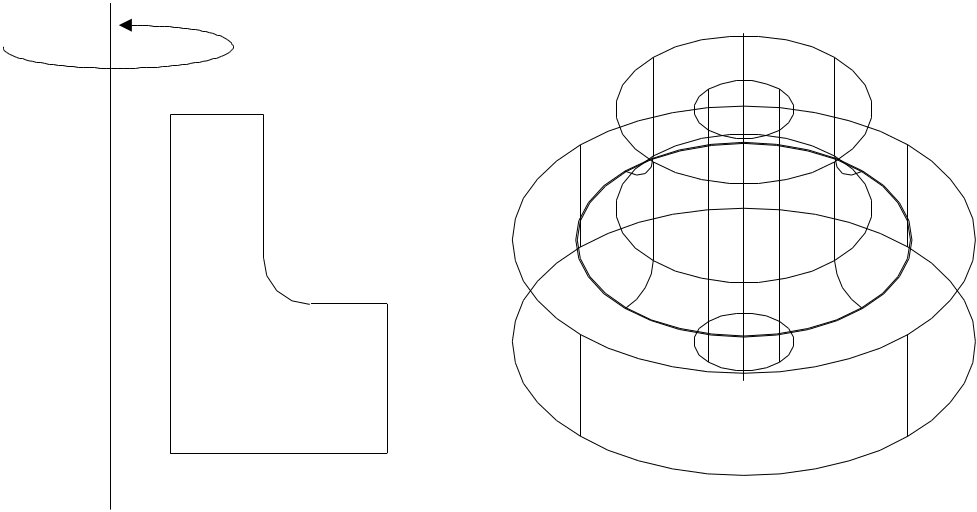
Рис. 6.35 – Получение поверхности вращения.

Рис. 6.36 – Поверхности сопряжения.

На Рис. 6 .36 показано, как в трехмерном пространстве можно построить обычное и плавное сопряжения боковых поверхностей параллелепипеда и цилиндра. Проблема порождения результирующей поверхности в данном случае сводится к задаче построения методом сплайн-интерполяции особых кривых в трехмерном пространстве, "выходящих" из сторон квадрата и "входящих" в автоматически генерируемую кривую на поверхности цилиндра, по которой заданные поверхности должны пересекаться.

4. Аналитические поверхности. Каждая такая поверхность определяется одним математическим уравнением с неизвестными X, Y и Z (эти неизвестные обозначают искомые координаты поверхности). Иначе говоря, чтобы изобразить любую аналитическую поверхность, необходимо знать математическое уравнение, которым она описывается. На Рис. 6 .37 представлена поверхность, описываемая уравнением .

Рис. 6.37 – Аналитически заданная поверхность.

Аналитические поверхности широко используются в технике. Например, отражатель фары или прожектора должен иметь точную форму параболоида вращения, а ряд ферменных конструкций состоят из гиперболоидов вращения. Гиперболоид удобен тем, что его можно получить соединением прямолинейных стержней. На основе гиперболоидов инженером В.Г. Шуховым в 1922г. была построена знаменитая башня на ул. Шаболовка в Москве (Рис. 6 .38).

Рис. 6.38 – Шуховская башня – пример использования

гиперболоида вращения в технике.

5. Составные поверхности. Составную поверхность можно полностью определить, покрыв ее сеткой четырехугольных кусков (участков, ограниченных продольными и поперечными линиями на поверхности). Каждый такой кусок носит название поверхности Кунца (Coons patch) по имени проф. Стивена Кунца, разработавшего данный метод поверхностного моделирования в 1963 (Рис. 6 .39).

Рис. 6.39 – Поверхность Кунца.

Каждый кусок имеет геометрическую форму топологического прямоугольника (этот прямоугольник отличается от обычного тем, что его стороны не обязательно прямые и попарно перпендикулярные). Границы кусков представляют собой непрерывные кривые, что обеспечивает гладкость поверхности, натянутой на сетку. Внутренняя область каждого куска определяется методом интерполяции. Изображение составной поверхности, реализованное указанным способом, может быть получено на экране либо с помощью построения по точкам сплайновых кривых, либо путем создания многогранного каркаса, на который система будет автоматически аппроксимировать натяжение гладкой криволинейной поверхности.

Стороны каркаса чаще всего представляют собой NURBS-сплайны (nonuniform rational B-spline) – гладкие кривые, соединяющие заданные точки (Рис. 6 .40).

Рис. 6.40 – Сплайн и его физическое представление.

Под сплайном понимается линия наименьшего натяжения, проходящая через заданные точки. Сплайн имеет вполне реальное физическое воплощение в виде гибкой пластиковой полоски, при помощи которой в прошлом конструкторы строили плавные обводы судов и самолетов. Эта полоска и называлась сплайном.

Хотя методы поверхностного моделирования обладают многими достоинствами, существует ряд ограничений на их использование. Основными являются следующие ограничения:

• возникновение неоднозначности при попытке моделирования реального твердого тела;

• недостаточность точности представления некоторых поверхностных моделей для обеспечения надежных данных о трехмерных объемных телах;

• сложность процедур удаления скрытых линий и отображения внутренних областей.