Примеры решения задач

Пример 1. Метод Ритца для одномерного интеграла.

Пользуясь методом Ритца, найти экстремали функционала

.

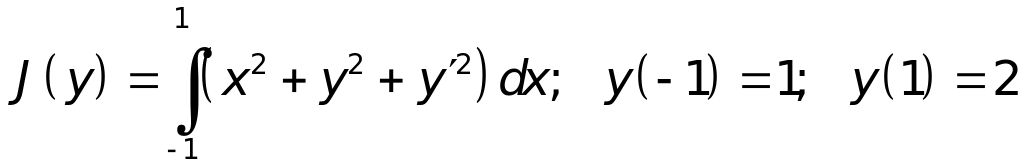Показать сходимость полученного приближенного решения к точному при возрастании числа элементов, используемых в аппроксимации. Построить графики решений.

Решение. Будем решать задачу в среде Maple. Определяем подынтегральную функцию:

> restart;

> F:=(x,y,y1)->x^2+y^2+y1^2;

Составим уравнение Эйлера для данного функционала. Для этого вычислим частные производные от F по y и y1 и полную производную по x от частной производной F по y1 (переменная y1 означает первую производную, а переменная y2 – вторую производную)

> dFdy:=diff(F(x,y,y1),y);dFdy1:=diff(F(x,y,y1),y1);

> d_dFdy1_dx:=diff(dFdy1,x);d_dFdy1_dy:=diff(dFdy1,y);

> d_Fdy1_dy1:=diff(dFdy1,y1);

Составим теперь уравнение Эйлера

> eq:=dFdy-d_dFdy1_dx-d_dFdy1_dy*y1-d_Fdy1_dy1*y2=0;

> eq:=simplify(lhs(eq)/2)=0;

> eq:=subs(y=y(x),y2=diff(y(x),x$2),lhs(eq))=0;

Решим полученное уравнение с заданными граничными условиями

> res:=dsolve({eq,y(-1)=1,y(1)=2},y(x));

> assign(res):y:=evalf(y(x));

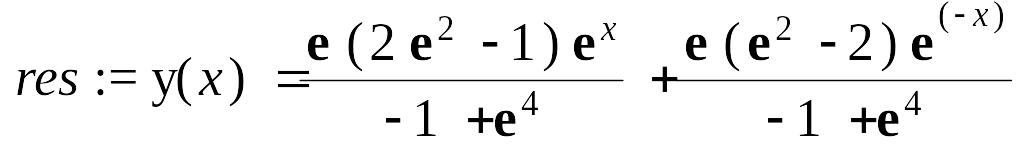
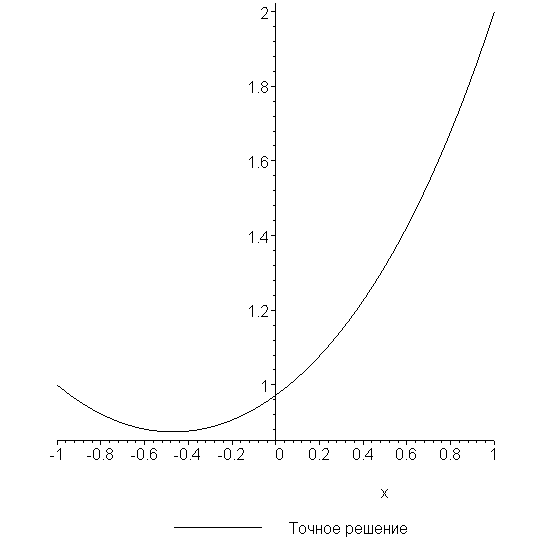
Построим график точного решения

> py:=plot(y,x=-1..1,legend=`Точное решение`,

color=black):

> plots[display]({py});

Решим теперь эту задачу с помощью пакета VariationalCalculus:

> with(VariationalCalculus);

Определяем подынтегральную функцию:

> y:='y':f:=x^2+y(x)^2+diff(y(x),x)^2;

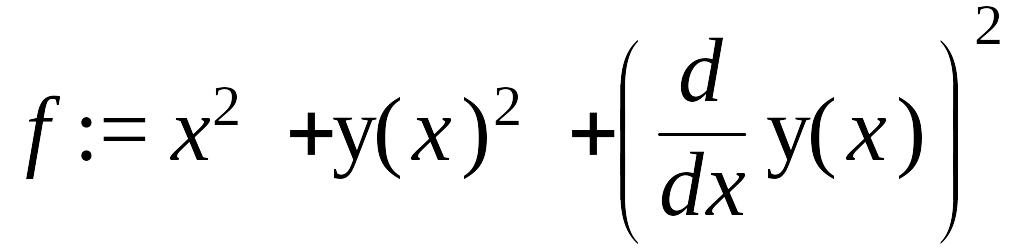
> EulerLagrange(f, x, y(x));

Решим уравнение Эйлера с заданными граничными условиями

> res1:=dsolve({op(%)=0,y(-)=1,y(1)=2},y(x));

assign(res1):y:=evalf(y(x));

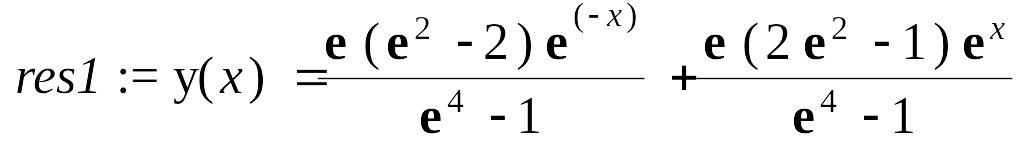
То есть, как и следовало ожидать, получили тот же результат!

Решаем теперь нашу задачу методом Ритца. Выбираем базисные функции и определяем аппроксимирующую функцию. Рассмотрим два варианта — аппроксимация полиномами и аппроксимация тригонометрическими функциями:

> phi0:=x->y1+(y2-y1)*(x-x1)/(x2-x1);

> phi:=(x,n)->sin(n*Pi*(x-x1)/(x2-x1));

> Us:=proc(x,N)option operator,arrow; local n;

phi0(x)+sum(a[n]*phi(x,n),'n'=1..N);

end proc;

> Up:=proc(x,N)option operator,arrow; local n;

phi0(x)+(x-x1)*(x-x2)*sum(a[n]*x^n,'n'=0..N);

end proc;

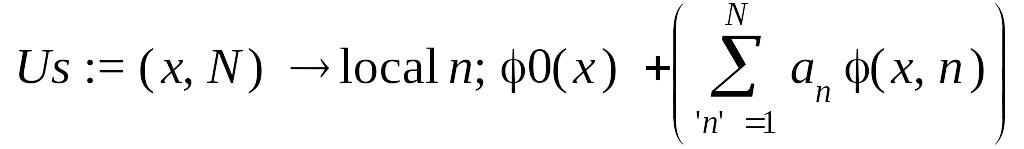
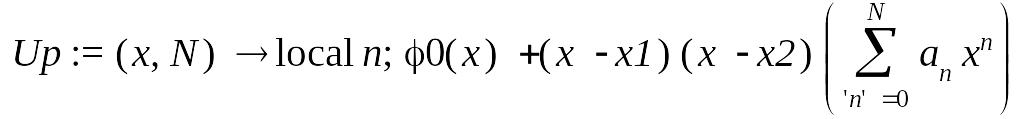
С целью автоматизации расчетов разработаем процедуру, формирующую и решающую систему уравнений метода Ритца, например, такую

> Ritz:=proc(F,u,i0,N,a)

local Fu,eqns,var,eq,i,res;global x1,x2;

Fu:=simplify(int(subs(y(x)=u,F),x=x1..x2)):

eqns:={}:var:={}:

for i from i0 to N do

var:=var union {a[i]}:

eq[i]:=diff(Fu,a[i])=0:

eqns:=eqns union {eq[i]}:

od:

res:=solve(eqns,var);

assign(res);

end proc:

Определим теперь нашу подынтегральную функцию

> F:=x^2+y(x)^2+diff(y(x),x)^2;

Зададим граничные точки

> x1:=-1;x2:=1;y1:=1;y2:=2;

Задаемся числом аппроксимирующих функций и решаем задачу

> N:=3:c1:=`cross`:c2:=`circle`:c3:=`box`:

> for j from 1 to N do

a:=array(1..j):u:=Us(x,j):

Ritz(F,u,1,j,a);

pUs_||j:=

plot(Us(x,j),x=-1..1,

color=black,style=point,symbol=c||j,

legend=cat(`Метод Ритца N = `,convert(j,string))):

end do:

Отображаем решение на графиках

> plots[display]({pUs_1,pUs_2,pUs_3,py});

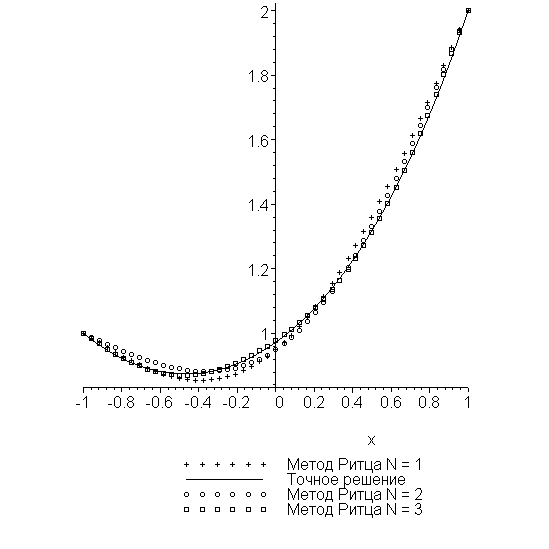
Видим, что удержание трех членов ряда вполне достаточно. Покажем эти аппроксимации

> Us(x,1);Us(x,2);Us(x,3);

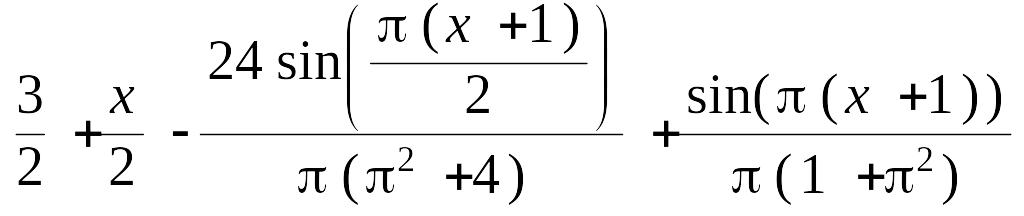
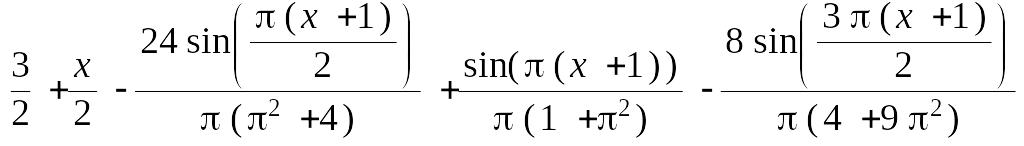
Рассмотрим теперь решение задачи с помощью аппроксимации полиномами

> N:=2:c1:=`cross`:c2:=`circle`:

> c3:=`box`:c0:=`diamond`:

> for j from 0 to N do

a:=array(0..j):u:=Up(x,j):

Ritz(F,u,0,j,a);

pUp_||j:=

plot(Up(x,j),x=-1..1,color=black,

style=point,symbol=c||j,

legend=cat(`Метод Ритца N = `,convert(j,string))):

end do:

Отобразим решение на графиках

> plots[display]({pUp_0,pUp_1,pUp_2,py});

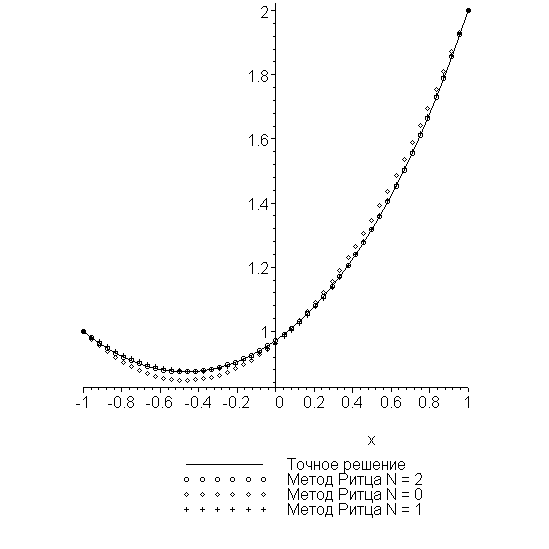
Видим, что и в этом случае удержание трех членов ряда вполне достаточно. Покажем полученные аппроксимации

> Up(x,0);Up(x,1);Up(x,2);

Пример 2. Конечно-разностный метод Эйлера.

Найти приближенное решение задачи о минимуме функционала

.

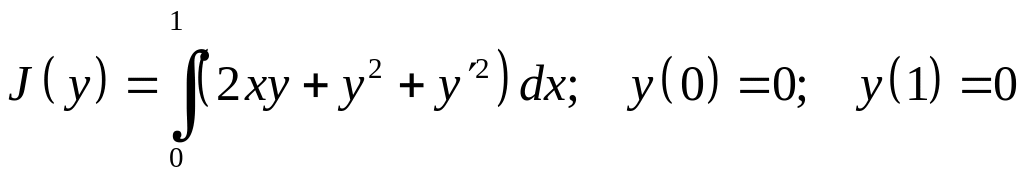Показать сходимость полученного приближенного решения к точному при возрастании числа элементов, используемых в аппроксимации. Построить графики решений.

Решение. Будем решать задачу в среде Maple. Аппроксимация подынтегральной функции конечными разностями:

> restart; interface(displayprecision = 5):

> F:=proc(Y,m,h)

(Y[m+1]-Y[m])^2/h^2+Y[m]^2+2*X[m]*Y[m]

end proc;

Интеграл заменяем суммой по формуле прямоугольников

> S1:=proc(h,F,N) options operator, arrow;

h*(sum(F(Y,i,h),i = 0 .. N-1))

end proc;

Задаем пределы интегрирования:

> a := 0; b := 1;

Выбираем число узловых точек и определяем шаг интегрирования:

> N:=10: h:=(b-a)/N;

Вычисляем абсциссы вершин ломаной

> for j from 0 to N do X[j] := a+j*h end do:

Функционал как функция ординат вершин ломаной:

> Phi:=S1(h,F,N);

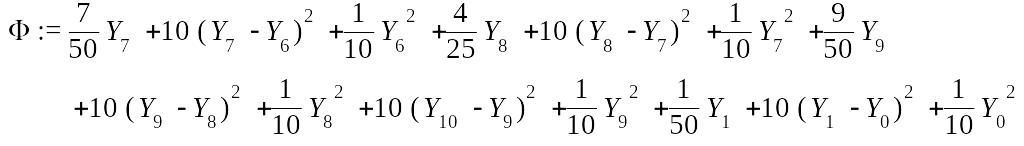
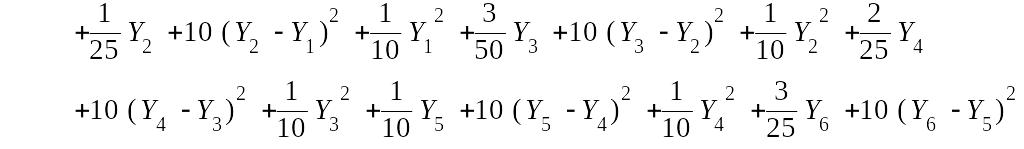
Учет граничных условий:

> Y[0]:=0; Y[N]:=0; Phi;

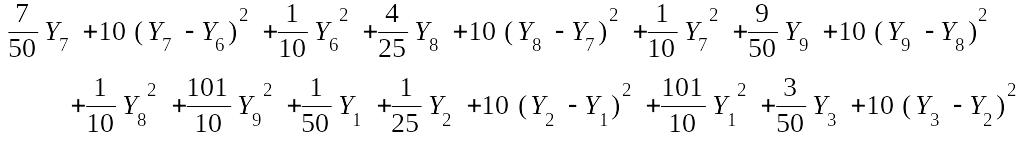
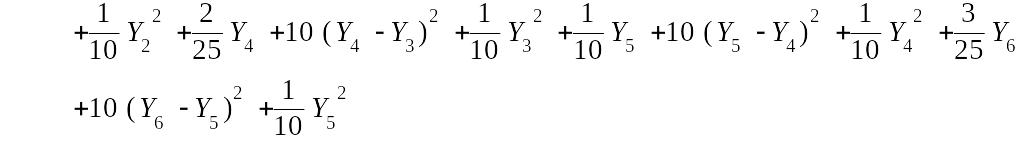
Составляем минимизирующую систему уравнений:

> for k to N-1 do

eq[k]:=evalf(diff(Phi,Y[k]))=0

end do:

var := {}: eqns := {}:

for k to N-1 do

var:=`union`(var,{Y[k]}):

eqns := `union`(eqns, {eq[k]}):

end do:

nops(var); nops(eqns);

Решаем систему:

> res:=solve(eqns, var);assign(res):

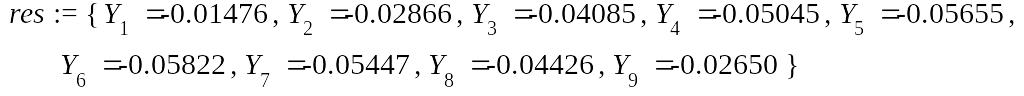
Сформируем список точек вершин ломаной:

> for j from 0 to N do P[j]:=[X[j],Y[j]] end do:

L:=[seq(P[k-1],k = 1 .. N+1)]:

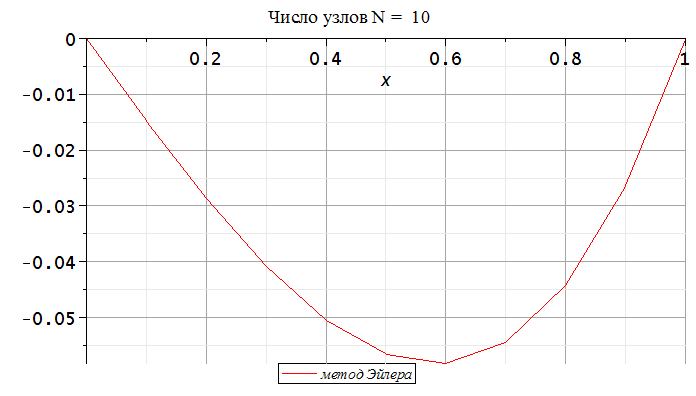
Построим график решения:

> plot(L,x=0..1,title=cat("Число узлов N = ",

convert(N, string)),titlefont=[roman,15],

labelfont[Helvetica,roman,14],

legend=["метод Эйлера"],gridlines=true);

Для сравнения найдем точное решение задачи.

> with(VariationalCalculus):

> f:=(diff(y(x),x))^2+y(x)^2+2*x*y(x);

> ode:=EulerLagrange(f,x,y(x));

> problem := `union`(ode, {y(0) = 0, y(1) = 0});

> dsolve(problem, y(x));

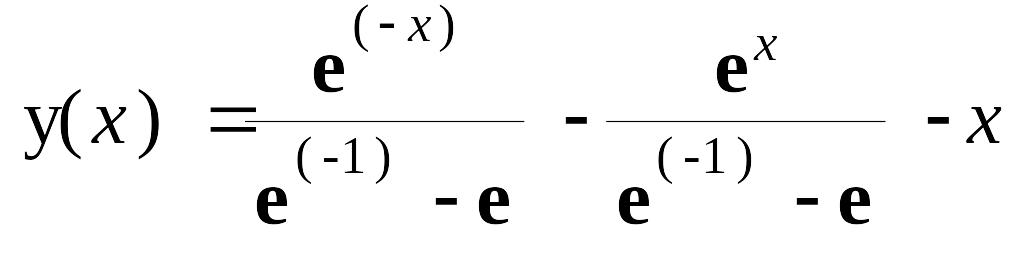
> simplify(convert(%, trig));

> y := unapply(rhs(%), x);

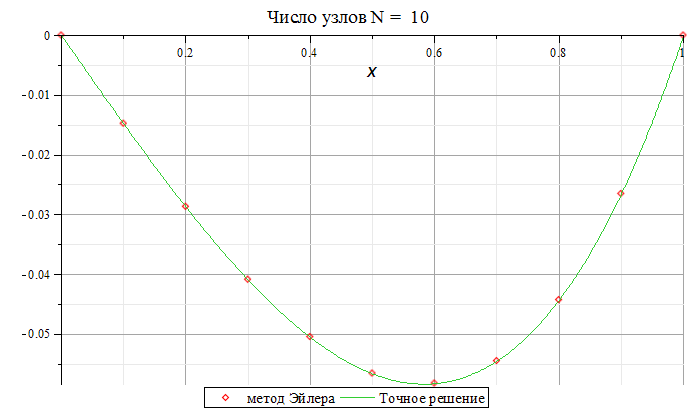
Построим графики приближенного и точного решений:

> plot([L, y(x)],x=0..1,

title=cat("Число узлов N = ",

convert(N, string)),titlefont=[roman,15],

style=[point,line],labelfont[Helvetica,roman,14],

legend=["метод Эйлера","Точное решение"],

gridlines=true);

Пример 3. Метод Ритца для двойного интеграла.

Используя метод Ритца, найти экстремали функционала

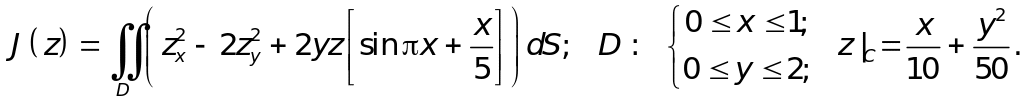
Исследовать сходимость. Построить графики.

Решение. Будем решать задачу в среде Maple. Выбираем базисные функции и определяем аппроксимирующую функцию:

> restart;

> phi0:=(x,y)->x/10+y^2/50;

> phi:=(x,y,i,j)->

sin(i*Pi*(x-x1)/(x2-x1))*sin(j*Pi*(y-y1)/(y2-y1));

> U:=proc(x,y,M,N)option operator,arrow;

local n,m;

phi0(x,y)+

sum(sum(a[m,n]*phi(x,y,m,n),'m'=1..M),'n'=1..N);

end proc;

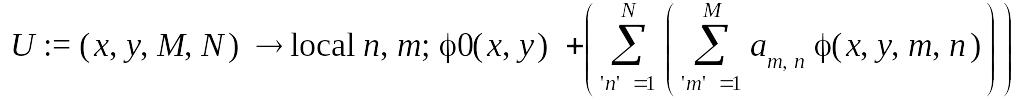
Здесь также удобно разработать процедуру для автоматического составления и решения уравнений метода Ритца. Например, такую

> Ritz:=proc(F,M,N,a)local Fu,eqns,var,eq,i,j,res;

Fu:=simplify(int(int(F,x=0..1),y=0..2));

eqns:={}:var:={}:

for i from 1 to M do

for j from 1 to N do

var:=var union {a[i,j]}:

eq[i,j]:=diff(Fu,a[i,j])=0:

eqns:=eqns union {eq[i,j]}:

od:

od:

res:=solve(eqns,var);

assign(res);

end proc:

Вводим теперь граничные точки

> x1:=0;x2:=1;y1:=0;y2:=2;

Определяем подынтегральную функцию

> F:=diff(u(x,y),x)^2-2*diff(u(x,y),y)^2+

2*y*u(x,y)*(sin(Pi*x)+x/5);

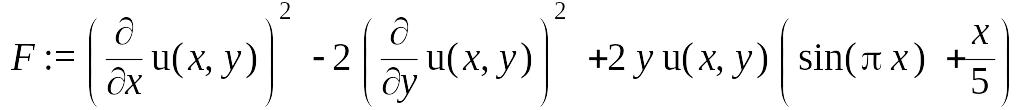
Задаемся числом аппроксимирующих функций и решаем задачу

> M:=2:N:=2:a:=array(1..M,1..N):

> F2:=subs(u(x,y)=U(x,y,M,N),F):Ritz(F2,M,N,a):

Посмотрим результат на графике

> p||M:=

> plot(U(0.5,y,M,N),y=0..2,color=black,linestyle=4,

legend=cat(`M=N=`,convert(M,string))):

plots[display]({p2});

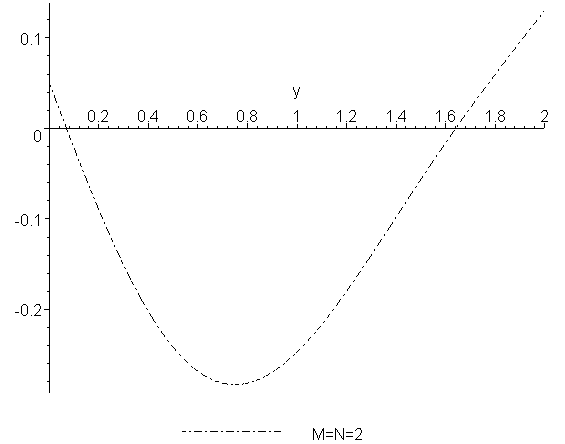
Увеличим на единицу (по каждой переменной) число слагаемых в аппроксимации и повторим расчет

> M:=3:N:=3:a:=array(1..M,1..N):

> F3:=subs(u(x,y)=U(x,y,M,N),F):Ritz(F3,M,N,a):

> p||M:=

plot(U(0.5,y,M,N),y=0..2,color=black,linestyle=1,

legend=cat(`M=N=`,convert(> M,string))):

> plots[display]({p2,p3});

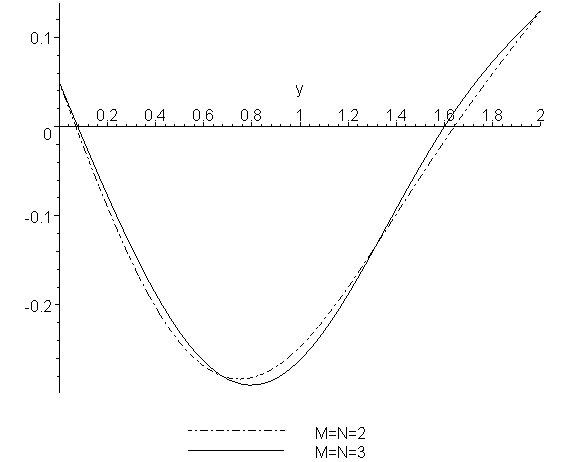
> M:=4;N:=4;a:=array(1..M,1..N):

> F4:=subs(u(x,y)=U(x,y,M,N),F):Ritz(F4,M,N,a);

> p||M:=

plot(U(0.5,y,M,N),y=0..2,color=black,linestyle=3,

legend=cat(`M=N=`,convert(M,string))):

> plots[display]({p2,p3,p4});

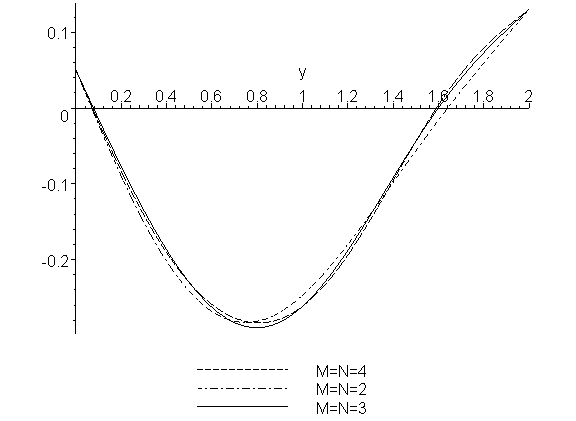
Видим, что приближенные решения хорошо сходятся, и можно ограничиться значениями M = N = 4.

Пример 4. Уравнение Эйлера для двойного интеграла.

Решить вариационную задачу для функционала, если на контуре области функция принимает заданные значения:

.

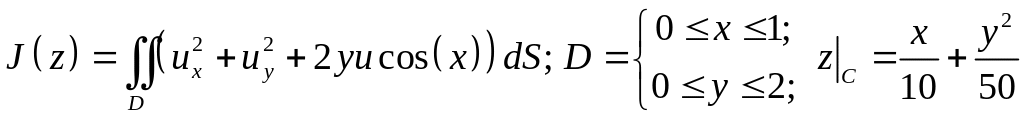Решение. Будем решать задачу в среде Maple. Определим подынтегральную функцию. Для удобства обозначим производные функции по и по соответственно, через и :

> F:=proc(x,y,u,ux,uy) options operator, arrow;

ux^2+uy^2+2*y*u*cos(x)

end proc;

Уравнение Эйлера в этих обозначениях имеет вид:

.

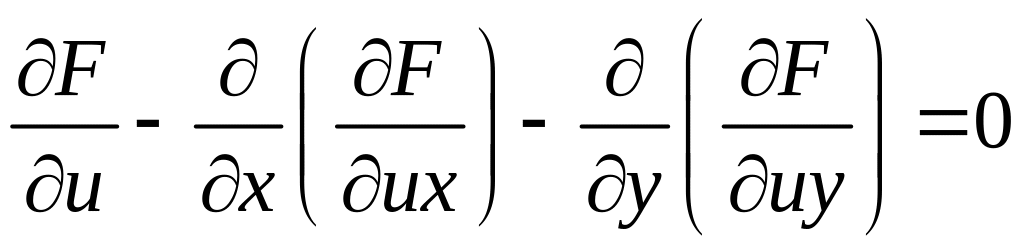Вычисляем последовательно производные в этом уравнении

> a1:=diff(F(x,y,u,ux,uy),u);

a2:=diff(F(x,y,u,ux,uy),ux);

a3:=diff(F(x,y,u,ux,uy),uy);

Составляем уравнение Эйлера для функционала

> EulerEq:=a1-(diff(subs(ux=diff(u(x,y),x),a2),x))-

(diff(subs(uy=diff(u(x,y),y),a3),y))=0;

Таким образом, получили следующее уравнение

> pde:=-(1/2)*op(2,lhs(EulerEq))-

(1/2)*op(3,lhs(EulerEq))=(1/2)*op(1,lhs(EulerEq));

Сформируем теперь граничные условия. Для этого определим граничную функцию

> f:=proc(x,y) options operator, arrow;

(1/10)*x+(1/50)*y^2

end proc;

Определяем граничные условия:

> bc:=u(0,y)=f(0,y),u(1,y)=f(1,y),

u(x,0)=f(x,0),u(x,2)=f(x,2);

Таким образом, задача математической физики поставлена: найти функцию , удовлетворяющую дифференциальному уравнению

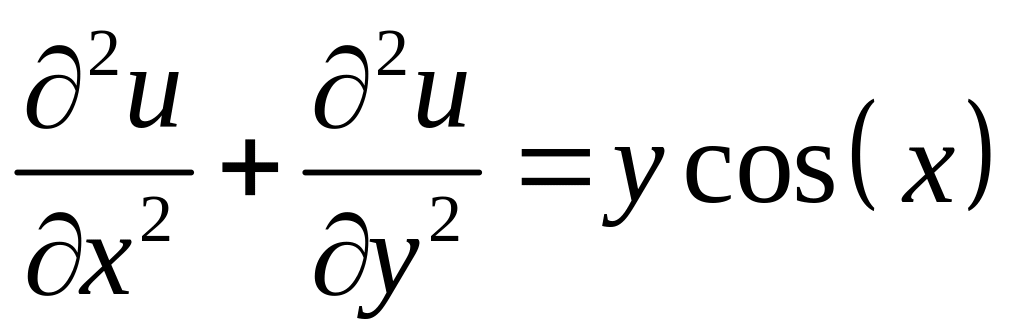
в прямоугольнике , и принимающую заданные значения на границе этого прямоугольника

,

.

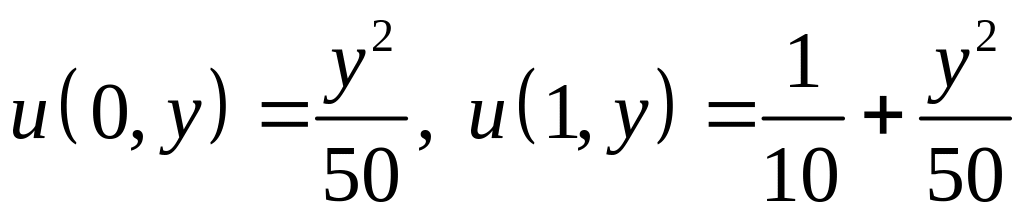Сформулированная задача классифицируется как задача Дирихле для уравнения Пуассона в прямоугольнике [1]. Это — неоднородная задача, причем неоднородности присутствуют как в граничных условиях, так и в уравнении.

Чтобы построить решение задачи разобьем ее на две вспомогательные задачи. А именно, будем искать решение задачи в виде суммы двух функций: . Функции и определим как решения следующих задач.

Задача 1: найти функцию , удовлетворяющую дифференциальному уравнению

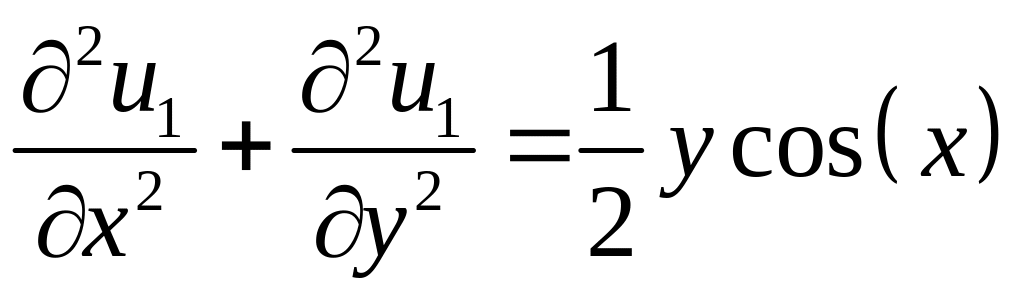
и граничным условиям

,

.

Задача 2: найти функцию , удовлетворяющую дифференциальному уравнению

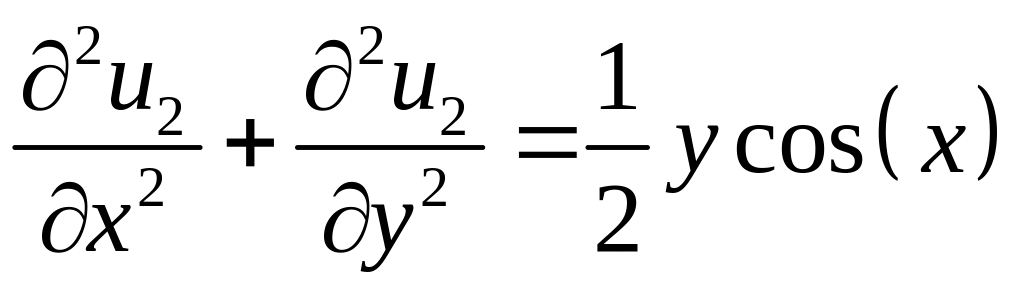
и граничным условиям

,

.

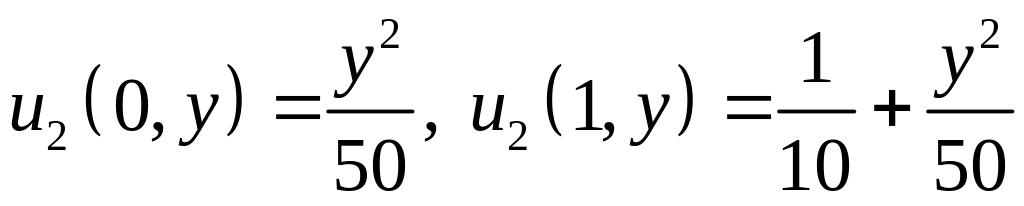Определим эти задачи в Maple.

Задача 1:

> pde1:=diff(u1(x,y),x,x)+diff(u1(x,y),y,y)=

(1/2)*y*cos(x);

bc1:=u1(0,y)=0,u1(1,y)=0,

u1(x,0)=f(x,0),u1(x,2)=f(x,2);

Задача 2:

> pde2:=diff(u2(x,y),x,x)+diff(u2(x,y),y,y)=

(1/2)*y*cos(x);

bc2:=u2(0,y)=f(0,y),u2(1,y)=f(1,y),

u2(x,0)=0,u2(x,2)=0;

Очевидно, решение исходной задачи будет

> u:=proc(x,y) options operator, arrow;

u1(x, y)+u2(x, y)

end proc;

Проверим это. Подставим функцию в уравнение

> simplify(pde, {pde1, pde2});

Как видим, получили тождество. Проверим выполнение граничных условий

> bc;

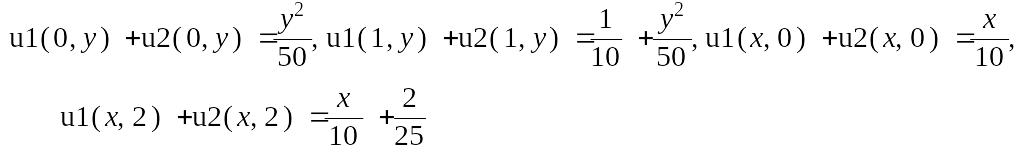
Таким образом, условия на функцию тоже выполняются.

Рассмотрим задачу 1. Будем решать ее методом Гринберга [1]. Соответствующая задача Штурма-Лиувилля

очевидно, имеет решение[1]

> X:=proc(x,n) options operator, arrow;

sin(n*Pi*x)

end proc;

lambda:=proc(n) options operator, arrow;

n^2*Pi^2

end proc;

Действительно, подставим это решение в уравнение

> Diff(X(x,n),x,x)+lambda(n)*X(x,n) = 0;value(%);

Проверим выполнение граничных условий

> X(0,n)=0,X(1,n)=0;simplify(%,assume=integer);

Решение задачи 1, в соответствии с методом Гринберга, представим в виде ряда по собственным функциям задачи Штурма-Лиувилля

.

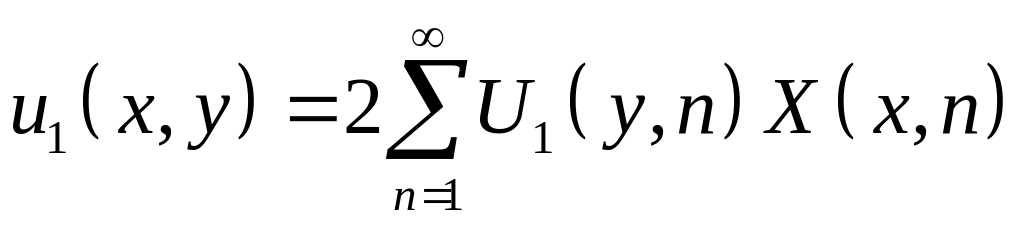Здесь учтено, что квадрат нормы собственных функций равен :

.

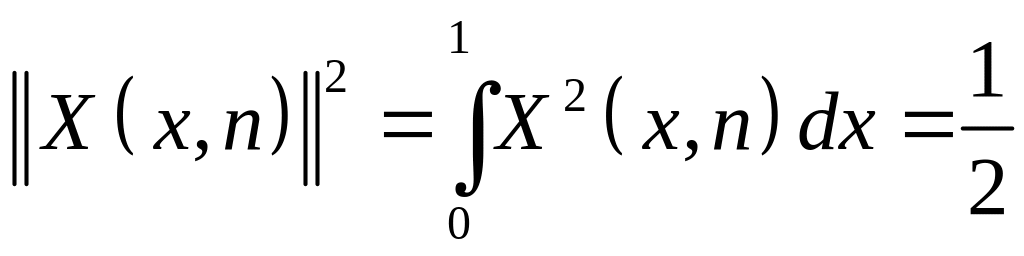Действительно,

> int(X(x, n)^2, x = 0 .. 1);

simplify(%, assume = integer);

Уравнение для трансформанты получим, умножив исходное уравнение в частных производных на и проинтегрировав на отрезке :

> int(lhs(pde1)*X(x,n),x = 0 .. 1) =

int(rhs(pde1)*X(x,n),x = 0 .. 1);

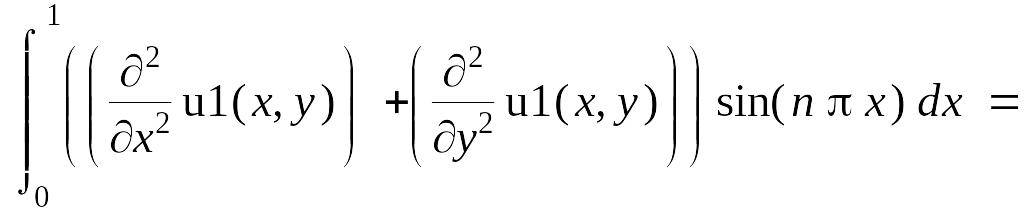
> intPDE1 := simplify(%, assume = integer);

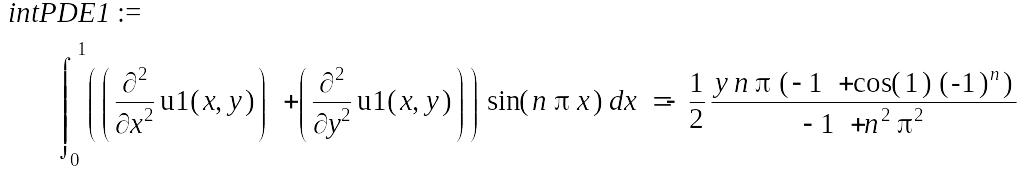
Преобразуем правую часть полученного уравнения

> LHS1:=IntegrationTools[Expand](lhs(intPDE1));

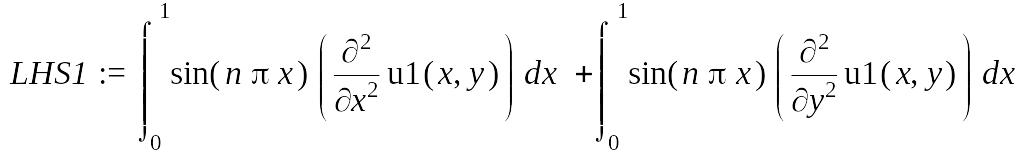
Первый интеграл берем по частям два раза:

> IntegrationTools[Parts](op(1, LHS1), sin(n*Pi*x));

I1 := simplify(%, assume = integer);

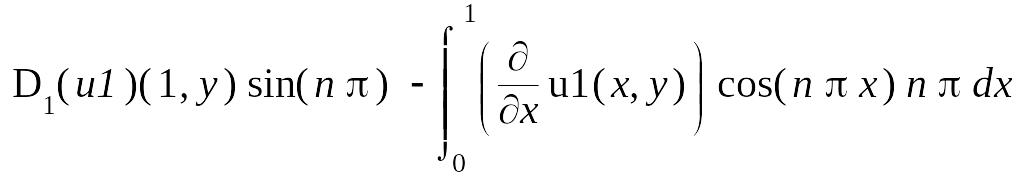
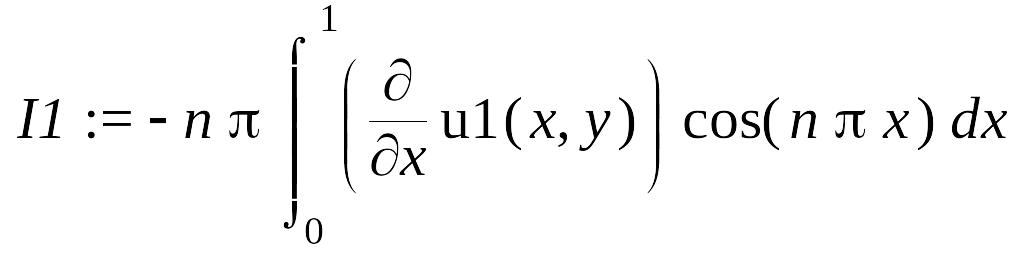
> IntegrationTools[Parts](I1, cos(n*Pi*x));

I1 := simplify(%, assume = integer);

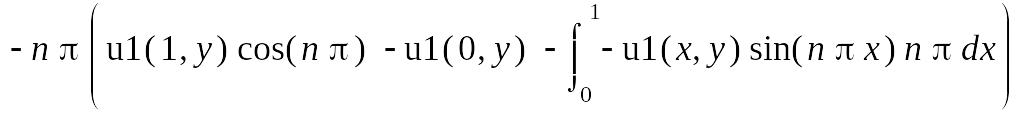
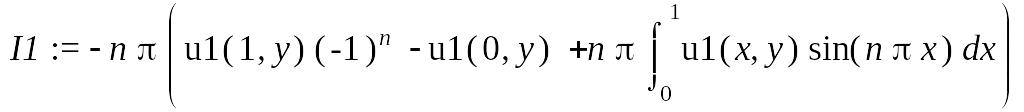
Учтем граничные условия

> I1 := simplify(I1, {bc1});

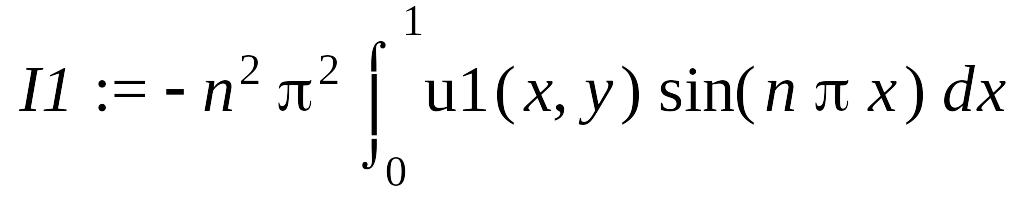
Итак, первый интеграл с учетом преобразовался в выражение

> I1 := subs(op(4, I1) = U1(y, n), I1);

Второй интеграл в выражении LHS1 есть, очевидно,

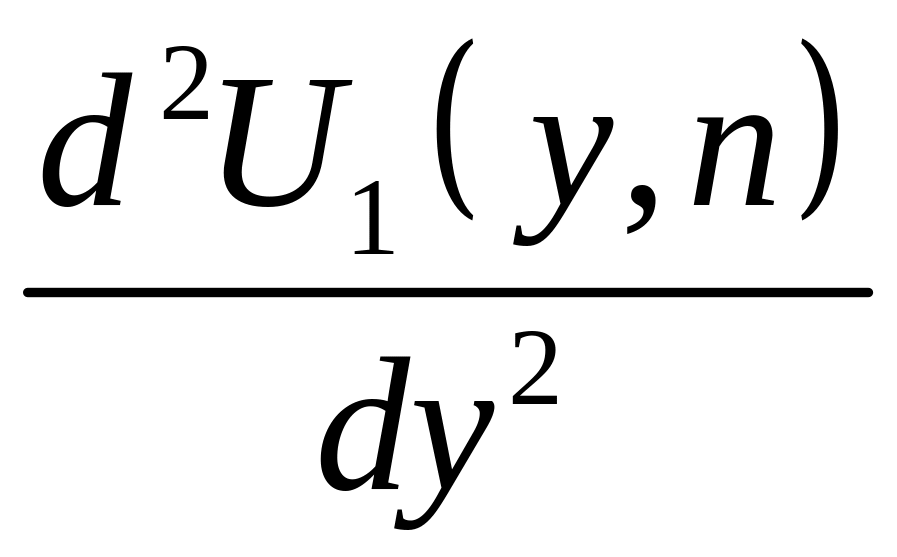
> I2:=subs(op(2,LHS1)=diff(U1(y,n),y,y),op(2,LHS1));

Таким образом, уравнение для трансформанты получено:

> ode1 := I2+I1 = rhs(intPDE1);

Сформируем граничные условия

> int(lhs(bc1[3])*X(x,n),x = 0 .. 1) =

int(rhs(bc1[3])*X(x,n),x = 0 .. 1);

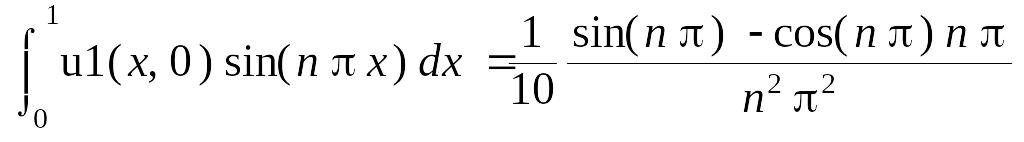
> bcODE1:=simplify({subs(lhs(%) = U1(0,n), %)},

assume = integer);

> int(lhs(bc1[4])*X(x,n),x = 0 .. 1) =

int(rhs(bc1[4])*X(x,n),x = 0 .. 1);

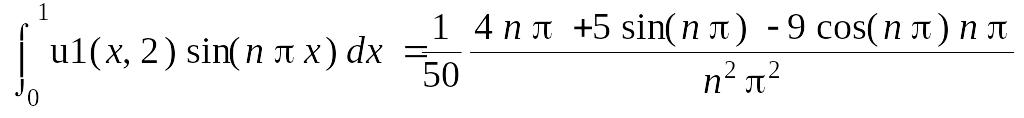
> simplify({subs(lhs(%) = U1(2,n), %)},

assume = integer);

> bcODE1 := `union`(bcODE1, %);

Находим трансформанту

> res := dsolve(ode1, U1(y, n));

Удобно записать общее решение ОДУ так

> V1:=proc(y) options operator, arrow;

C1*sinh(n*Pi*y)+C2*sinh(n*Pi*(2-y))+

(-1+cos(1)*(-1)^n)*y/(-2*n*Pi+2*n^3*Pi^3)

end proc;

Проверим

> subs(U1(y,n) = V1(y), ode1);

simplify(subs(U1(y,n) = V1(y), ode1));

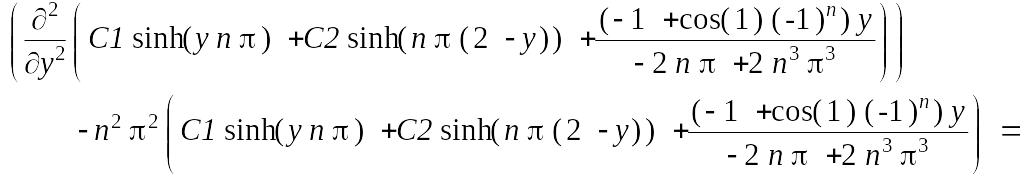
Все в порядке!

Формируем систему уравнений по граничным условиям

> subs({U1(0,n) = V1(0), U1(2,n) = V1(2)}, bcODE1);

Решаем систему

> solve(%, {C1, C2}); assign(%):

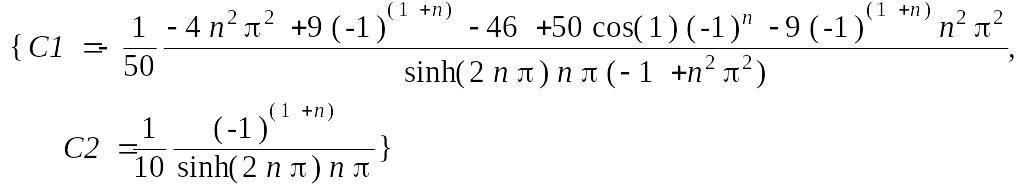
Проверка:

> subs(U1(y,n) = V1(y), ode1): simplify(%);

Итак, трансформанта найдена:

> U1 := unapply(V1(y), y, n);

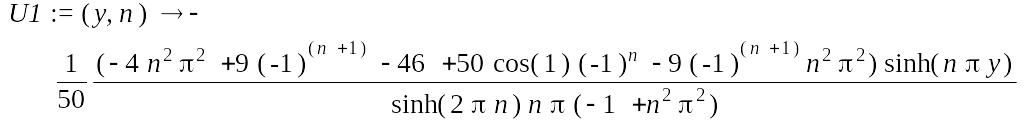
Решение задачи 1 дается следующим рядом

> u1:=proc(x,y) options operator, arrow;

2*(Sum(U1(y, n)*X(x, n), n = 1 .. infinity))

end proc;

> u1(x,y);

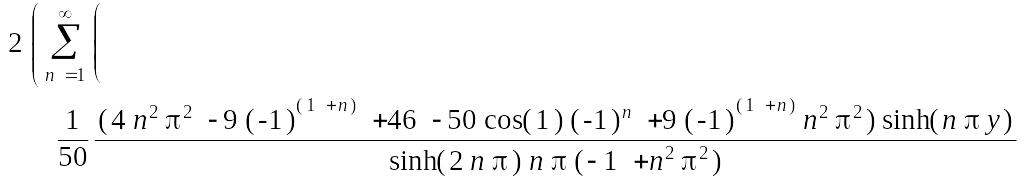
Проверим найденное решение. Подставим решение в уравнение; отдельно рассмотрим левую и правую части уравнения. Левая часть:

> LHSpde := combine(lhs(pde1)); RHSpde := rhs(pde1);

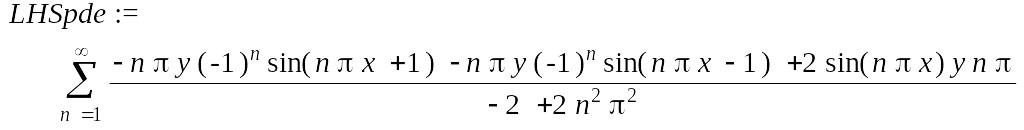
Упростим левую часть уравнения:

> op(1, LHSpde);

> numer(op(1, LHSpde));

> expand(%);

> factor(%);

Таким образом, левая часть ДУЧП имеет вид

> LHSpde:=Sum(-2*Pi*n*y*sin(n*Pi*x)*(-1+cos(1)*

(-1)^n)/(-2+2*n^2*Pi^2), n=1..infinity);

Правая часть уравнения:

> RHSpde := rhs(pde1);

Покажем, что левая часть уравнения совпадает с правой частью, т. е.

> 1/2*y*cos(x)=Sum(-2*Pi*n*y*sin(n*Pi*x)*(-1+cos(1)*

(-1)^n)/(-2+2*n^2*Pi^2),n = 1 .. infinity);

Для этого разложим функцию в ряд по собственным функциям на отрезке . Коэффициенты разложения:

> 2*int(1/2*y*cos(x)*sin(n*Pi*x), x = 0 .. 1);

simplify(%, assume = integer);

Таким образом, уравнение выполняется.

Проверим выполнение граничных условий.

Граничные условия по переменной :

> simplify(u1(0,y), assume = integer);

simplify(u1(1,y), assume = integer);

Граничные условия по переменной :

> u1(x,0);

Это — разложение граничной функции в ряд по функциям на отрезке . Действительно, коэффициенты разложения

> 2*int(f(x,0)*sin(n*Pi*x), x = 0 .. 1);

simplify(%, assume = integer);

Далее,

> u1(x,2);

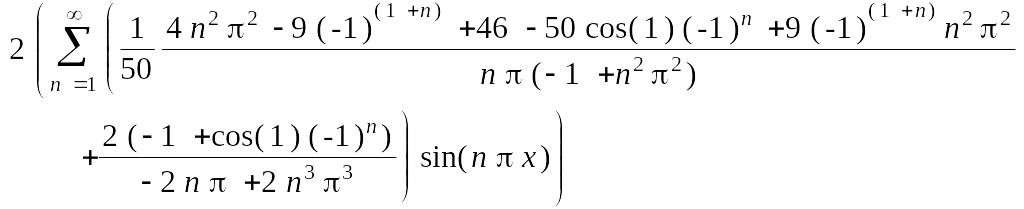
Это — разложение граничной функции в ряд по функциям на отрезке . Действительно, преобразуем общий член ряда

> q:=op(2, u1(x,2));

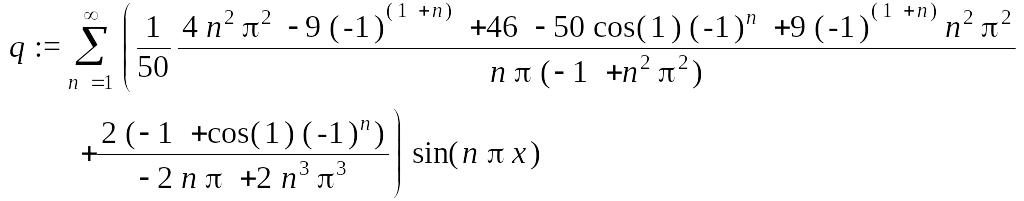
> q:=op(1,q);

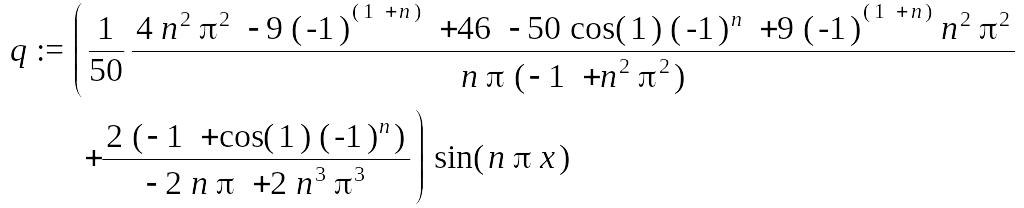
> op(1,q);

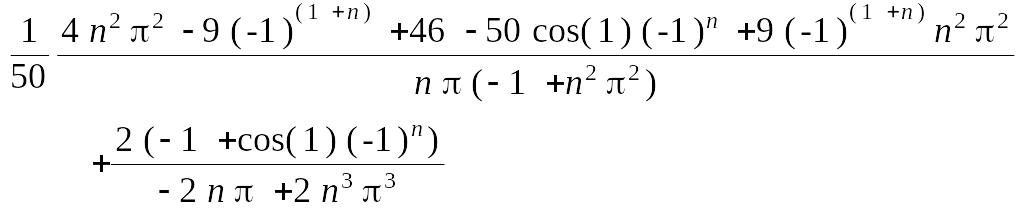
> q:=%: combine(q);

Таким образом, мы имеем ряд

> 'u1(x,2)'=2*Sum(%*sin(n*Pi*x),n=1..infinity);

Коэффициенты разложения граничной функции в ряд по функциям на отрезке :

> 2*int(f(x,2)*sin(n*Pi*x), x = 0 .. 1);

simplify(%, assume = integer);

что и требовалось доказать.

Итак, решение задачи 1 найдено. Читателю предлагается построить решение задачи 2 самостоятельно, в качестве упражнения. Приведем формулу этого решения, полученную в Maple

,

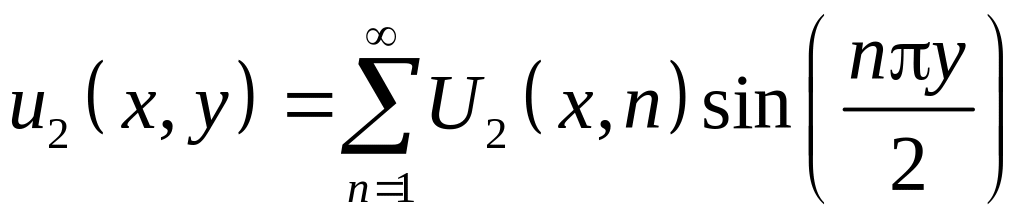где

.

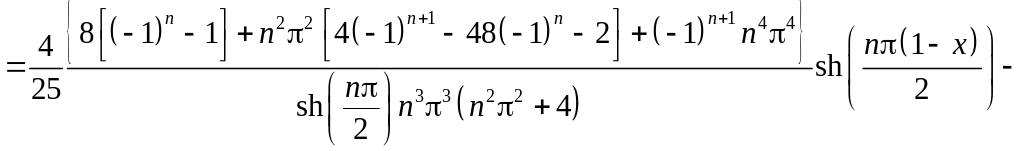
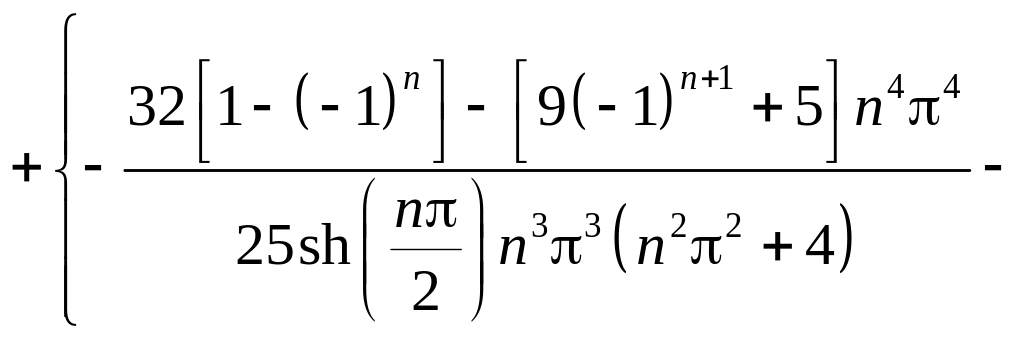
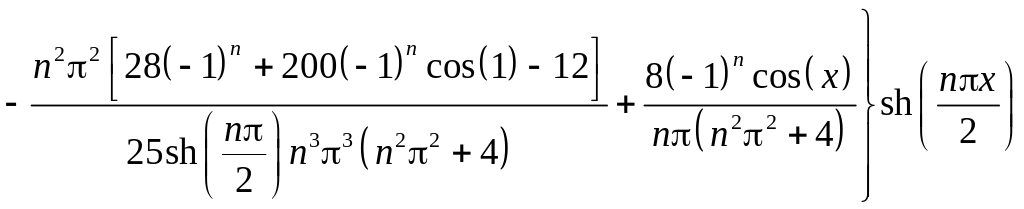Окончательно решение задачи дается суммой решений задачи 1 и задачи 2: .