7. Диференціювання функцій, заданих неявно та параметрично.

Похідна функції, заданої параметрично рівняннями: обчислюється за формулою

Приклад 9.

Знайти та від функції, заданої параметрично: .

Розв’язання.

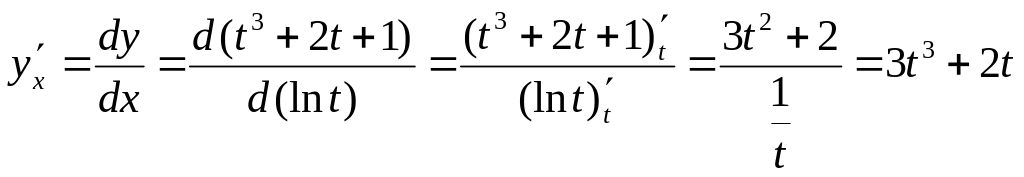
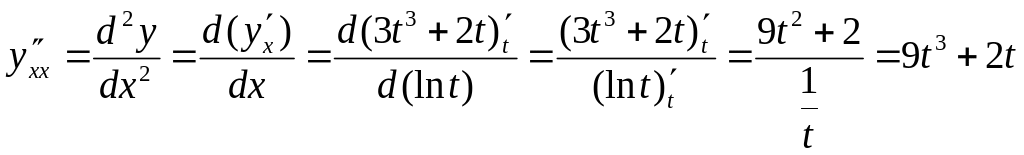Похідна неявної функції.

Якщо залежність між х та у задана в не явній формі , то для знаходження похідної треба:

1. Обчислити похідну по х від лівої та правої частин заданого рівняння , вважаючи у функцією х. Отримаємо .

2. Розв’язати останнє рівняння відносно .

Приклад 10

Знайти та від функції, заданої неявно рівнянням .

Розв’язання.

Диференціюємо ліву та праву частину рівняння: ,

вважаючи, що . Згідно з правилом диференціювання складної функції, маємо: або .

Звідси .

Далі диференціюємо ліву та праву частину рівняння: , вважаючи, що .

Маємо

Звідси

Враховуючи вираз для , отримуємо:

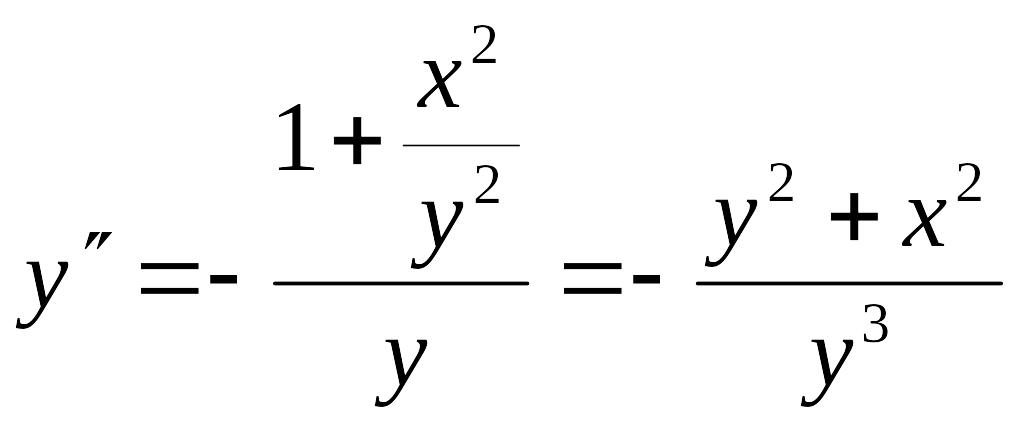
Але згідно з умовою , отже остаточно маємо: .

2. Дослідження функцій та побудова графіків.

1. Зростання та спадання функції.

Означення 4. Функція називається зростаючою на інтервалі , якщо для і таких, що виконується нерівність .

Означення 5. Якщо ж при виконується нерівність , то функція називається спадною.

Теорема 7.

Якщо на , то функція зростає на цьому інтервалі.

Якщо на , то функція спадає на цьому інтервалі.

Інтервали спадання та зростання функції називаються інтервалами монотонності.

2. Екстремуми функцій.

Означення 6. Точка називається точкою локального максимуму функції , якщо існує такий окіл точки , що для виконується нерівність .

Означення 7. Аналогічно точка – точка локального мінімуму функції , якщо для виконується нерівність .

Точки локального максимуму та локального мінімуму функції називається точками локального екстремуму цієї функції.

Теорема 8. Необхідна умова екстремуму.

Якщо функція диференційована в точці і має в цій точці екстремум, то .

Означення 8. Точка , в якій називається стаціонарною.

Означення 9. Точки, в яких , нескінченності або не існує, називають критичними точками.

Теорема 9.

Достатні умови екстремуму.

Нехай функція диференційована в деякому околі критичної точки , за виключенням, можливо, самої точки . Тоді, якщо:

а) і , то - точка локального максимуму функції ;

б) і , то - точка локального мінімуму функції ;

в) не змінює знака при , то точка не є точкою локального екстремуму.

3. Опуклість, вгнутість. Точки перетину.

Нехай диференційована функція на інтервалі .

Означення 10. Графік функції називається опуклим уверх або опуклим на інтервалі , якщо він розташований нижче дотичної, проведеної в будь-якій точці цього інтервалу.

Означення 11. Графік функції називається вгнутим униз, або вгнутим на інтервалі , якщо він розташований вище дотичної, проведеної в будь-якій точці цього інтервалу.

Точка графіка функції, яка відділяє його опуклу частину від вгнутої, називається точкою перегину.

Теорема 10. Достатня умова опуклості (вгнутості) графіка функції.

Нехай функція двічі диференційована на інтервалі . Тоді, якщо:

а) на , то графік функції є опуклим на ;

б) на , то графік функції є вгнутим на .

Із означення точки перегину та достатніх умов опуклості (вгнутості) випливає, що, коли – абсциса точки перегину графіка функції , то друга похідна дорівнює нулю, нескінченності або не існує.

Точки, в яких , нескінченності або не існують, називаються критичними точками другого роду.