
- •Інститут економіки та нових технологій Кафедра прикладної математики та математичного моделювання
- •Наклад 50 примірників Передмова
- •І. Основні питання, що вивчаються в розділі.
- •1. Диференціювання функцій.
- •2. Дослідження функцій та побудова графіків.
- •Іі. Основні теоретичні відомості. Приклади розв’язання задач.
- •1. Диференціювання функцій.
- •1. Означення похідної.
- •2. Зв’язок між неперервністю та диференційованістю функції. Теорема 1.
- •3. Означення диференціала.
- •4. Основні правила диференціювання.
- •5. Похідні основних елементарних функцій.
- •7. Диференціювання функцій, заданих неявно та параметрично.
- •1. Зростання та спадання функції.
- •2. Екстремуми функцій.
- •Теорема 8. Необхідна умова екстремуму.
- •Теорема 9.
- •3. Опуклість, вгнутість. Точки перетину.
- •Теорема 10. Достатня умова точки перегину.
- •4. Асимптоти.
- •5. Схема повного дослідження функції.
- •Приклад 10
- •6. Знаходження найбільшого та найменшого значення функції на відрізку.
- •Завдання 2.
- •Варіанти завдань.
- •Завдання 3
- •Варіанти завдань.
- •Завдання 4.
- •Варіанти завдань.
- •Завдання 5.
- •Варіанти завдань.
- •V. Список використаної і рекомендованої літератури.
2. Зв’язок між неперервністю та диференційованістю функції. Теорема 1.
Якщо функція
диференційована
в деякій точці
![]() ,
то вона в цій точці неперервна.
,
то вона в цій точці неперервна.
Наслідок. З цієї теореми випливає, що неперервність функції є необхідною умовою диференційованості функції. Це означає, що в точках розриву функція не має похідних, тобто вона не диференційована.
Функція, яка неперервна в
точці
,
може бути не диференційованою в цій
точці. Наприклад, функція
![]() неперервна в точці
неперервна в точці
![]() ,
але не має похідної в цій точці тому, що
,
але не має похідної в цій точці тому, що
![]() , а
, а
![]() ,
тобто границя відношень
,
тобто границя відношень
![]() залежить від способу прямування
залежить від способу прямування
![]() .
.
3. Означення диференціала.
Нехай функція
диференційована в інтервалі
![]() ,
,
![]()
Згідно з означенням похідної
функції
маємо:
![]()
Змінна величина відрізняється
від своєї границі на нескінченно малу
![]() ,
тому
,
тому
![]()
![]() (**)
(**)
Функція диференційована в
точці
,
тому вона неперервна в цій точці, але
тоді при
величини
![]() та
та
![]() будуть нескінченно малими. Порядок
малості цих трьох величин різний:
будуть нескінченно малими. Порядок
малості цих трьох величин різний:
![]() мають
однаковий порядок малості, а величина
є нескінченою малою вищого порядку
малості. Отже, при
мають
однаковий порядок малості, а величина
є нескінченою малою вищого порядку
малості. Отже, при
![]() перший
додаток у правій частині рівності (**) є
головною частиною приросту функції.
Він є лінійним відносно
.
перший
додаток у правій частині рівності (**) є
головною частиною приросту функції.
Він є лінійним відносно
.
Означення 3.
Головну лінійну частину приросту
функції називають диференціалом цієї
функції. Диференціал функції
назначають
![]() або
або
![]() .
.
Таким чином,
![]() .
.
Одержимо:
![]() ,
тобто похідна функції дорівнює відношенню
диференціала функції до диференціала
незалежної змінної.
,
тобто похідна функції дорівнює відношенню
диференціала функції до диференціала
незалежної змінної.
4. Основні правила диференціювання.
Правила сформулюємо у вигляді теорем.
Теорема 2.
Похідна постійної величини
С дорівнює нулю, тобто
![]() .
.
Теорема 3.
Якщо кожна
із функцій
![]() n-
скінчене число) диференційована в деякій
точці
,
то їх алгебраїчна сума також є
диференційованою в цій точці, причому
похідна алгебраїчної суми цих функцій
дорівнює такій самій алгебраїчній сумі
їх похідних, тобто
n-
скінчене число) диференційована в деякій
точці
,
то їх алгебраїчна сума також є
диференційованою в цій точці, причому
похідна алгебраїчної суми цих функцій
дорівнює такій самій алгебраїчній сумі
їх похідних, тобто
![]()
Доведення.
Нехай
![]() і аргумент
одержує приріст
.
Тоді
і аргумент
одержує приріст
.
Тоді
![]() також одержує приріст:
також одержує приріст:
![]()
Згідно з властивостями границі
і з тим, що існують похідні функцій
![]() маємо,
що
існує, причому
маємо,
що
існує, причому
![]() .
.
Підставивши значення , одержимо: , що і треба було довести.
Аналогічно можна довести наступні теореми.
Теорема 4.
Якщо кожна з функцій
![]() та
та
![]() диференційовані в точці
,
то добуток цих функцій також має похідну
в точці
,
причому цю похідну находять за формулою:
диференційовані в точці
,
то добуток цих функцій також має похідну
в точці
,
причому цю похідну находять за формулою:
![]()
Теорема 5.
Якщо
та
мають похідні в точці
і
![]() то частка цих функцій також має похідну
в точці
,
яку знаходять за формулою:
то частка цих функцій також має похідну
в точці
,
яку знаходять за формулою:
![]() .
.
Теорема 6.
Якщо
![]() і функція
і функція
![]() та
та
![]() диференційо-вані функції своїх аргументів,
то існує похідна по
складної функції
,
причому вона дорівнює добутку похідної
функції
по проміжному аргументу
диференційо-вані функції своїх аргументів,
то існує похідна по
складної функції
,
причому вона дорівнює добутку похідної
функції
по проміжному аргументу
![]() та похідної функції
по аргументу
,
тобто
та похідної функції
по аргументу
,
тобто
![]()
5. Похідні основних елементарних функцій.
Таблиця основних формул диференціювання.
1.![]() 2.
2.
![]() .
.
3.
![]() .
4.
.
4.![]() .
.
5.
![]() 6.
6.![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.![]()
11.
![]() 12.
12.![]()
13.
![]()
Тут
![]() .
Якщо
.
Якщо
![]() ,
то
,
то
![]()
Приклади 1-6.
Знайти похідні функції.
Приклад 1
![]()
Розв’язання.
Застосовуємо правило
диференціювання суми функцій, маємо:
![]()
Приклад 2
![]()
Розв’язання.
Застосовуючи правило диференціювання добутку функції, маємо:
![]()
Приклад 3
![]()
Розв’язання.
Застосовуючи правило диференціювання частки функції, маємо:
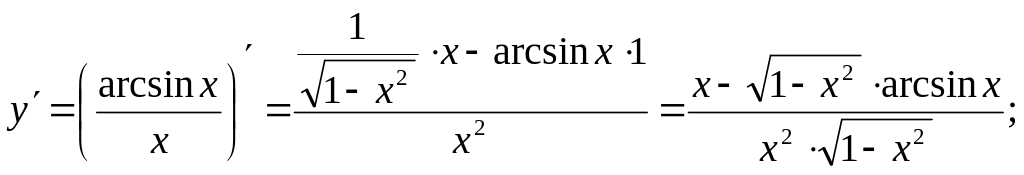
Приклад 4
![]()
Розв’язання.
Застосовуючи правило
диференціювання складної функції,
степеневої функції та суми, маємо:
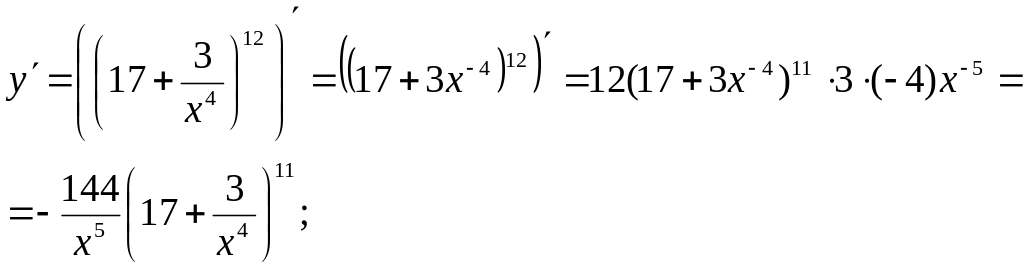
Приклад 5
![]()
Розв’язання.
Застосовуючи правило
диференціювання складної функції,
логарифмічної функції та суми, маємо:![]()
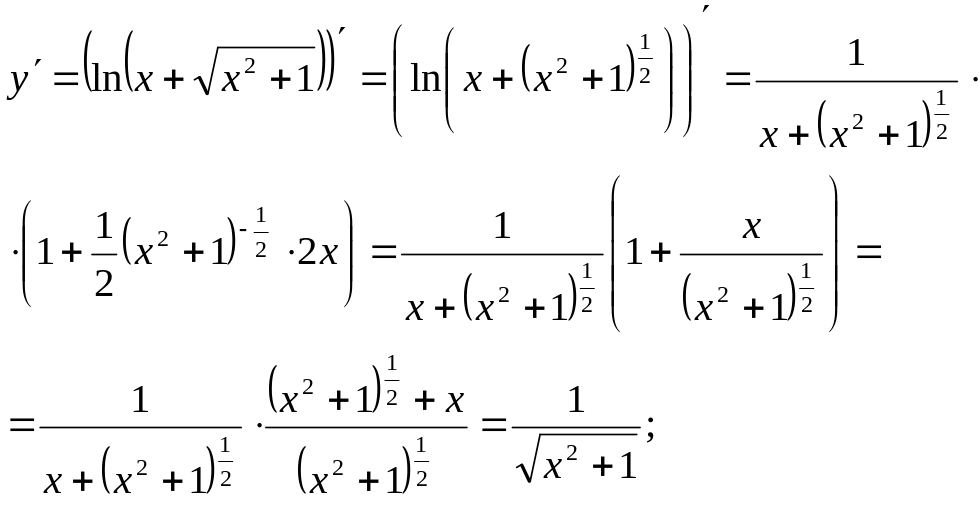
Приклад 6
![]()
Розв’язання.
Перепишемо задану функцію у
вигляді:
![]() .
Тоді
.
Тоді
![]() .
.
Логарифмічне диференціювання.
Логарифмічною похідною
функції
![]() називається похідна від логарифму цієї
функції, тобто
називається похідна від логарифму цієї
функції, тобто
![]() .
Послідовне застосування логарифмування
та диференціювання функції називається
логарифмічним диференціюванням.
.
Послідовне застосування логарифмування
та диференціювання функції називається
логарифмічним диференціюванням.
Приклад 7.
Знайти похідну функції
![]() .
.
Розв’язання.
Маємо складну показникові функцію, бо і основа, і степінь залежить від .
Прологарифмуємо задану
функцію
![]() .
.
Маємо:
![]()
Далі диференціюємо обидві
частини останньої рівності по
:
![]()
Звідси
![]()
Далі знаходимо
![]() :
:
![]() або
або
![]() .
.
Приклад 8.
Знайти похідну функції:
![]()
Розв’язання.
Запишемо задану функцію у
вигляді:
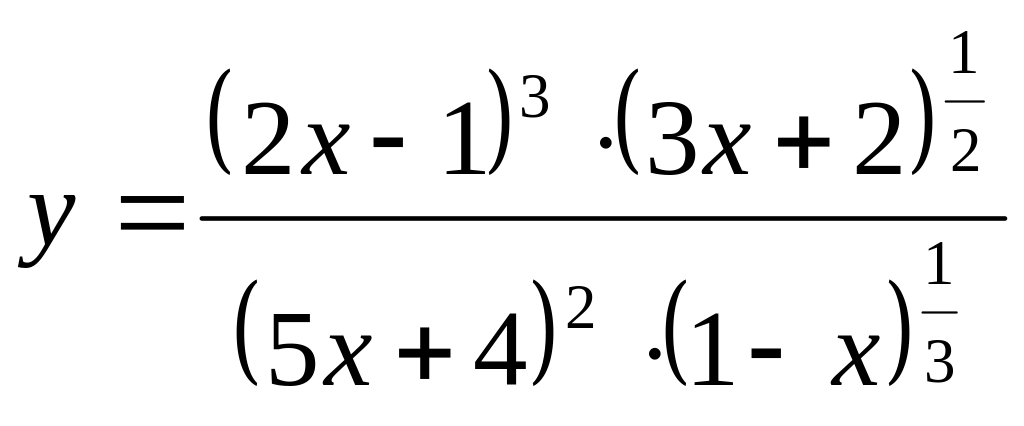 .
.
Прологарифмуємо задану функцію:
![]()
Про диференціюємо обидві
частини останньої рівності по
:
![]() .
.
Звідси
![]()
![]() .
.
Отже,
![]()
