1.13. Применение теоремы Гаусса для расчета электрических полей

Если заряд распределен равномерно и симметрично, то применение теоремы Гаусса упрощает расчет электрического по заданному распределению заряда. Характерные примеры расчета приведены в учебнике И.В. Савельева «Курс общей физики. Электричество и магнетизм», п. 1.14:

а) поле бесконечной однородно заряженной плоскости.

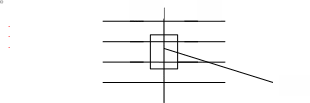
Рис. 1.22.

Согласно теореме Гаусса,

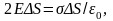
откуда

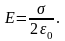
б) поле двух равномерно заряженных плоскостей.

Рис. 1.23.

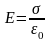
- между обкладками, и вне плоского конденсатора.

в) поле бесконечного заряженного цилиндра.

Рис. 1.24.

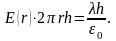
г) поле заряженной сферической поверхности

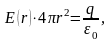
откуда

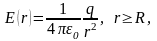(1.55)

где - радиус сферической поверхности. Поле между обкладками сферического конденсатора также описывается формулой (1.55).

д) поле объемно-заряженного шара.

Поле равномерно заряженного шара радиуса вне шара описывается формулой (1.55), а внутри шара применение теоремы Гаусса

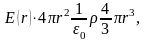
заряд шара

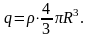
Тогда

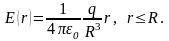
1.14. Формула Гаусса-Остроградского и

формулировка закона Кулона в дифференциальной форме

Запишем скалярное произведение двух векторов – оператора Гамильтона и гладкой векторной функции . Эта операция порождает производное скалярное поле, называемое дивергенция поля :

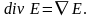(1.56)

В отличие от потока векторного поля (1.53) дивергенция не интегральная, а дифференциальная характеристика этого поля. Дивергенция характеризует мощность источников поля.

Выразим дивергенцию поля в декартовой системе координат:

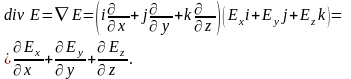(1.57)

Формула Гаусса-Остроградского связывает мощность источников с потоком порождаемого ими векторного поля:

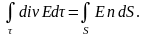(1.58)

Иначе говоря, формула Гаусса-Остроградского связывает интеграл по объему от дивергенции вектора с потоком этого вектора через замкнутую поверхность, ограничивающую объем. Согласно теореме Гаусса (см. (1.54)), имеем:

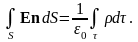(1.59)

Из (1.58) и (1.59) следует

Последнее равенство справедливо тождественно независимо от выбора объема , поэтому

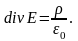(1.60)

Выполнение (1.60), как и теоремы Гаусса (1.54), обусловлено справедливостью закона Кулона. Значит, уравнение (1.60) выражает формулировку закона Кулона в дифференциальной форме.

Линейность уравнения (1.60) отражает справедливость принципа суперпозиции для напряженности электрического поля. В теории электромагнетизма принято, что (1.60) справедливо не только для неподвижных зарядов, но и для произвольно движущихся зарядов.

1.15. Основная задача электростатики. Уравнения Пуассона и Лапласа

Основная задача электростатики состоит в определении напряженности электрического поля по заданному распределению источников поля - неподвижных электрических зарядов. В общем случае решение такой задачи упрощается, если его проводить в два этапа:

1) сведение задачи к решению дифференциального уравнения для потенциала;

2) нахождение напряженности поля по уже найденному потенциалу.

Чтобы получить уравнение для потенциала, подставим выражение потенциала 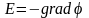в (1.60). Найдем

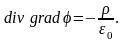(1.61)

Учтем 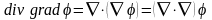. Скалярное произведение двух векторных операторов Гамильтона порождает скалярный дифференциальный оператор второго порядка – оператор Лапласа:

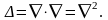(1.62)

В декартовых координатах оператор Лапласа записывается как

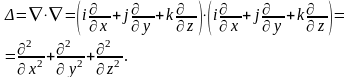(1.63)

С учетом (1.62) из (1.61) следует уравнение Пуассона

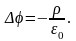(1.64)

После решения уравнения Пуассона (1.64) относительно потенциала по заданному распределению плотности заряда можно найти напряженность поля по формуле .

При переходе от дискретного к непрерывному распределению зарядов формула

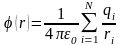(1.24)

для потенциала поля системы зарядов заменяется формулой

(1.65)

Выражение (1.65) является решением уравнения Пуассона (1.64), если все заряды сосредоточены в объеме конечной величины. Формулы (1.24) и (1.65) предполагают нормировку потенциала на нуль в бесконечности. Само уравнение Пуассона при решении не предполагает обязательного использования именно этой нормировки.

Решение основной задачи электростатики оказывается однозначным. Это следует из однозначности решения прямой задачи электромагнетизма о нахождении электромагнитного поля по заданным источникам поля, граничным и начальным условиям для поля.

Решение обратной задачи электростатики (нахождение распределения источников поля - зарядов по электрическому полю, заданному в конечном объеме) в общем случае неоднозначно.

Пример. Однородно заряженный шар создает вне своего объема такое же электрическое поле, как и точечный заряд, равный заряду шара и помещенный в точку центра шара.

Если в области пространства, где требуется найти электрическое поле, заряды отсутствуют (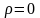 ), то уравнение Пуассона (1.64) превращается в уравнение Лапласа

(1.66)

Для решения уравнения Лапласа, как и уравнения Пуассона, должны быть заданы граничные условия для потенциала. Эти условия задаются на поверхности, ограничивающей область, где надо найти потенциал.