3.7. Примеры на построение линий по их уравнениям

Пример 16 [1, к задачам № 51-60, п. а, в, с]. Даны уравнения линий на плоскости:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Установить, какая линия определяется каждым уравнением, и сделать схематический рисунок.

Решение

1. Уравнение 3х – 4у – 12 = 0 является частным случаем уравнения (16), поэтому оно определяет прямую линию. Для построения этой прямой найдём точки пересечения с осями координат:

– при х = 0 получим ;

– при у = 0 получим .

Следовательно, точками пересечения будут точки Р₁ (0; –3) и Р₂(4; 0). Прямая изображена на рис. 8.

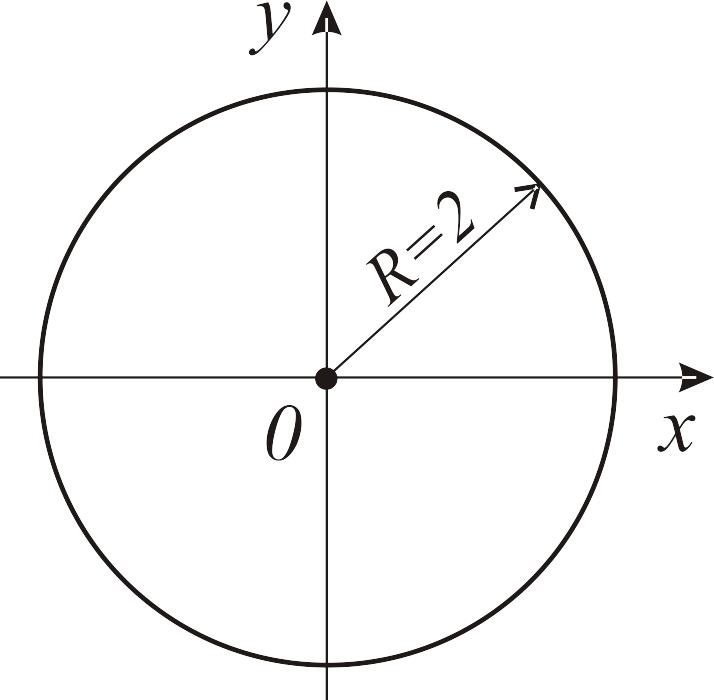
2. Уравнение х² + у² = 4 (рис. 9) определяет окружность с центром в начале координат и радиусом R = 2 (см. табл. 4, п. 1).

Рис. 8. Графическое представление линии

Рис. 9. Графическое представление окружности

3. Уравнение х² + у² – 6х + 8у + 16 = 0 не совпадает ни с одним из уравнений, приведённых в табл. 4. Приведём его к виду (22).

Для этого сгруппируем слагаемые, содержащие только х и только у, дополнив их до полных квадратов: (х – а)² и (у – в)².

В результате получим

(х² – 6х + 9) – 9 + (у² + 8у + 16) – 16 + 16 = 0

или

(х – 3)² + (у + 4)² = 9.

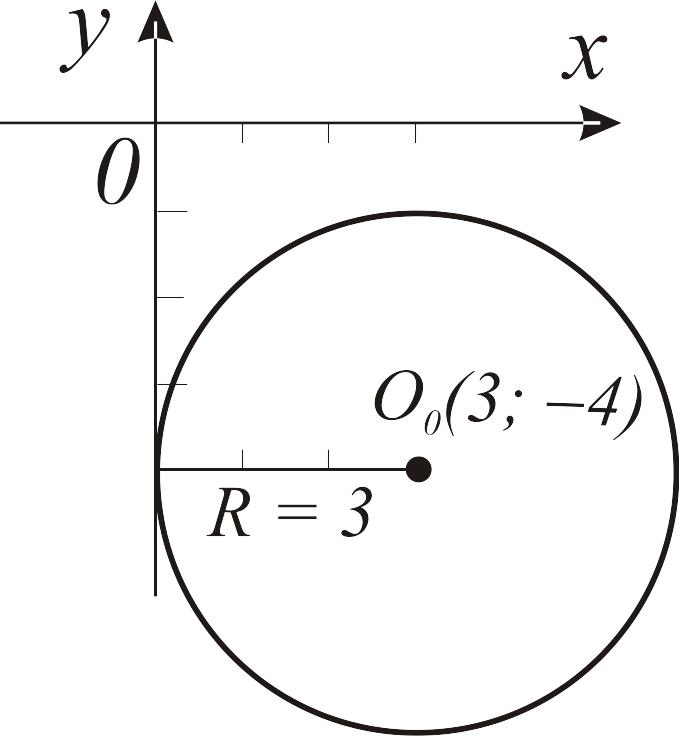
Это уравнение является частным случаем (22), поэтому определяет окружность с центром в точке О₀ (3; –4) и радиусом R = 3 (рис. 10).

4. Уравнение 4х² + 25у² = 100 приведем к каноническому виду. Разделив обе части этого равенства на 100, получим уравнение

.

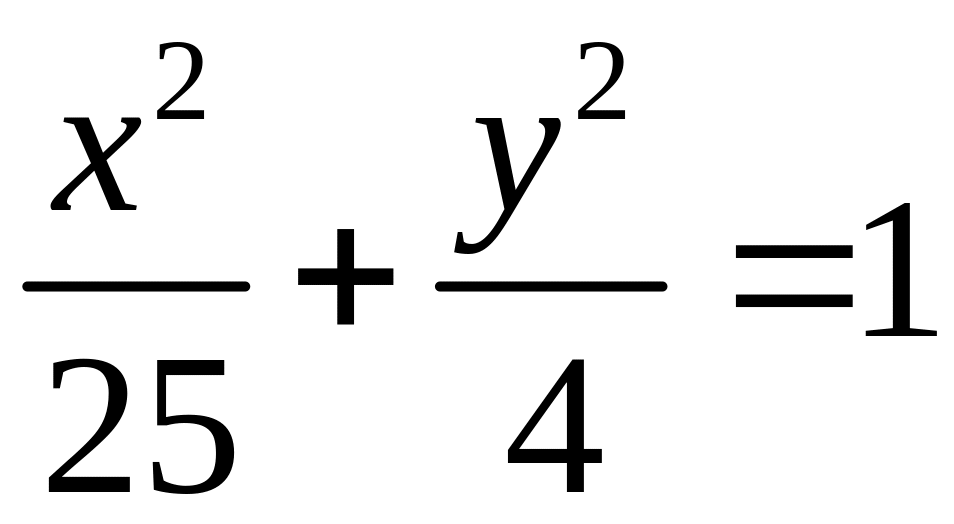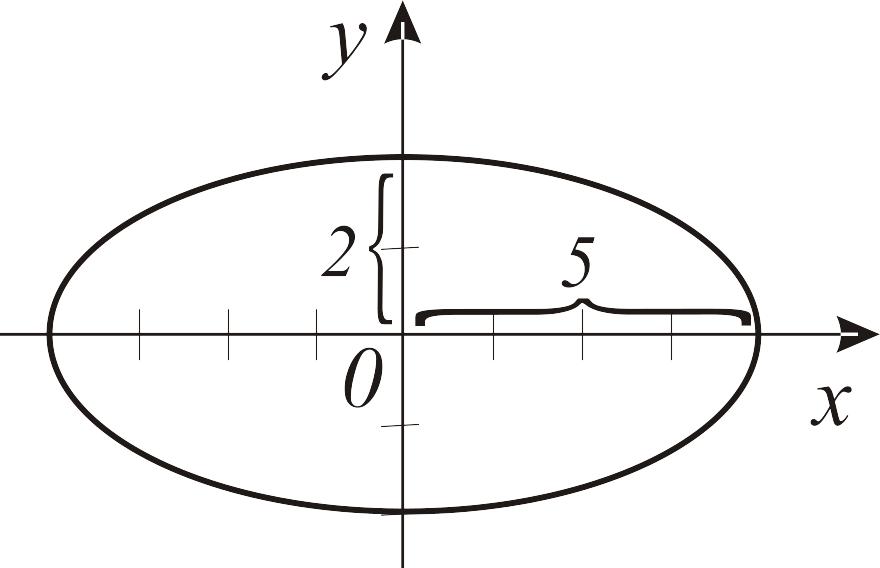
Согласно таблице 4, п. 2, это простейшее уравнение эллипса с полуосями а = 5 и в = 2. Изображаем его на рис. 11.

Рис. 10. Графическое представление окружности с центром в точке О0 (3; –4)

Рис. 11. Графическое представление эллипса

5. Аналогично поступим с уравнением 4х² – у² = 4. Разделив обе части на 4, как и в предыдущем пункте, получим каноническое уравнение гиперболы с полуосями а = 1, в = 2 (рис. 12):

.

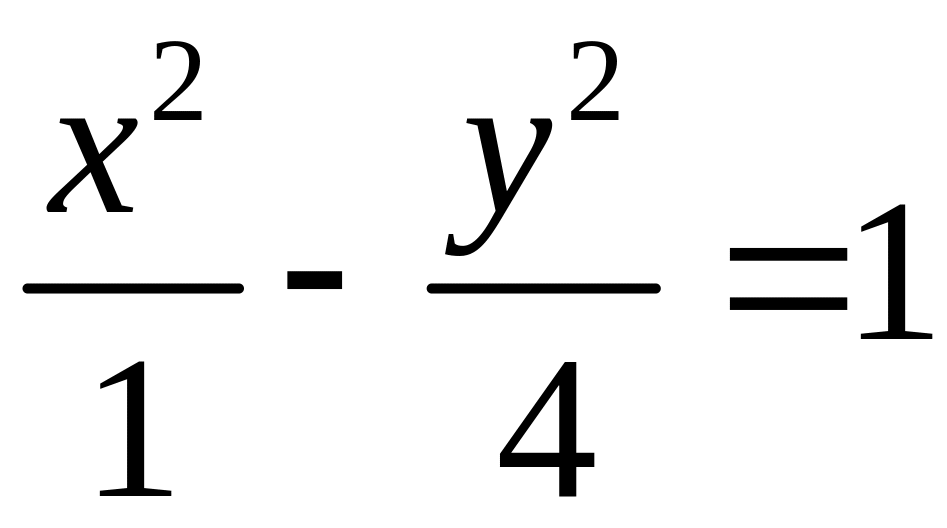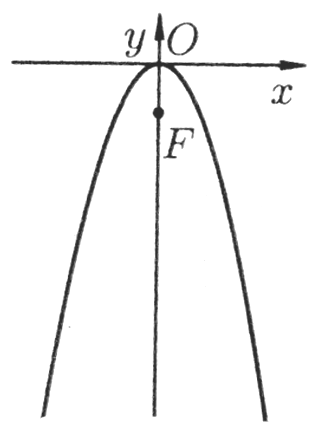
6. Запишем уравнение х² + 6у = 0 в виде х² = –6у. Это уравнение параболы с параметром р = –3, с вершиной О(0; 0) и осью симметрии 0у. Фокус параболы F (0; –3/2). Парабола изображена на рисунке 13 (см. табл. 4, п. 4.1).

Рис. 12. Графическое представление гиперболы

Рис. 13. Графическое представление параболы

3.8. Понятие уравнения поверхности в пространстве

Пусть задана поверхность S и введена прямоугольная система координат 0хуz (рис. 14).

Рис. 14. Графическое представление поверхности в пространстве

Уравнением поверхности S относительно системы 0хуz называют уравнение

F(x, y, z) = 0, (23)

которому удовлетворяют координаты всех точек, лежащих на этой поверхности, и не удовлетворяют координаты точек, не лежащих на ней.

Например, для всех точек плоскости х0у аппликата z = 0. Это равенство и будет уравнением координатной плоскости х0у. Аналогично получаем уравнения других координатных плоскостей (рис. 15).

Рис. 15. Графическое представление координатных плоскостей:

z = 0 — уравнение плоскости х0у,

у = 0 — уравнение плоскости х0z,

х = 0 — уравнение плоскости y0z.

Для вывода уравнения поверхности обычно используют то свойство, которым обладают все точки поверхности.

Например, для сферы — множества точек М(x, y, z) пространства, удалённых от точки (центра) О₀(x₀, y₀, z₀) на расстояние R, — можем получить [2, гл. IV, п. 12.1] уравнение

(х – х₀)² + (у – у₀)² + (z – z₀)² = R². (24)

Разумеется, если имеем уже известное уравнение, то сможем построить соответствующую ему поверхность.

Пример 17 [1, к задачам № 51-60, п. d].

Дано уравнение х² + у² + z² – 4z = 0.

Установить, какую поверхность в пространстве оно определяет и сделать схематический рисунок.

Решение

Приведём это уравнение к виду (24). Как и в примере 16, п. 3, выделим полный квадрат в слагаемых, содержащих переменную z. В результате получим уравнение, которое является частным случаем уравнения (24).

х² + у² + (z – 2)² = 4.

Это означает, что данное уравнение определяет сферу с центром в точке О₀(0; 0; 2) и радиусом R = 2 (рис. 16).

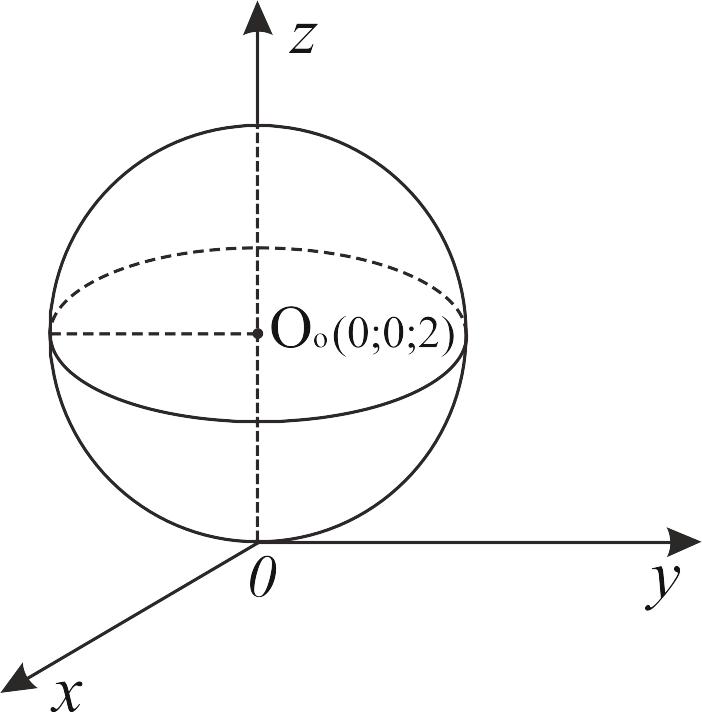
Рис. 16. Изображение сферы х² + у² + z² – 4z = 0