3.3. Понятие уравнения линии на плоскости

В аналитической геометрии на плоскости, говоря о «точке», мы подразумеваем «пару чисел» и наоборот. Аналогичная картина наблюдается при изучении линий. Здесь: «линия» ↔ «уравнение». Такое соответствие между геометрическими и алгебраическими объектами позволяет использовать в геометрии законы алгебры и анализа. Пусть на плоскости задана линия  и введена прямоугольная система координат х0у (рис. 4).

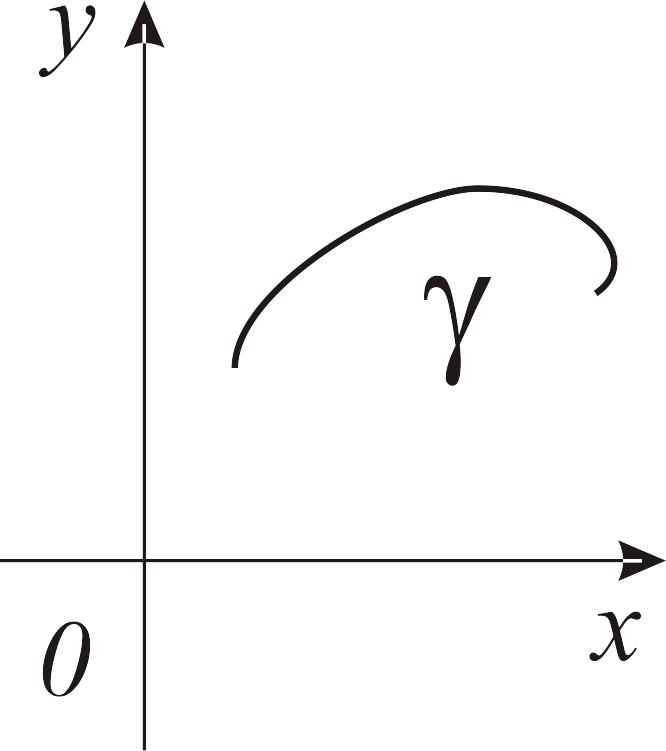
Рис. 4. Изображение линии и системы координат х0у

Уравнением линии  относительно прямоугольной системы координат называют уравнение

F(х, у) = 0,

которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты точек, не лежащих на ней.

Примечание. Аналогично определяется уравнение линии  относительно любой другой системы координат, например полярной.

Для составления уравнения линии обычно используют то свойство, которым обладают все точки линии.

Но линию на плоскости можно рассматривать не только как множество точек, обладающих заданным свойством, а ещё и как траекторию движущейся точки М(х; у). Тогда её можно описать с помощью системы уравнений, определяющих положение точки М в зависимости от некоторого параметра t:

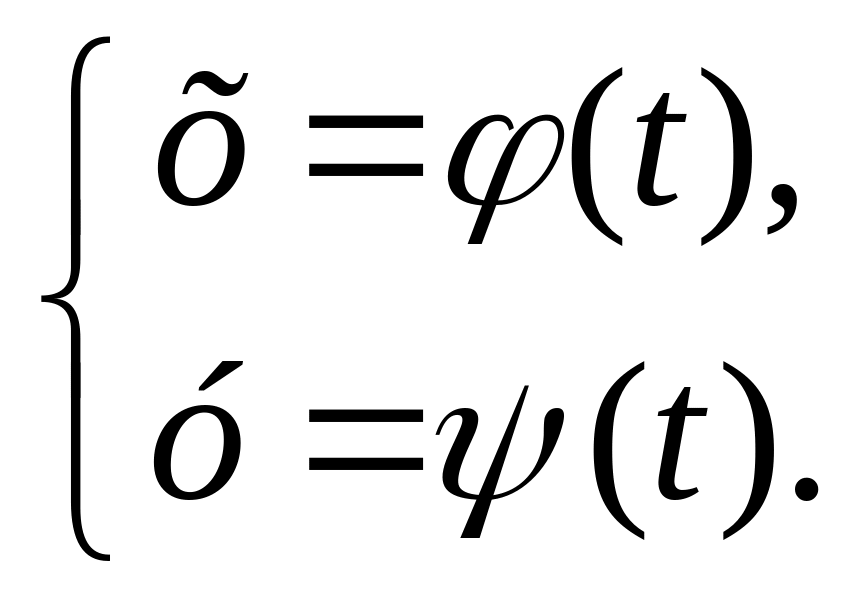
Эти два уравнения называют параметрическими уравнениями линии , а t — параметром.

Пример 12. Точка М(х; у) движется на одинаковом удалении R от начала координат с постоянной угловой скоростью . Описать траекторию движения точки с помощью уравнений.

Решение

Очевидно, траекторией движения точки будет окружность (рис. 5) с радиусом R и центром в начале координат.

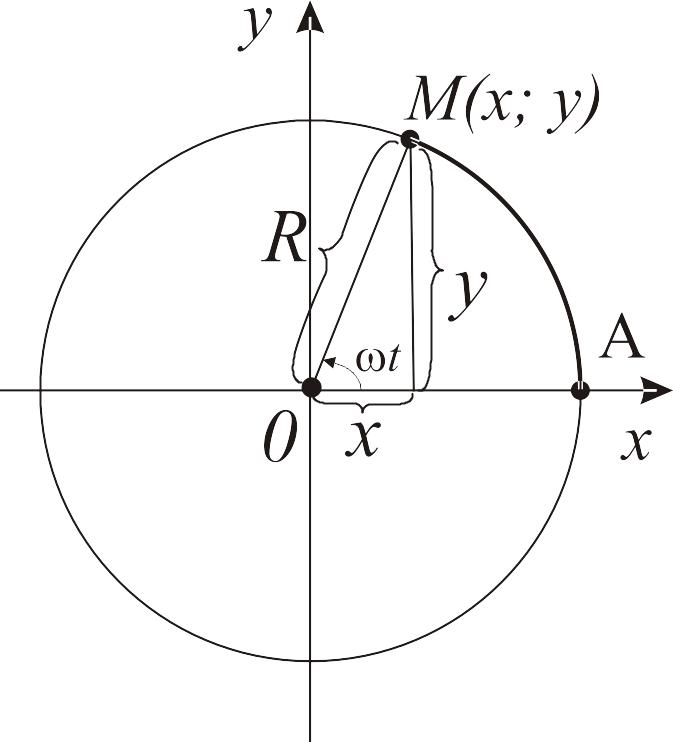
Рис. 5. Изображение траектории движения точки М из начального положения (точка А)

За параметр t возьмём время движения точки М из начального положения А. Тогда ^ и параметрическими уравнениями окружности будут

.

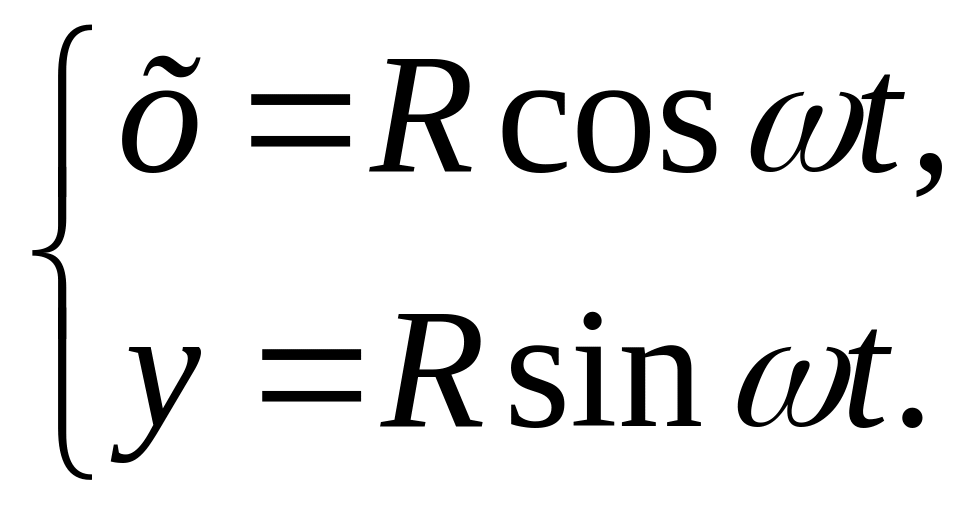Если же эту окружность рассматривать как множество точек плоскости, удалённых от точки 0 на расстояние R, то получим её уравнение (например, по теореме Пифагора) в прямоугольных координатах

Из определения уравнения линии вытекают следующие утверждения:

1)

2) координаты точек пересечения линий, заданных уравнениями F₁(x, y) = 0 и F₂(x, y) = 0, находят из системы уравнений

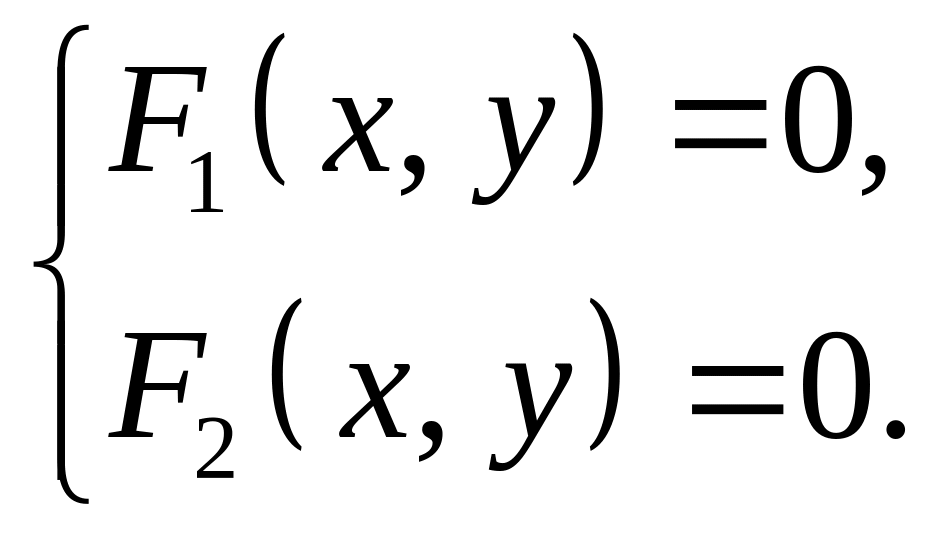
Пример 13. Даны уравнения линий ₁ и ₂:

, .

Требуется:

1) найти точки пересечения линий;

2) проверить, лежит ли точка Q(1; 2) на линиях ₁ и ₂.

Решение

1. Точки пересечения линий ₁ и ₂ найдём, решая систему

Выражая из второго уравнения y = 2x и подставляя в первое, получим

Тогда у₁ = 0, у₂ = 4. Следовательно, точками пересечения линий ₁ и ₂ будут точки Р₁(0; 0) и Р₂(2; 4).

2. Проверим, лежит ли точка Q(1; 2) на линии ₁. Для этого подставим её координаты в уравнение этой линии:

1² + 2² – 6 · 1 – 2 · 2 = –5 ≠ 0.

Следовательно, Q  ₁. Аналогично делаем проверку принадлежности точки Q линии ₂:

2  1 – 2 = 0.

Значит, Q  ₂.

3.4. Уравнения прямой линии на плоскости

Изобразим прямую  в прямоугольной системе координат (рис. 6).

Рис. 6. Прямая линия

 — прямая линия; b — отрезок, отсекаемый прямой  по 0y; α — угол наклона прямой  (0 ≤ α ≤ π); tg α = k — угловой коэффициент прямой , где .

Наиболее важными уравнениями прямой на плоскости являются:

1) уравнение прямой с угловым коэффициентом k и отрезком в:

y = kx + в;

2) уравнение прямой, перпендикулярной оси 0x:

x = a;

3) уравнение прямой, параллельной оси 0х:

у = в;

4) уравнение прямой, проходящей через заданную точку М₁(х₁; у₁) с угловым коэффициентом k:

y – y₁ = k (х – х₁); (14)

5) уравнение прямой, проходящей через две точки М₁ (х₁; у₁) и М₂(х₂; у₂):

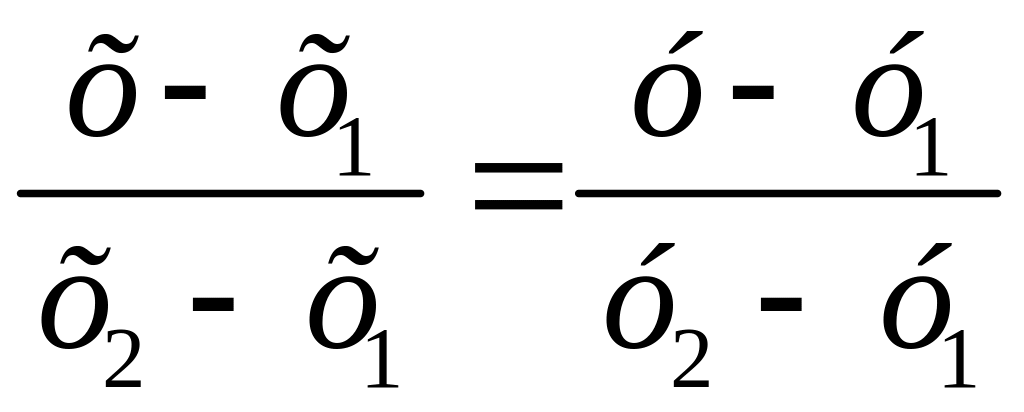, (15)

где х₁  х₂, y₁  y₂.

Все эти уравнения — частные случаи уравнения прямой общего вида

Ах + Ву + С = 0 (16)

Замечание. Для прямой общего вида угловой коэффициент определяется по формуле

, (17)

а для прямой, проходящей через две точки М₁(х₁; у₁) и М₂(х₂; у₂), — по формуле

. (18)

Пример 14 [1, к задачам № 31-40, п. 1, 2]. Даны вершины треугольника: А(1; 2), В(–1; –3) и С(5; –7).

Требуется:

1) написать уравнение и найти угловой коэффициент прямой АВ;

2) найти угловой коэффициент прямой ВС;

3) написать уравнение медианы АD.

Решение

1) Уравнение прямой АВ напишем как уравнение прямой, проходящей через две точки. За первую точку возьмём точку А, а за вторую — точку В. Тогда х₁ = 1, у₁ = 2; х₂ = –1; у₂ = –3.

По формуле (15) получим

или

5x-2y-1=0 — уравнение АВ.

Угловой коэффициент прямой АВ находим по формуле (17):

.

2) Для того чтобы найти угловой коэффициент прямой ВС, необязательно выводить её уравнение. Можно сразу воспользоваться формулой (18).

Взяв за первую точку — точку В, а за вторую — точку С, получим

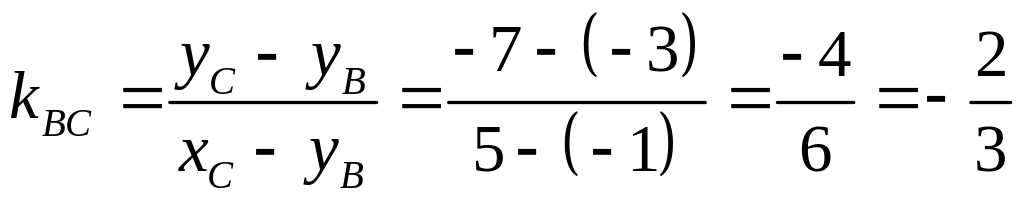, т.е .

3) Для того чтобы написать уравнение медианы АD, найдём сначала координаты точки D. Точка D делит отрезок ВС пополам. По формулам (13) получаем

, ,

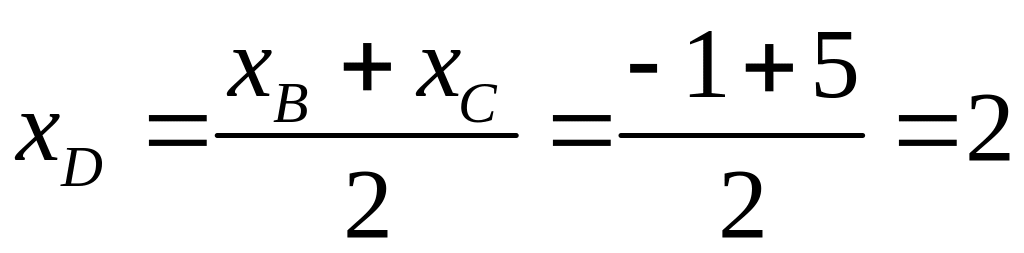т.е. D(2; –5).

Остаётся воспользоваться уравнением (15), как это было сделано в п. 1. В результате получим уравнение медианы АD

, .