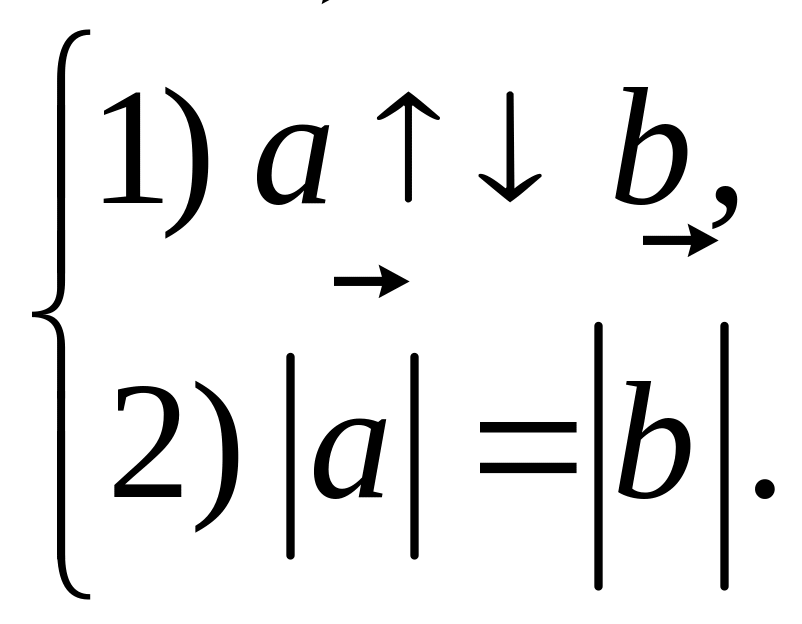1.2. Понятие определителя

Определитель вводят для квадратных матриц. Порядок определителя совпадает с порядком матрицы. Определитель матрицы А обозначают А, det A, Δ, …

Для матрицы первого порядка А = (а₁₁) определитель (первого порядка) равен А = а₁₁.

Для матрицы второго порядка определитель (второго порядка) равен

Для матрицы третьего порядка определитель (третьего порядка) равен

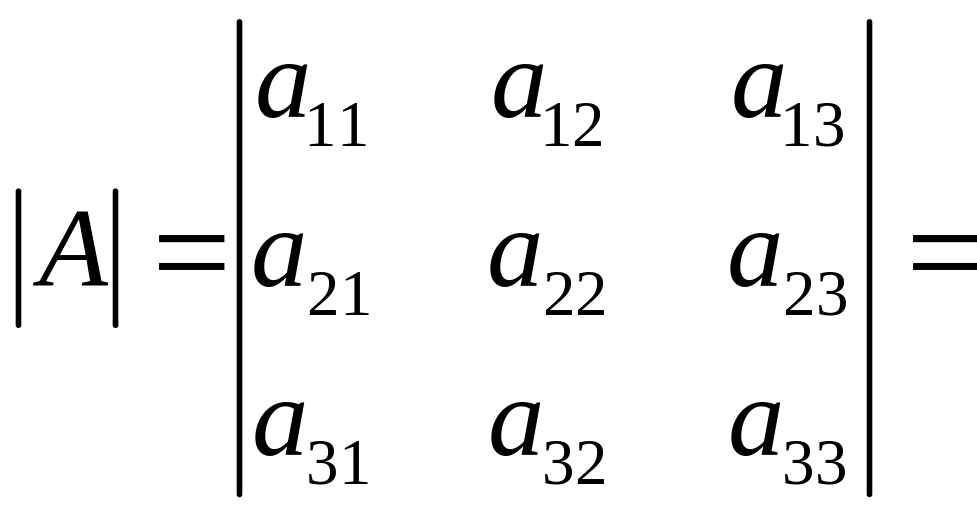
(2)

Это правило называют правилом треугольников или правилом Саррюса. Его можно изобразить схематически следующим образом:

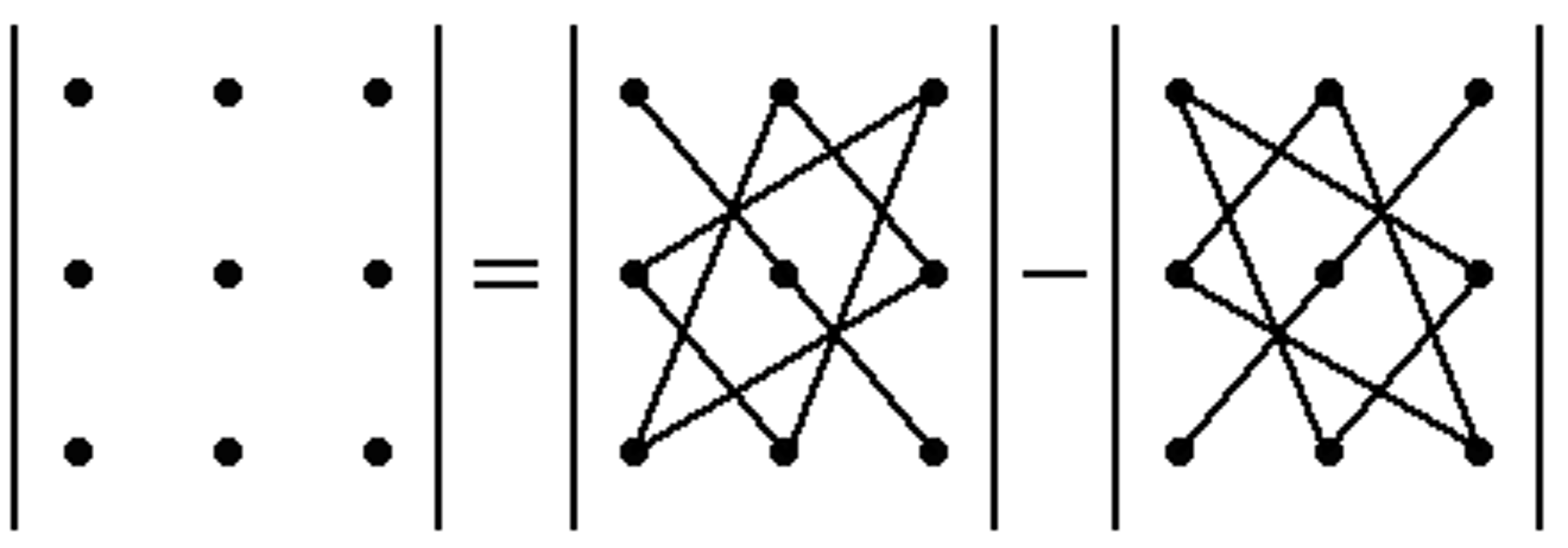
Пример 3. Вычислим по правилу (2) определитель:

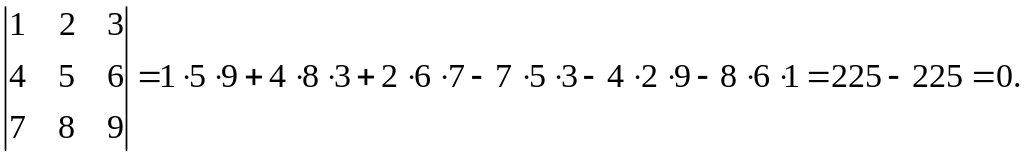
Кроме правила треугольников, в практике используют еще один простой способ вычисления определителей, который вытекает из теоремы Лапласа. Этим способом можно вычислять определители любого порядка. Для этого способа нам потребуются минор и алгебраическое дополнение элемента.

Определение 3. Минором М_ik элемента a_ik определителя любого порядка называют новый определитель, который получается из данного после вычеркивания i-й строки и k-го столбца. Например, для определителя

(3)

минорами элементов а₁₁, а₁₂, … будут соответственно определители

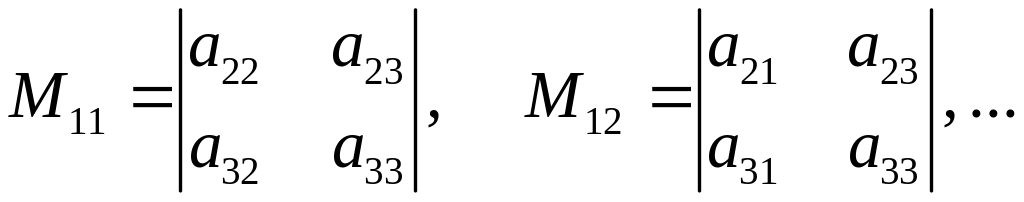
Очевидно, что порядок минора на единицу меньше порядка исходного определителя.

Определение 4. Алгебраическим дополнением А_ik элемента а_ik определителя называют

A_ik = (–1)^{i + k}M_ik.

Например, для определителя Δ из (3)

А₁₁ = (–1)^{1 + 1}М₁₁ = М₁₁, А₁₂ = (–1)^{1 + 2}М₁₂ = –М₁₂.

Теорема Лапласа. Сумма произведений элементов какой-либо строки или столбца определителя  на соответствующие алгебраические дополнения равна определителю .

Эту теорему используют для вычисления определителей. Например, выбрав в определителе (3) первую строку, получим

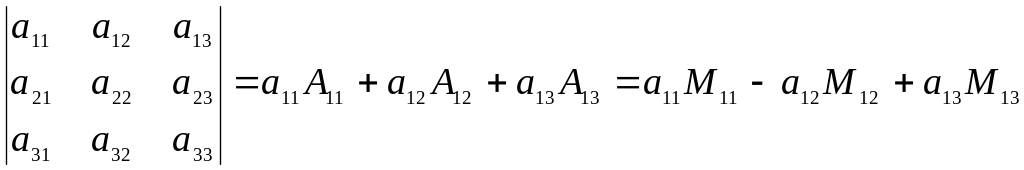. (4)

Формулу (4) называют разложением определителя по элементам первой строки. Вместо первой строки можно брать любую другую строку или любой столбец определителя.

Пример 4. Вычислим определитель из примера 3 по формуле (4).

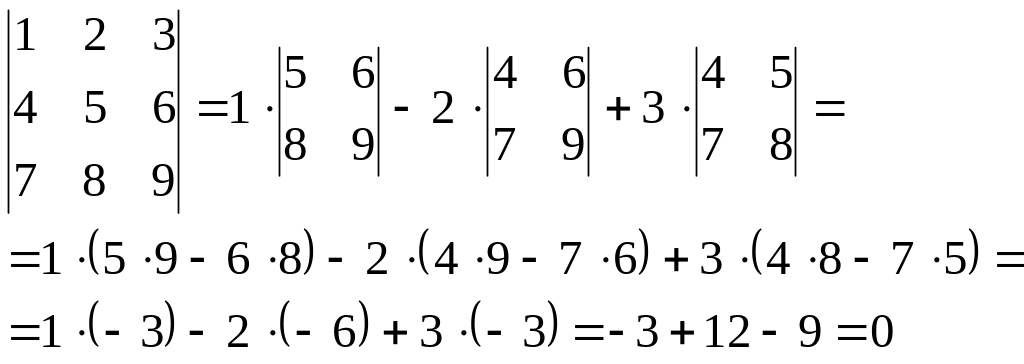
Результат, разумеется, тот же, что и в примере 3.

Замечание. При вычислении определителя с помощью теоремы Лапласа обычно выбирают ту строку или столбец, где имеются нули. При этом нули можно получать искусственно с помощью свойств определителей [2, гл. I, п. 2.2].

1.3. Решение систем линейных уравнений

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

(5)

Решением системы (5) называют упорядоченную тройку чисел x = α, y = β, z = γ, удовлетворяющих всем уравнениям системы. Система (5) может не иметь решений, может иметь одно или бесконечное множество решений. Существует достаточное число способов отыскания решений системы (5). Мы рассмотрим два из них: метод Крамера и метод Гаусса. Для метода Крамера надо ввести главный определитель системы. Он имеет вид (3). Если Δ ≠ 0, то система (5) имеет единственное решение, которое определяется по формулам Крамера:

(6)

где

(7)

Пример 5 [1, к задачам № 11-20]. Решить по формулам Крамера систему линейных уравнений.

(8)

Решение

Вычислим главный определитель системы

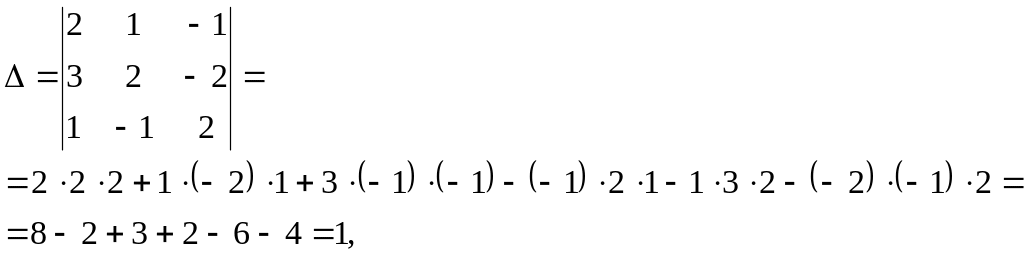
т.к. Δ ≠ 0, то система имеет единственное решение.

Вычислим определители Δ_x, Δ_y, Δ_z по формулам (7):

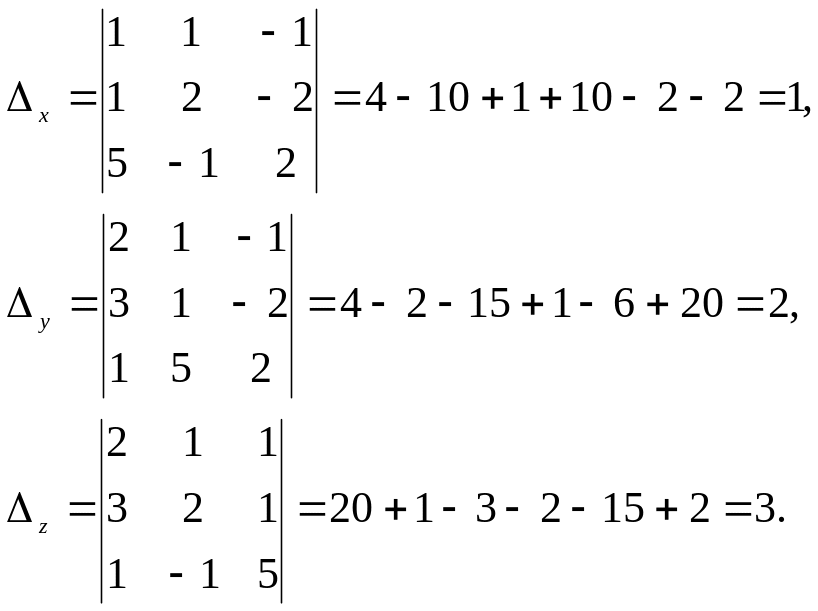
По формулам Крамера (6) находим:

Ответ: x = 1; y = 2; z = 3.

Рассмотрим теперь метод последовательного исключения неизвестных, или метод Гаусса [2, гл. I, п. 4.4]. Исключение неизвестных осуществляется с помощью равносильных действий над уравнениями системы. Этим методом система (5) преобразуется в равносильную систему треугольного вида:

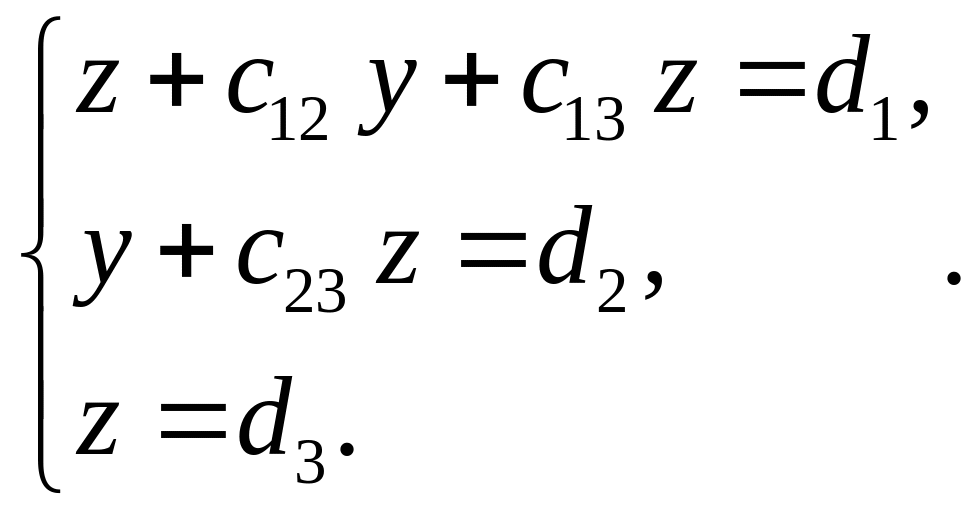
После этого из третьего уравнения находим z, из второго — y, из первого — x.

Пример 6. Решить методом Гаусса систему уравнений (8).

Решение

Поменяем местами первое и третье уравнения:

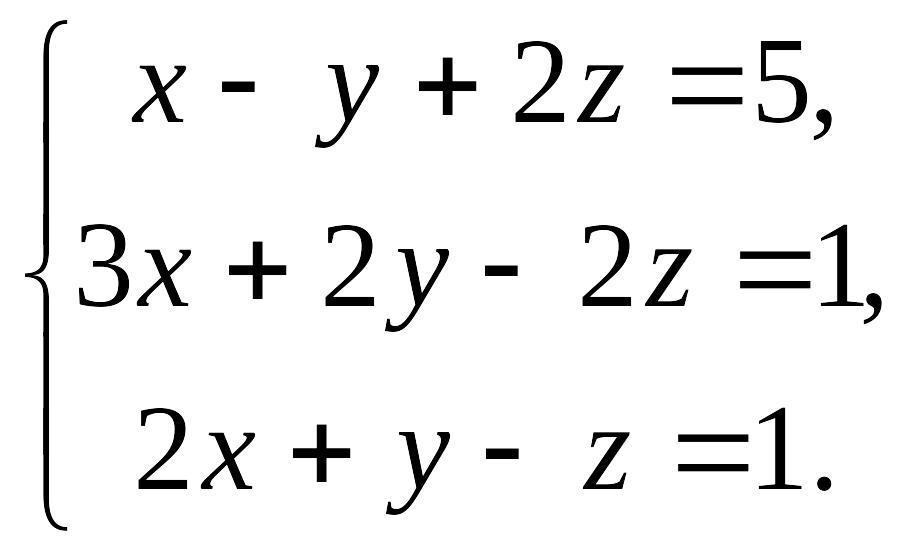
Умножим все члены первого уравнения системы на (–3) и прибавим ко второму, получим систему

Теперь умножим все члены первого уравнения на (–2) и прибавим к третьему, получим систему

Разделим все члены второго уравнения на 5 (коэффициент при y):

Умножим второе уравнение на (–3) и прибавим к третьему уравнению. Тогда получим систему

из которой последовательно находим

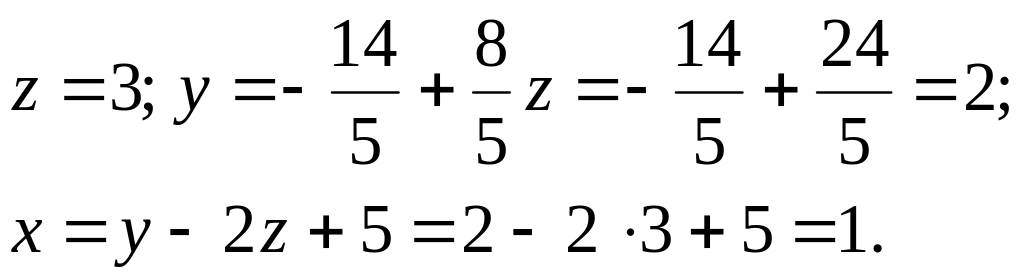
Ответ: x = 1, y = 2, z = 3.

Как видим, оба метода дают один и тот же результат.

Замечание. Методом Гаусса можно решать линейную систему при любом числе уравнений, а также и в случае, когда ее определитель равен нулю и когда число уравнений не совпадает с числом неизвестных.

Контрольные вопросы

1. Матрицы и их виды.

2. Действия над матрицами.

3. Определители второго и третьего порядков, их свойства.

4. Понятие минора и алгебраического дополнения. Разложение определителя по элементам строки или столбца.

5. Общие сведения о системах линейных уравнений.

6. Методы решения систем линейных уравнений.

2. Элементы векторной алгебры

В векторной алгебре [2, гл. II] выделяют три наиболее важных вопроса:

1) понятие и виды векторов;

2) действия над векторами;

3) применения векторов.

Для удобства представим необходимые сведения по этим вопросам в виде таблиц 1-3.

2.1. Понятие вектора, виды векторов

Таблица 1

Основные определения

Название	Определение	Обозначение
1	2	3
1. Вектор	Направленный отрезок от точки А до точки В
2. Длина (модуль) вектора	Длина отрезка
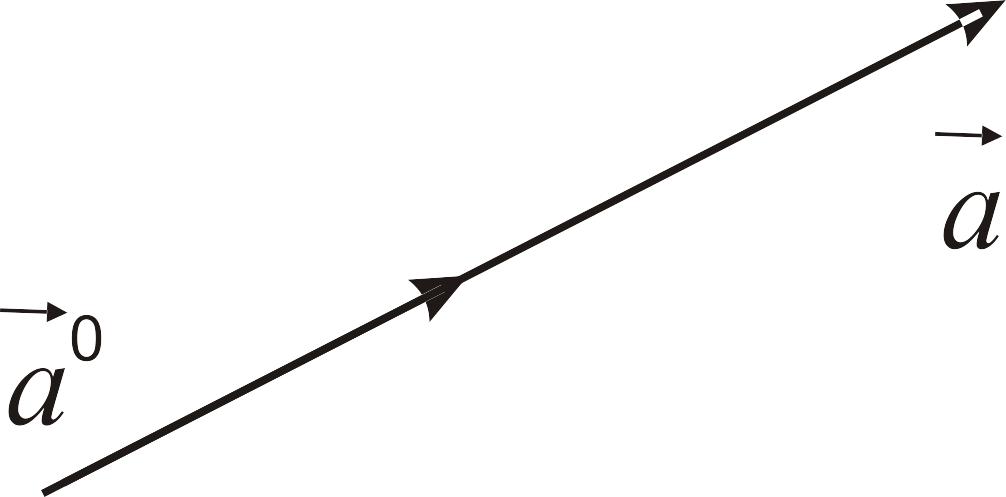
3. Орт данного направления
4. Нулевой вектор	Начало совпадает с концом (точка)
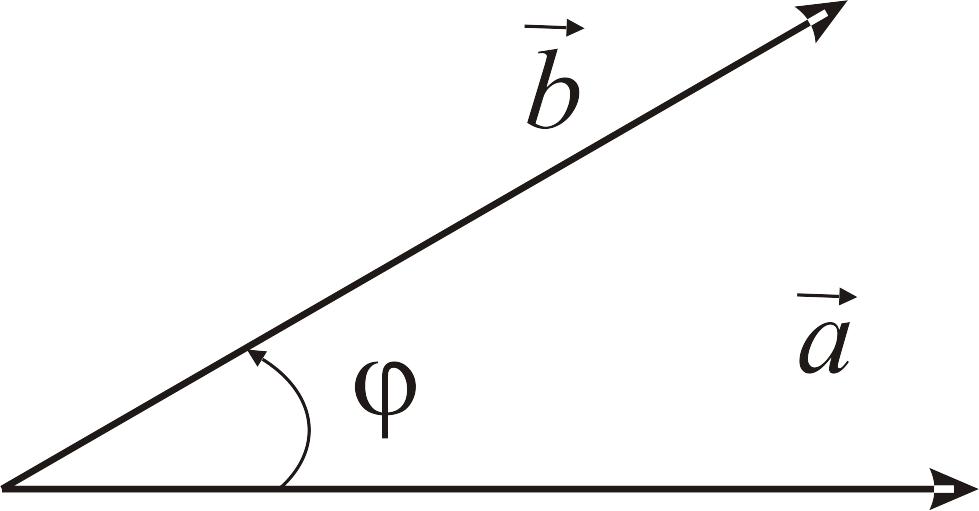
5. Угол между векторами
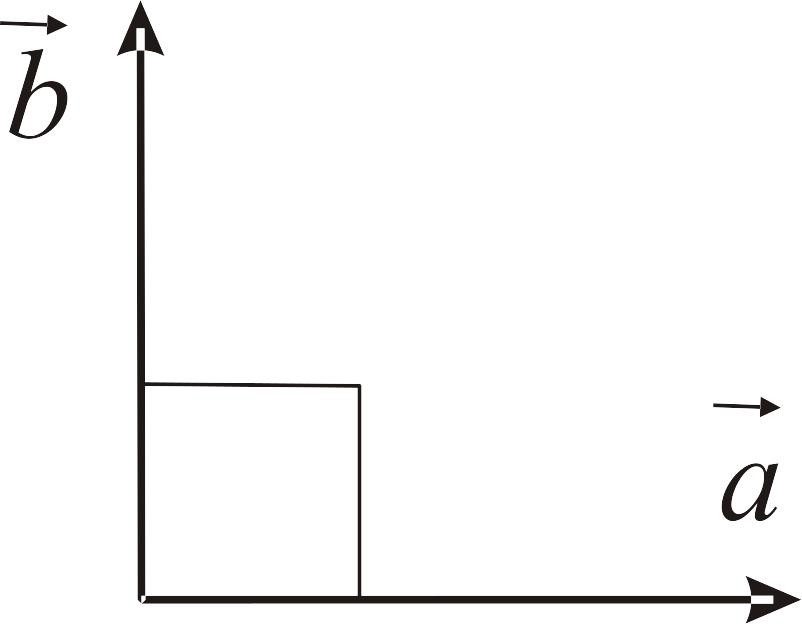
6. Перпендикулярные векторы

Продолжение таблицы 1

1	2	3
7. Коллинеарные векторы	Лежат на одной или на параллельных прямых	||
8. Сонаправленные векторы	Коллинеарны и имеют одинаковое направление
9. Антинаправленные векторы	Коллинеарны и направлены в противоположные стороны
10. Равные векторы
11. Противоположные векторы
12. Компланарные векторы	Лежат в одной или нескольких параллельных плоскостях
13. Правая тройка некомпланарных векторов	1) начала векторов совмещены; 2) кратчайший поворот от к виден из конца совершающимся в положительном направлении
Примечание. Если кратчайший поворот от к виден из конца совершающимся в отрицательном направлении, т.е. по движению часовой стрелки, то тройку векторов называют левой.