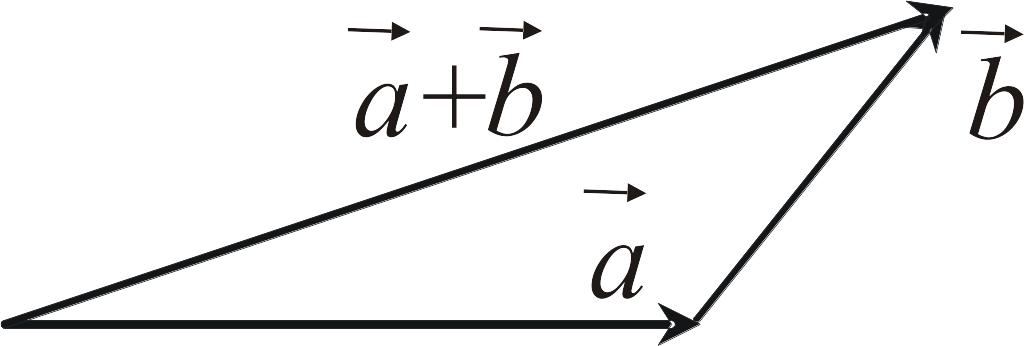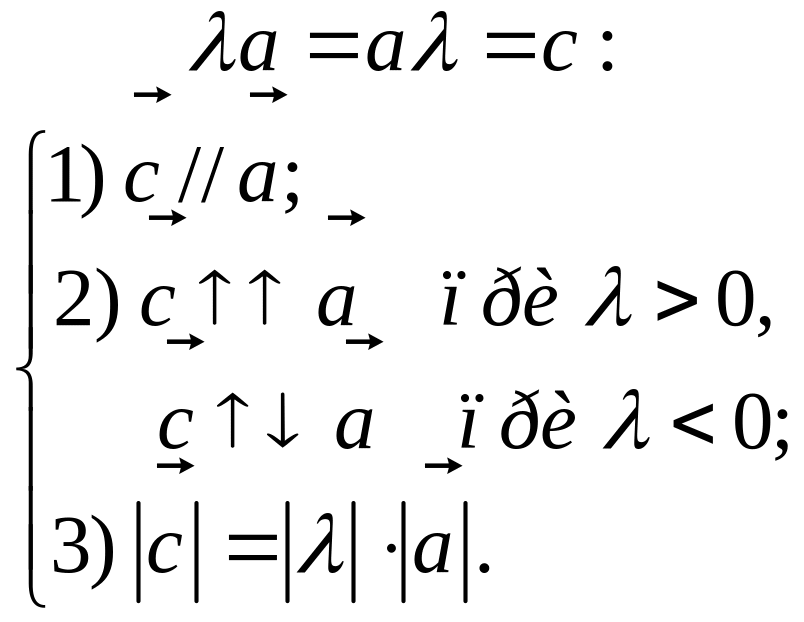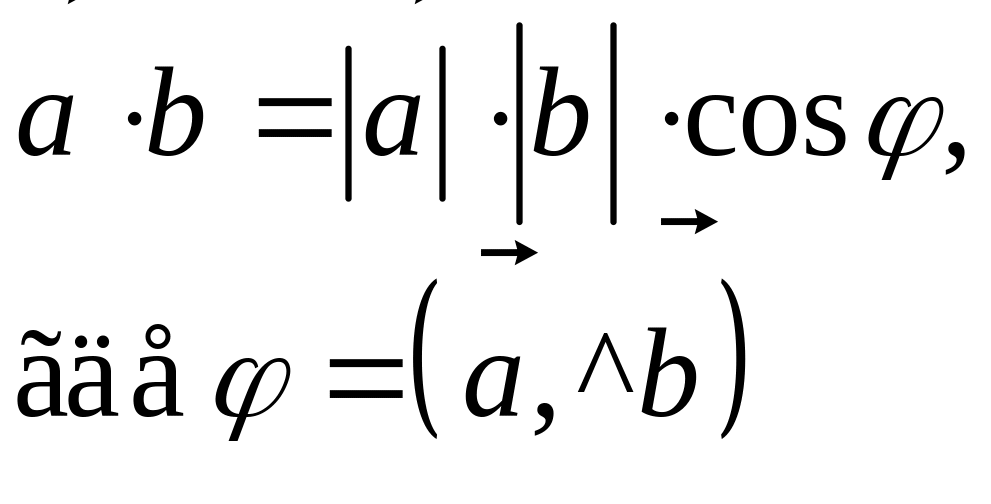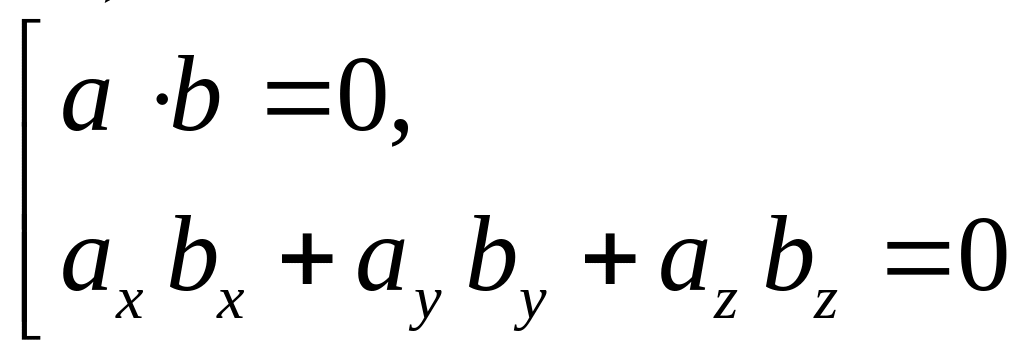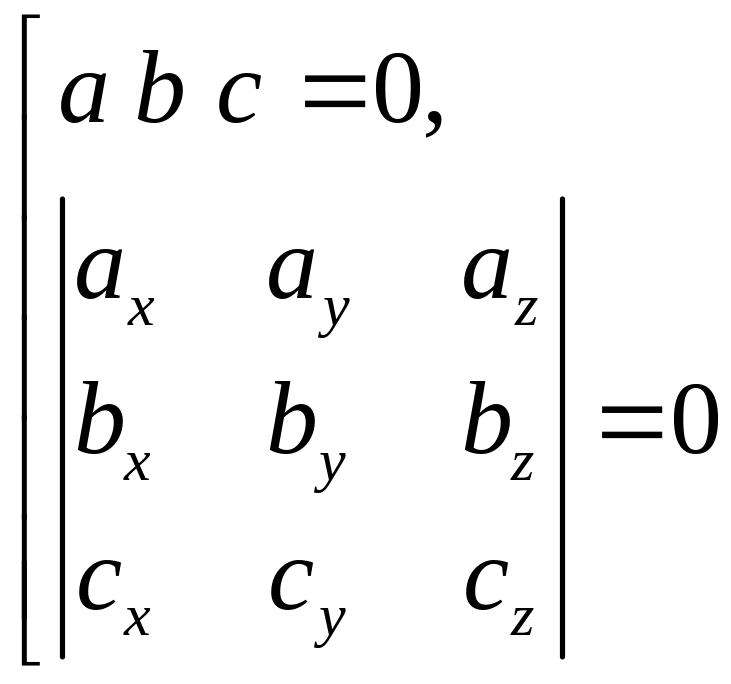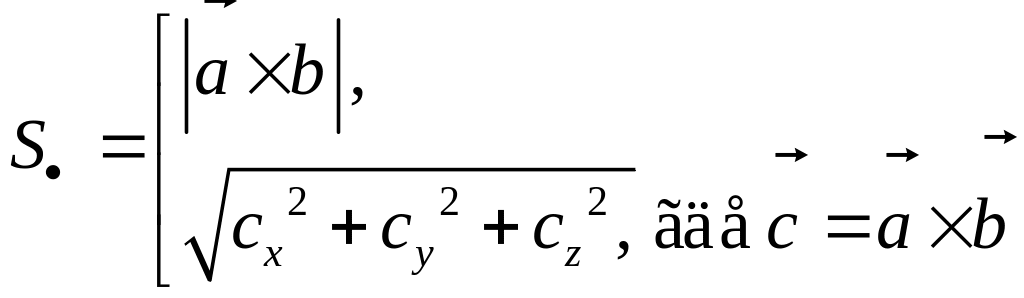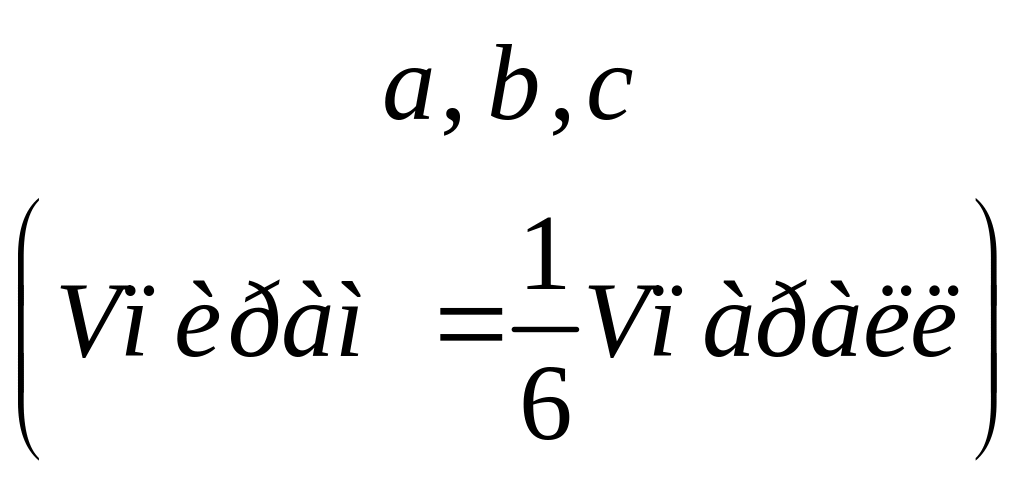- •Оглавление
- •Введение
- •1. Элементы линейной алгебры
- •1.1. Понятие матрицы. Действия над матрицами
- •1.2. Понятие определителя
- •1.3. Решение систем линейных уравнений
- •2.2. Действия над векторами
- •2.3. Применения векторов
- •3. Аналитическая геометрия
- •3.1. Системы координат
- •3.2. Простейшие задачи на метод координат
- •3.3. Понятие уравнения линии на плоскости
- •3.4. Уравнения прямой линии на плоскости
- •3.5. Задачи на прямую на плоскости
- •3.6. Кривые второго порядка
- •3.7. Примеры на построение линий по их уравнениям
- •3.8. Понятие уравнения поверхности в пространстве
- •3.9. Плоскость
- •3.10. Цилиндрические поверхности
- •3.11. Поверхности второго порядка
- •3.12. Уравнения линии в пространстве
- •Список рекомендуемых источников
2.2. Действия над векторами
В предыдущем параграфе мы определили вектор как направленный отрезок. Однако вектор можно определять еще и с помощью координат. Это позволяет использовать в векторной алгебре законы алгебры и анализа. Координатами вектора называют проекции вектора на координатные оси [2, гл. II, п. 5.3, 5.4]. Вектор, имеющий координаты аx, аy, аz, можно записывать в двух равнозначных формах:
![]()
или
![]() (9)
(9)
Выражение
(9) называют разложением вектора
![]() по базисным векторам (
по базисным векторам (![]() —
единичные взаимно перпендикулярные
векторы
— базис в пространстве;
—
единичные взаимно перпендикулярные
векторы
— базис в пространстве;
![]() — базис на плоскости).
— базис на плоскости).
Замечание. Если
начало вектора находится в точке М1
(x1;
y1;
z1),
а конец в точке М2
(x2;
y2;
z2),
то вектор
![]() будет
иметь координаты
будет
иметь координаты
![]() . (10)
. (10)
Пример
7
[1, к задачам № 21-30, п. 1]. Даны
точки А(1;
6; 5) и В(3;
4; 5).
Найти
координаты вектора
![]() .
.
Решение
Принимая за начало
вектора
точку А, а за конец — точку В, по формуле
(10) получим
![]()
Замечание. В координатной форме векторы считаются равными, если равны их соответствующие координаты, т.е.

Рассмотрим теперь, какие действия производятся над векторами и как они осуществляются. Следует только помнить, что эти действия можно выполнять как в векторной, так и в координатной формах. Все действия над векторами приведены в таблице 2.
Таблица 2
Действия над векторами
Название |
Определение в векторной форме |
Выражение в координатной форме |
1. Сложение векторов |
1) по правилу параллелограмма |
|
|
||
2) по правилу треугольника |
||
|
||
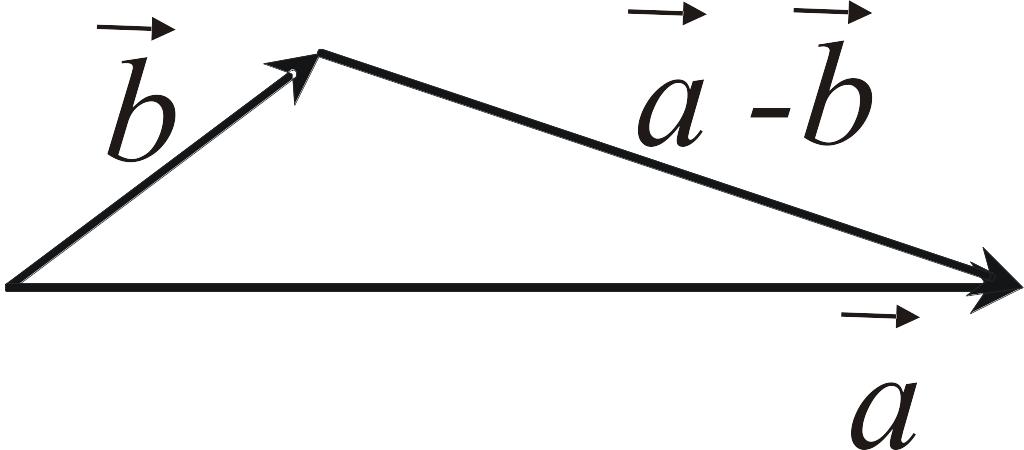
2. Вычитание векторов |
Как действие, обратное сложению:
|
|
|
||
3. Умножение вектора на число λ |
|
|
4. Скалярное
произведение векторов
|
|
|
5. Векторное произведение векторов |
|
|
6. Смешанное
произведение векторов
|
|
|
Пример 8 [1, к задачам № 21-30]. Даны векторы:
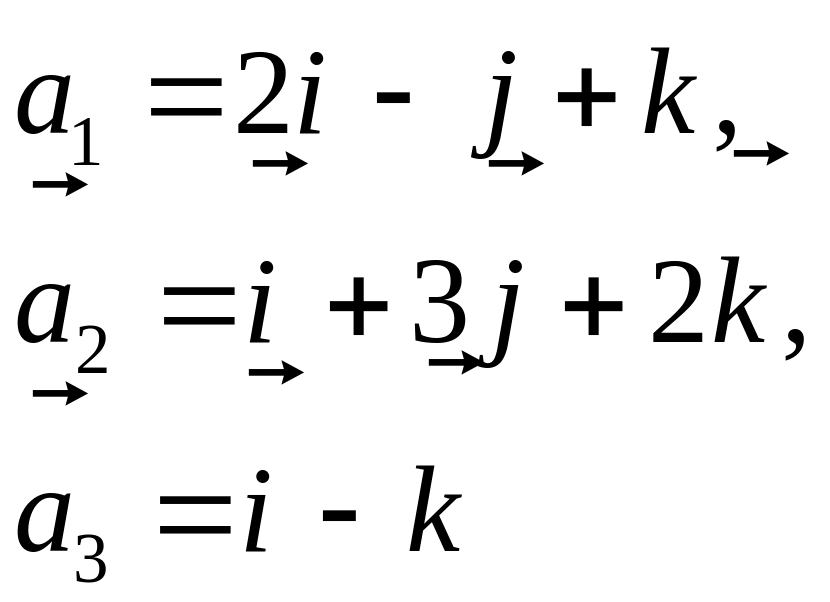
Найти:
![]()
Решение
Векторы
![]() заданы в виде разложений по базисным
векторам. Найдем их координаты:
заданы в виде разложений по базисным
векторам. Найдем их координаты:
![]()
Выполним вышеуказанные действия над векторами, учитывая, что векторы заданы координатами. Используя таблицу 2, получим:

2.3. Применения векторов
Рассмотренные операции над векторами, а также получающиеся из них следствия широко используют в практике (табл. 3).
Таблица 3
Основные применения векторов
Словесное название |
Выражение в
|
1 |
2 |
1. Длина вектора
— длина отрезка
|
|
2. Единичный
вектор
|
|
3. Угол
|
|
4. Условие
|
|
5. Условие
|
|
6. Условие компланарности векторов
|
|
Продолжение таблицы 3
1 |
2 |
7. Площадь параллелограмма S, построенного на векторах
(SΔ
=
|
|
8. Объем
параллелепипеда Vпаралл,
построенного
на векторах
|
|
Пример 9 [1, к задачам № 21-30]. Даны координаты вершин пирамиды ДАВС: А (1; 2; –1), В (0; 1; 5), С (–1; 2; 1), Д (0; 1; 6). Средствами векторной алгебры найти:
1) координаты
векторов
![]()
2) длину вектора
![]()
3) площадь грани АВС;
4) объем пирамиды ДАВС.
Решение
1. Сначала найдем координаты векторов . Как и в примере 7, по формуле (10) получим:
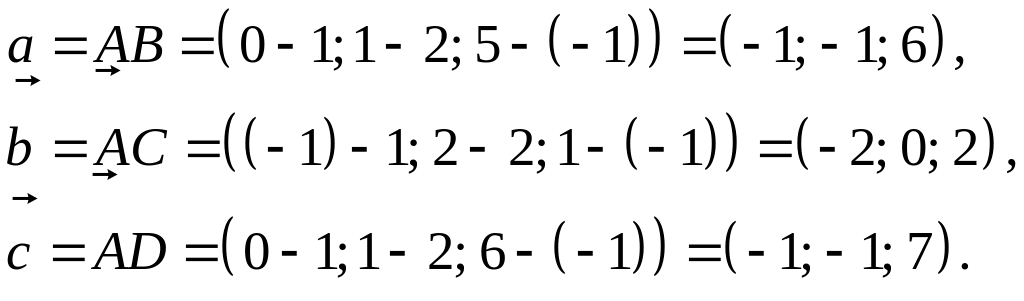
2. Найдем теперь
координаты вектора
![]() Для этого воспользуемся 1, 2, 3 пунктами
таблицы 2. Тогда получим:
Для этого воспользуемся 1, 2, 3 пунктами
таблицы 2. Тогда получим:

Для определения
длины вектора
![]() можно воспользоваться результатом
пункта 1 из таблицы 3:
можно воспользоваться результатом
пункта 1 из таблицы 3:
![]()
3. Угол между
векторами
![]() найдем, используя п. 3 табл.
3:
найдем, используя п. 3 табл.
3:
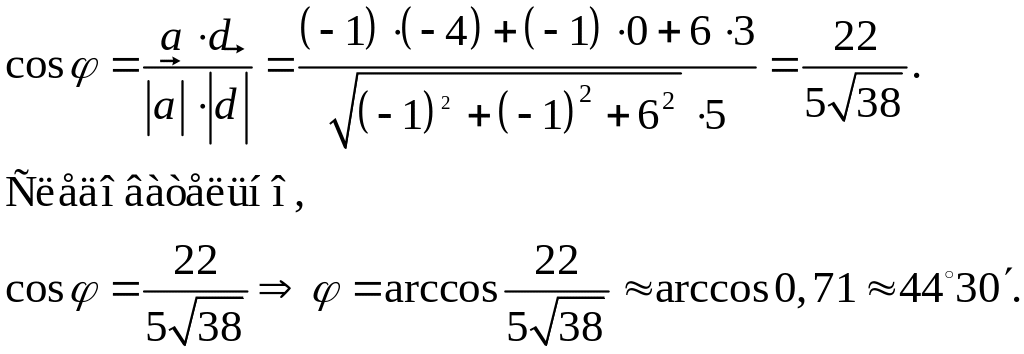
4. Площадь грани АВС (см. п. 7, табл. 3,) равна:
![]()
Так как
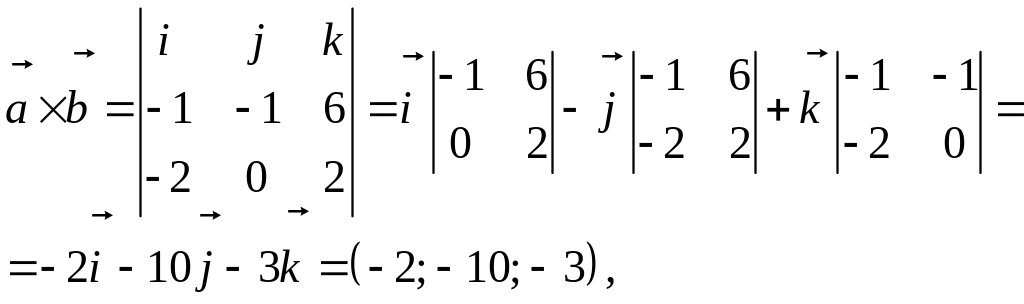
то с учетом п. 1 табл. 3 получим
![]()
А площадь грани
![]() (ед.2).
(ед.2).
5. Объем пирамиды ДАВС (см. п. 8 табл. 3) равен
![]()
Найдем смешанное произведение (см. п. 8 табл. 2):
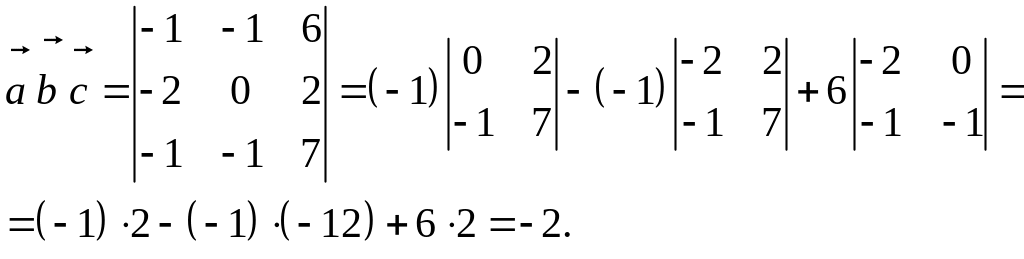
Объем пирамиды
![]() .
.
Контрольные вопросы
1. Дайте понятие базиса на плоскости и в пространстве.
2. Дайте понятие координат вектора на плоскости и в пространстве.
3. Что такое скалярное произведение векторов? Где оно применяется?
4. Дайте определение векторного произведения векторов и укажите, где его применяют.
5. Дайте определение смешанного произведения векторов и укажите, где его применяют.