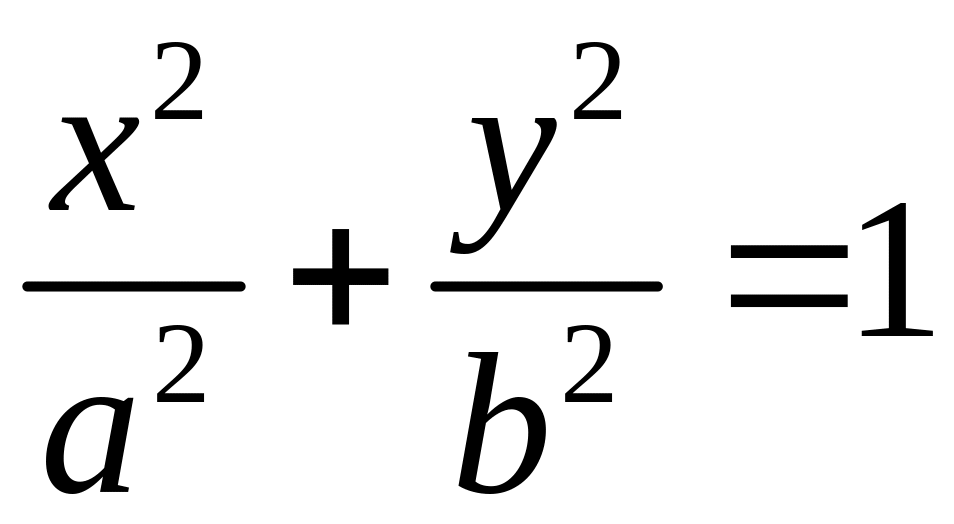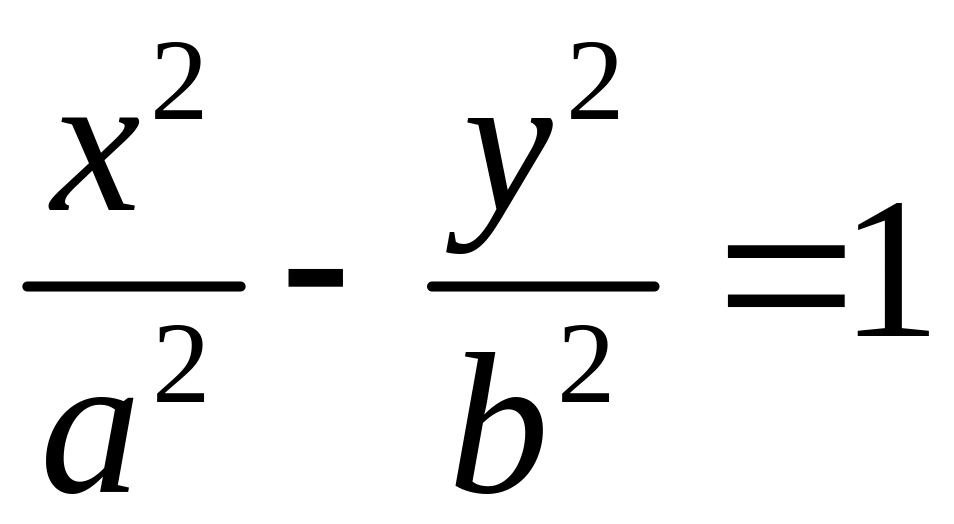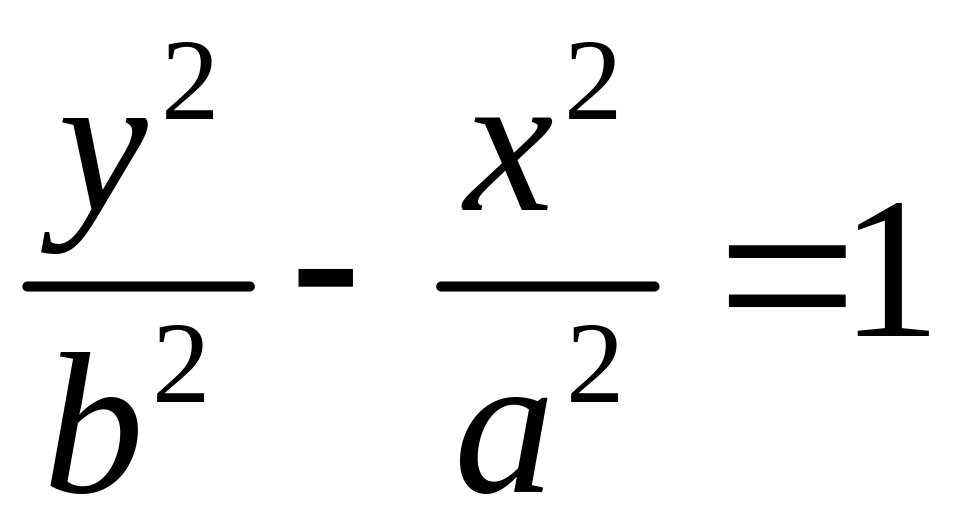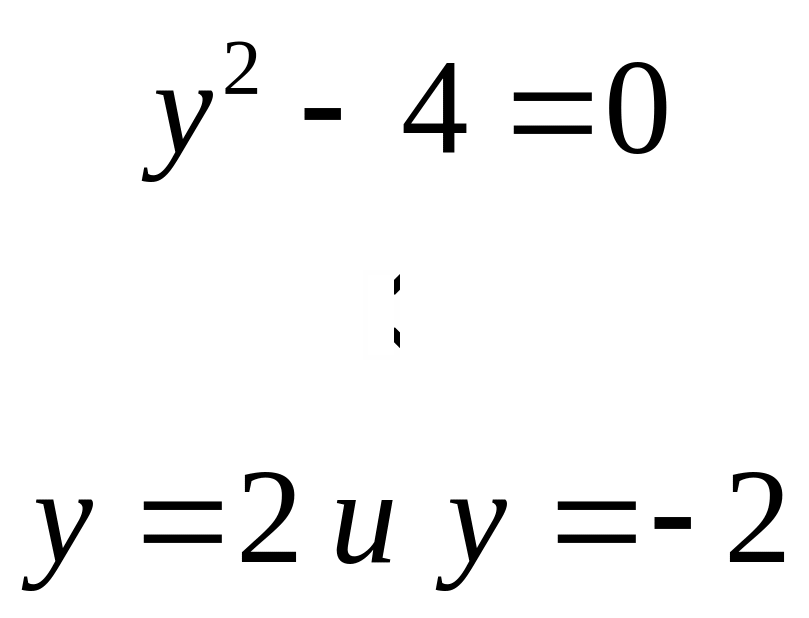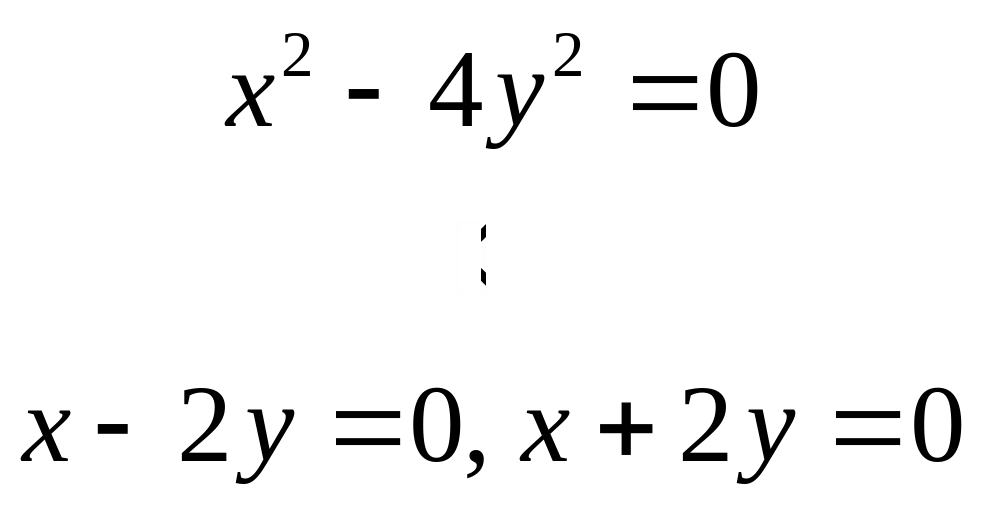3.5. Задачи на прямую на плоскости

Для прямых ₁ и ₂, заданных уравнениями

; ,

имеем:

1) — условие параллельности ₁ || ₂;

2) — условие перпендикулярности ₁  ₂;

3) , (19)

где угол  между ₁ и ₂ отсчитывают от ₁ до ₂ в положительном направлении (т.е. против движения часовой стрелки).

Если надо найти острый угол между двумя прямыми, то используют формулу

.

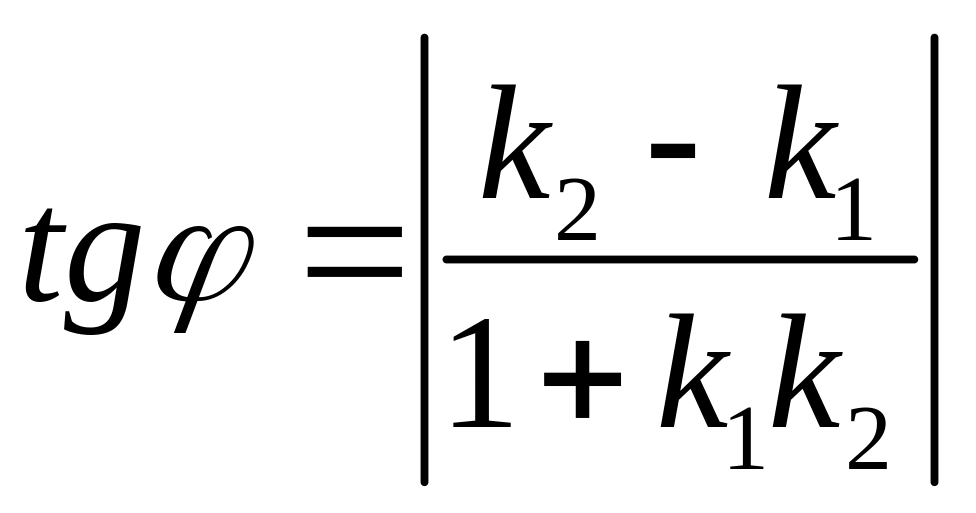4) Для определения расстояния от точки М₀(х₀; у₀) до прямой, заданной общим уравнением (16), используют формулу

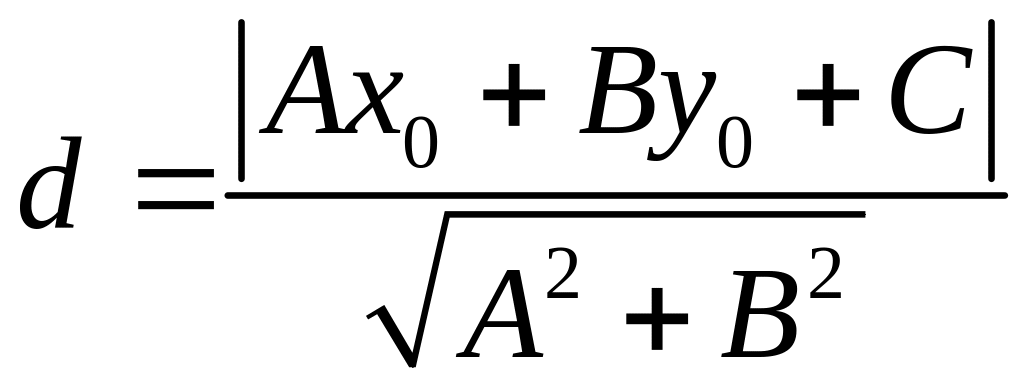. (20)

Пример 15 [1, к задачам № 31-40, п. 3, 4]. Даны вершины треугольника: А(–1; 0), В(2; 4) и С(3; 1).

Требуется:

1) написать уравнение высоты СD;

2) найти внутренний угол А;

3) найти длину высоты СD.

Решение

Для решения задачи сделаем схематический рисунок (рис. 7).

1) Сначала найдём угловой коэффициент прямой СD. Так как СD  АВ, то . Угловой коэффициент k_АВ найдём по формуле (18). За первую точку берём точку А, за вторую — точку В.

В результате получим

.

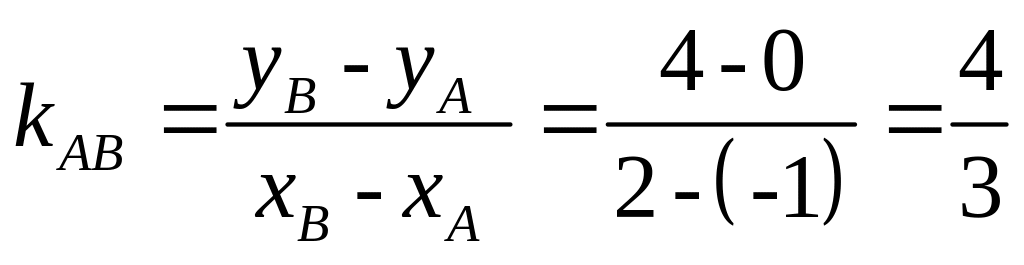Но тогда .

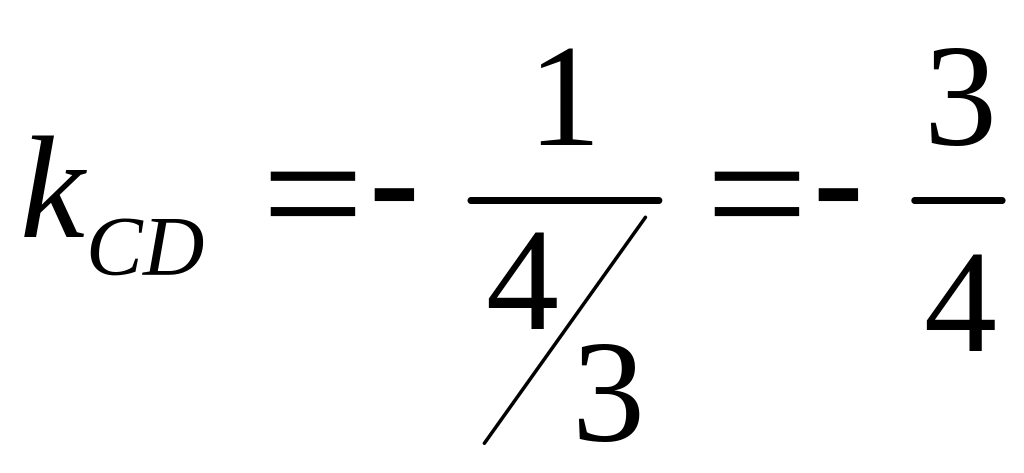Рис. 7. Схематический рисунок треугольника АВС

У прямой СD известен угловой коэффициент и точка С(3; 1). Поэтому можно воспользоваться уравнением прямой (14)

у – у₁ = k(х – х₁).

Учитывая, что х₁ = 3, y₁ = 1 и , получаем уравнение высоты CD:

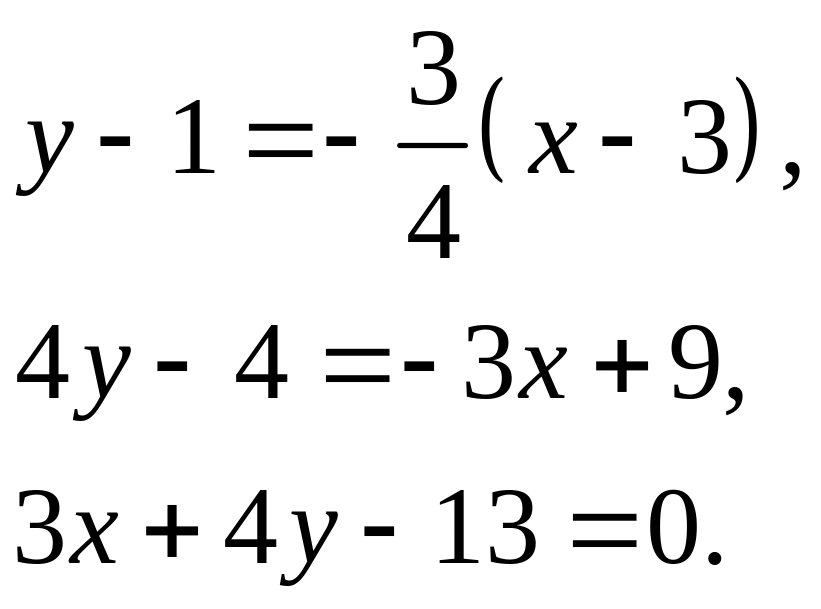
2) Для определения внутреннего угла А воспользуемся формулой (19). Для выбора k₁ и k₂ пригодится рисунок треугольника АВС (см. рис. 7). Так как угол А должен отсчитываться в положительном направлении от прямой АС, то принимаем за k₁ = k_AC, а за k₂ = k_AB. У нас , а k_AC найдём по формуле (18):

.

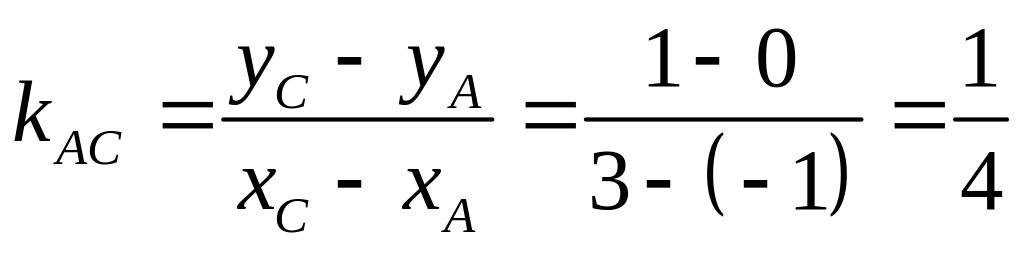Следовательно, . Поэтому внутренний угол А найдём из формулы

,

.

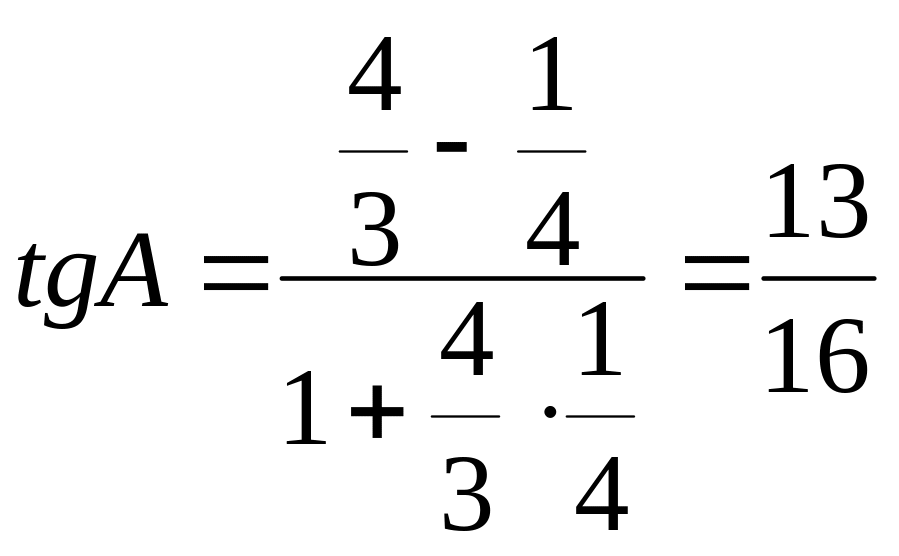3) Длину высоты СD можно рассматривать как расстояние от точки С(3; 1) до прямой АВ. Составим уравнение АВ, как уравнение прямой, проходящей через точку А(–1; 0) с угловым коэффициентом

.

По формуле (14) получаем

.

Остаётся воспользоваться формулой (20).

В результате получаем

.

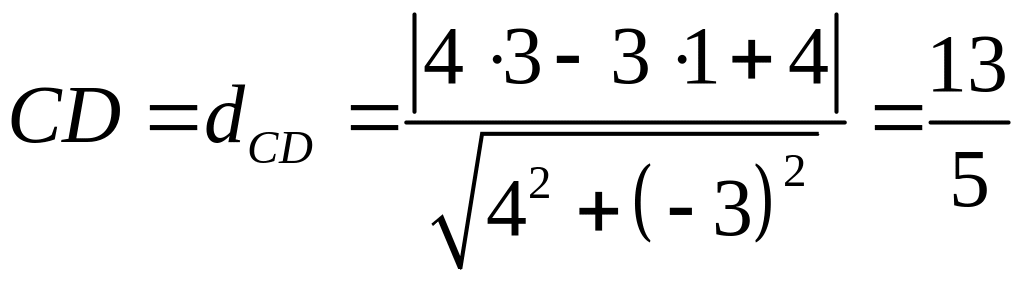Таким образом:

1) — уравнение высоты СD;

2) ;

3) .

3.6. Кривые второго порядка

Кривой (линией) второго порядка называют линию, уравнение которой в прямоугольной системе координат х0у является уравнением второго порядка, т.е. уравнением вида

, (21)

где хотя бы одно из чисел А, В, С отлично от нуля, что обеспечивается условием

А² + В² + С² ≠ 0.

С помощью преобразований системы координат [2, гл. III, § 11] уравнение (21) можно привести к одному из пяти простейших видов (табл. 4).

Таблица 4

Простейшие уравнения кривых 2-го порядка

Уравнение линии	Название	Изображение линии
1	2	3
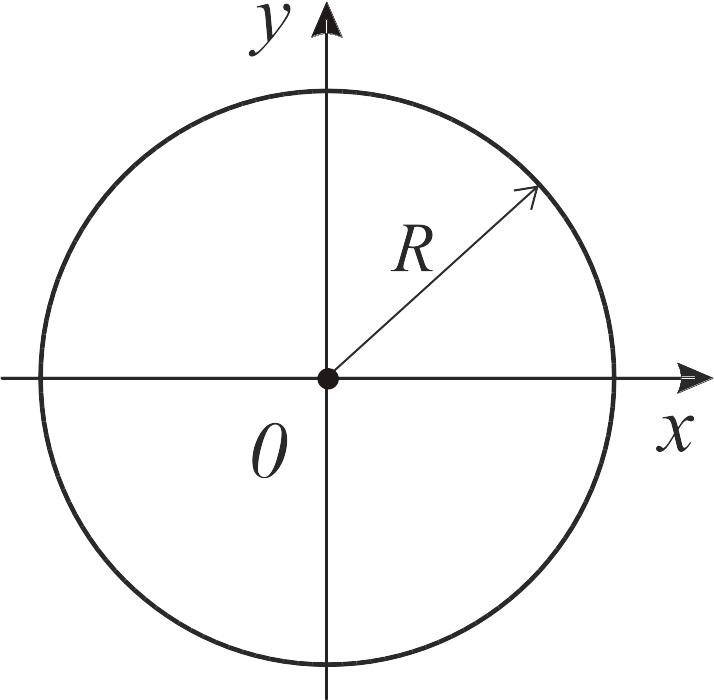
1.	Окружность 0 — центр, R — радиус
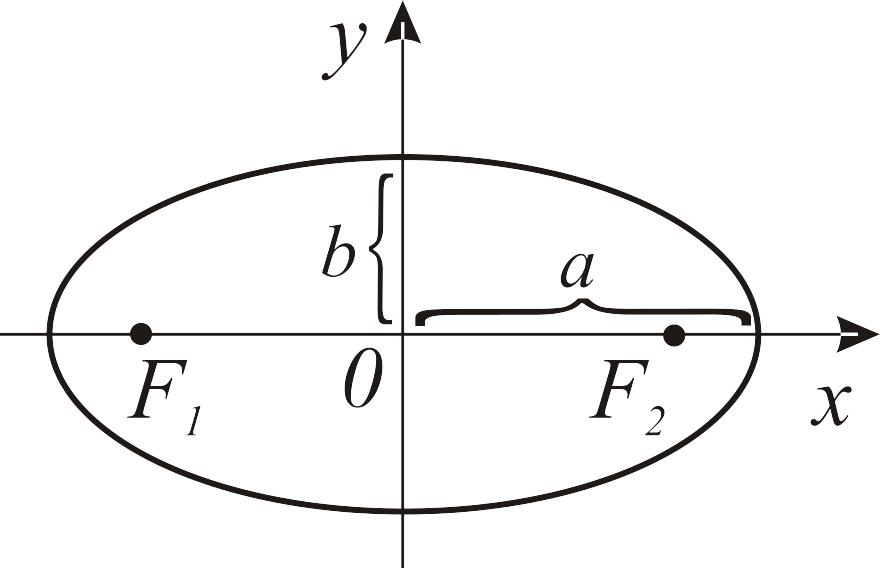
2.	Эллипс 0 — центр, а, в — полуоси	При а > в: F1(–с; о), F2 (с; о) — фокусы, с2 = а2 – в2

Продолжение таблицы 4

1	2	3
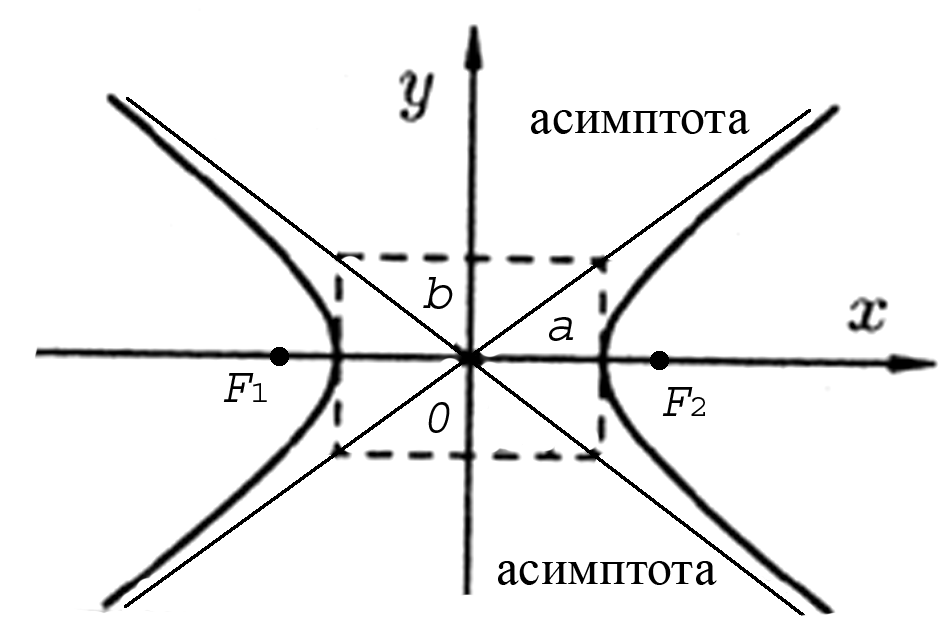
3.	Гипербола 0 — центр, а, в — полуоси	F1(–с; о), F2(с; о) — фокусы, с2 = а2 + в2, x — асимптоты
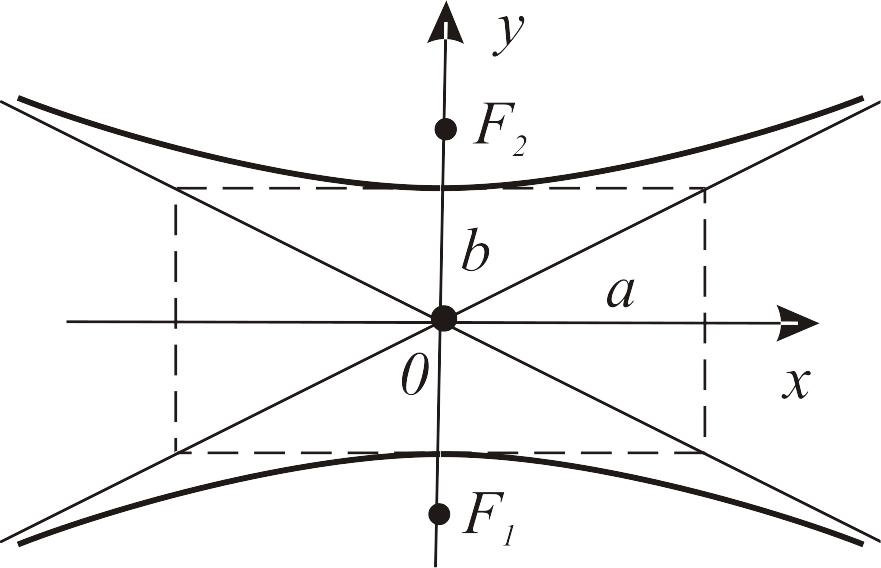
3.1.	Гипербола, сопряженная гиперболе из п. 3	F1(о; –с), F2(о; с) — фокусы, с2 = в2+а2, x — асимптоты
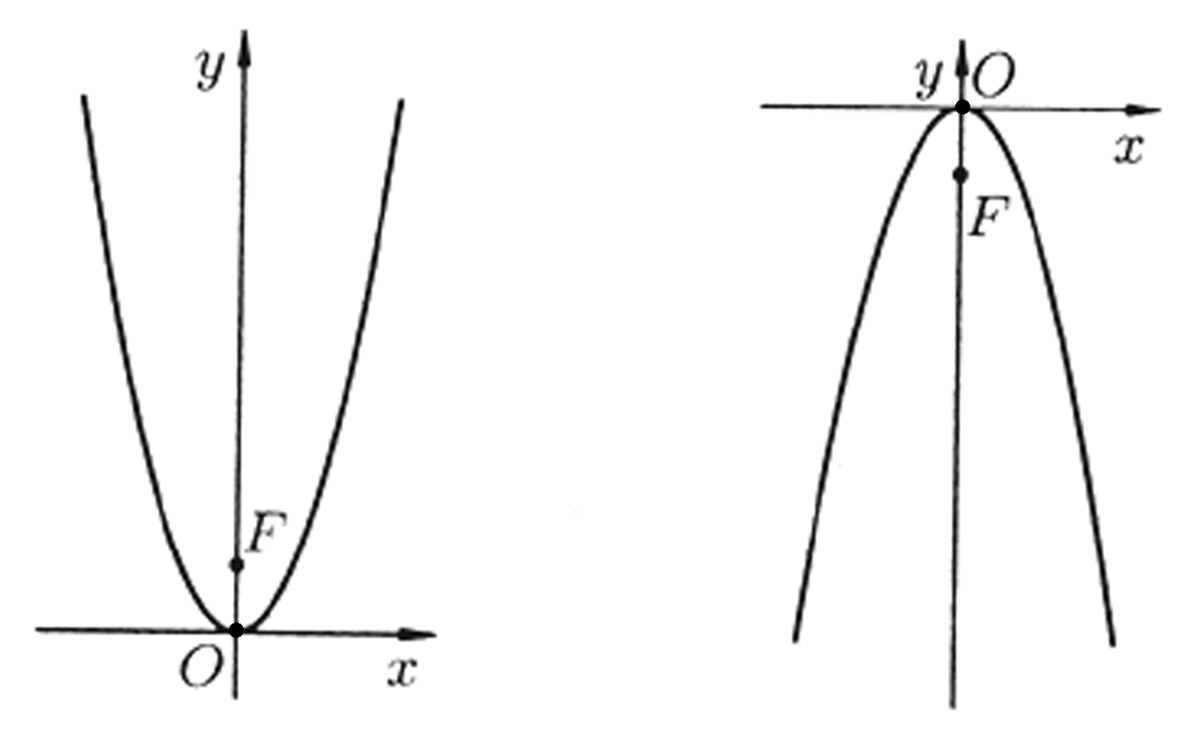
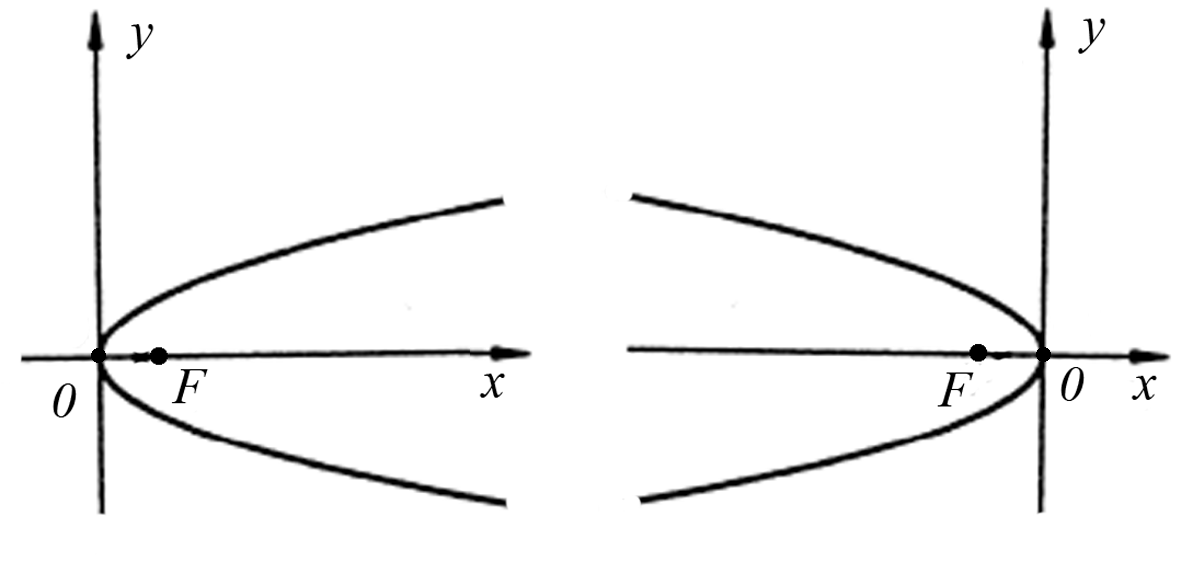
4.	Парабола 0 — вершина, — фокус, — директриса, 0у — ось симметрии	при р > 0 при р < 0
4.1.	Парабола 0 — вершина, — фокус, — директриса, 0х — ось симметрии	при р > 0 при р < 0

Окончание таблицы 4

1	2	3
5.1.	Случаи вырождения	Точка О(0; 0)
5.2.		Мнимая окружность
5.3.		Мнимый эллипс
5.4.		Пара параллельных прямых
5.5.		Пара пересекающихся прямых

Замечание. Если в любом из этих уравнений заменить х и у соответственно на х – х₀ и у – у₀, то полученное при этом уравнение будет определять ту же линию, но сдвинутую параллельно в направлении оси 0х на х₀, а в направлении оси 0у — на у₀. Например, в соответствии со сказанным, уравнение

(22)

будет определять окружность радиуса R с центром в точке О₀(х₀; у₀). Аналогично получаются уравнения эллипса, гиперболы со смещенным центром и параболы со смещенной вершиной.