Оглавление

Оглавление 3

Введение 4

1. Элементы линейной алгебры 5

1.1. Понятие матрицы. Действия над матрицами 5

1.2. Понятие определителя 7

1.3. Решение систем линейных уравнений 9

2. Элементы векторной алгебры 13

2.1. Понятие вектора, виды векторов 13

2.2. Действия над векторами 15

2.3. Применения векторов 18

3. Аналитическая геометрия 22

3.1. Системы координат 22

3.2. Простейшие задачи на метод координат 23

3.3. Понятие уравнения линии на плоскости 24

3.4. Уравнения прямой линии на плоскости 27

3.5. Задачи на прямую на плоскости 29

3.6. Кривые второго порядка 32

3.7. Примеры на построение линий по их уравнениям 34

3.8. Понятие уравнения поверхности в пространстве 37

3.9. Плоскость 39

3.10. Цилиндрические поверхности 40

3.11. Поверхности второго порядка 41

3.12. Уравнения линии в пространстве 42

СПИСОК РЕКОМЕНДУЕМЫХ ИСТОЧНИКОВ 45

Введение

Исторически первым разделом линейной алгебры была теория линейных алгебраических уравнений. В связи с решением систем линейных уравнений, возникли понятия определителя и матрицы.

В 1750 году было получено правило Крамера для решения систем линейных уравнений, а в 1849 году — метод Гаусса. Этот метод является простейшим по числу применяемых операций и может использоваться для приближенного решения систем уравнений, коэффициенты которых также вычислены приблизительно. В 1877 году были получены условия совместности и определенности системы линейных уравнений в терминах коэффициентов самой системы.

Векторная алгебра — один из разделов математики, в котором изучаются линейные операции (сложение, вычитание и умножение на число), а также различные произведения (скалярное, векторное, смешанное) свободных векторов.

Аналитическая геометрия — раздел математики, в котором изучают геометрические объекты (точки, линии, поверхности, тела и т.д.) и их свойства средствами алгебры и математического анализа с помощью метода координат. Сущность метода координат состоит в том, что геометрическим объектам сопоставляются уравнения или их системы, так что геометрические свойства фигур выражаются в свойствах их уравнений. Благодаря этому аналитическая геометрия объединила геометрию с алгеброй и математическим анализом, что плодотворно сказалось на развитии этих трех разделов математики.

Задачи для контрольной работы следует взять из источника [1]. Основные теоретические сведения из учебника [2].

1. Элементы линейной алгебры

В этом разделе следует обратить внимание на определение матрицы, действия над матрицами, вычисление определителей любых порядков и решение систем линейных уравнений. При этом надо уяснить разницу между матрицами и определителями: матрица — это таблица, а определитель — число, которое находят по специальному правилу.

1.1. Понятие матрицы. Действия над матрицами

Определение 1. Матрицей (прямоугольной матрицей) размера m  n называют прямоугольную таблицу из m  n чисел или функций, называемых элементами матрицы.

Матрицу записывают в виде .

Элементы, расположенные на одной горизонтали, образуют строку, а на одной вертикали — столбец матрицы.

Если m = n, то матрицу называют квадратной матрицей n-го порядка.

Например, — квадратная матрица 2-го порядка,

— квадратная матрица 3-го порядка и т.д.

Матрицы можно складывать, вычитать, умножать на число, перемножать. В результате таких действий должна получаться матрица. Первые три операции обычно не вызывают затруднений. Так, чтобы сложить (вычесть) две матрицы одинакового размера, надо сложить (вычесть) соответствующие элементы матриц [2, гл. 1, § 1]; чтобы умножить матрицу любого размера на число, надо умножить на это число все элементы матрицы.

Пример 1. Для матриц найти матрицы:

1) 2А; 2) А + В; 3) 2А – В.

Решение

1)

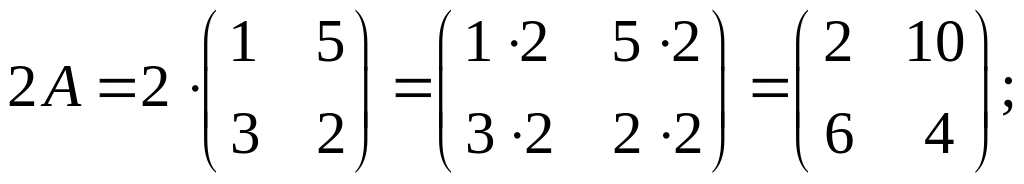
2)

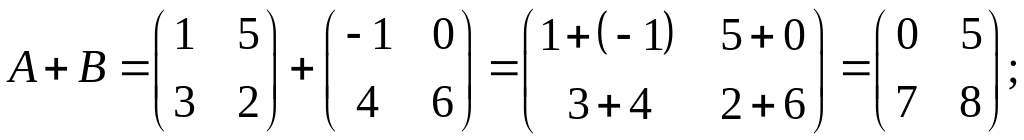
3)

Сложнее с операцией умножения матриц. Рассмотрим эту операцию на примере квадратных матриц 3-го порядка:

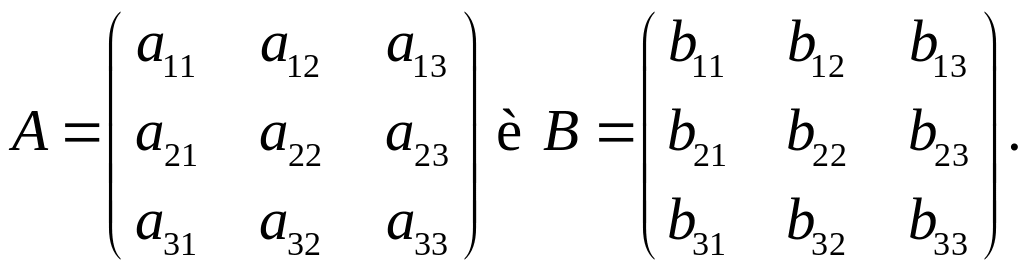
Определение 2. Произведением матрицы А на матрицу В называют новую матрицу 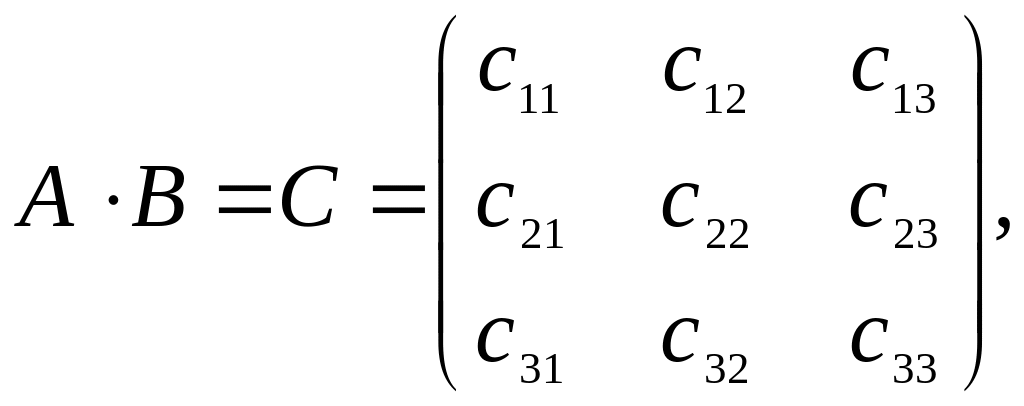элементы которой получаются по правилу

c_ik = a_i1b_1k + a_i2b_2k + a_i3b_3k, (1)

где i, k  {1, 2, 3}.

Таким образом, для получения элемента c_ik матрицы С надо взять сумму произведений элементов i-й строки первой матрицы А и соответствующих элементов k-го столбца второй матрицы В.

Пример 2. Найти произведение матриц

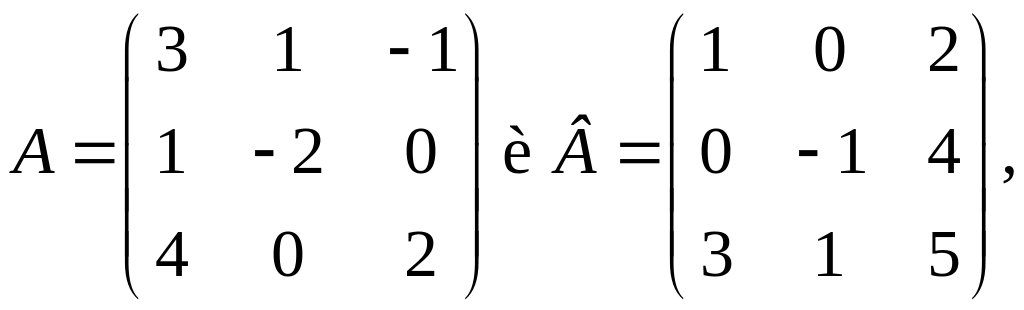
Решение

По определению 2 и формуле (1) находим:

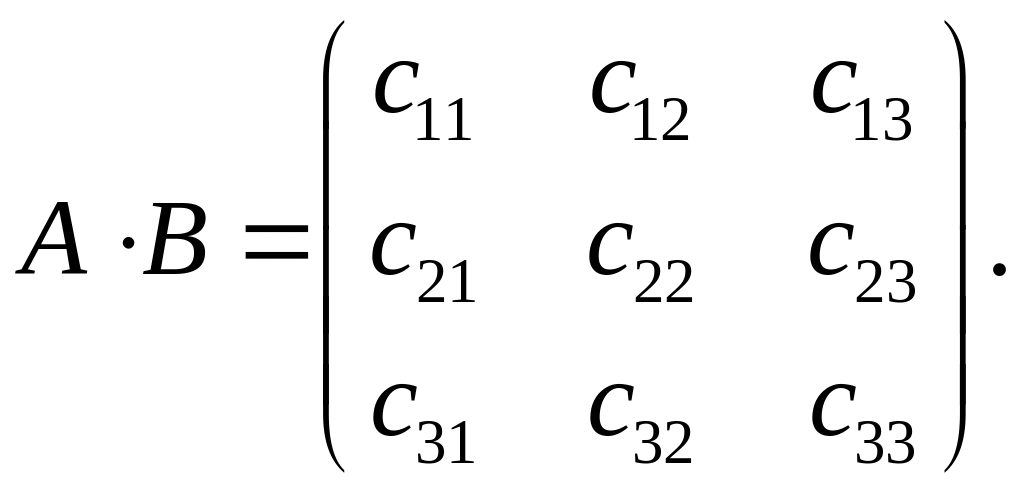
Для получения с₁₁ надо взять из первой матрицы первую строку, а из второй — первый столбец, перемножить соответствующие элементы и сложить:

с₁₁ = 3 · 1 + 1 · 0 + (–1) · 3 = 0.

Аналогично получим остальные элементы матрицы С:

с₁₂ = 3 · 0 + 1 · (–1) + (–1) · 1 = –2; с₁₃ = 3 · 2 + 1 · 4 + (–1) · 5 = 5;

с₂₁ = 1 · 1 + (–2) · 0 + 0 · 3 = 1; с₂₂ = 1 · 0 + (–2) · (–1) + 0 · 1 = 2;

с₂₃ = 1 · 2 + (–2) · 4 + 0 · 5 = –6; с₃₁ = 4 · 1 + 0 · 0 + 2 · 3 = 10;

с₃₂ = 4 · 0 + 0 · (–1) + 2 · 1 = 2; с₃₃ = 4 · 2 + 0 · 4 + 2 · 5 = 18.

Следовательно,

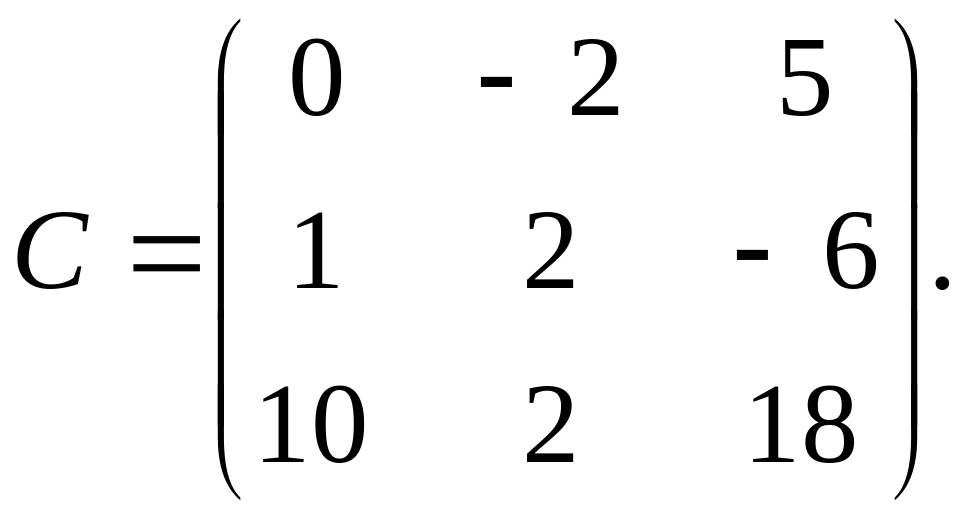
На практике эту операцию лучше выполнять следующим образом:

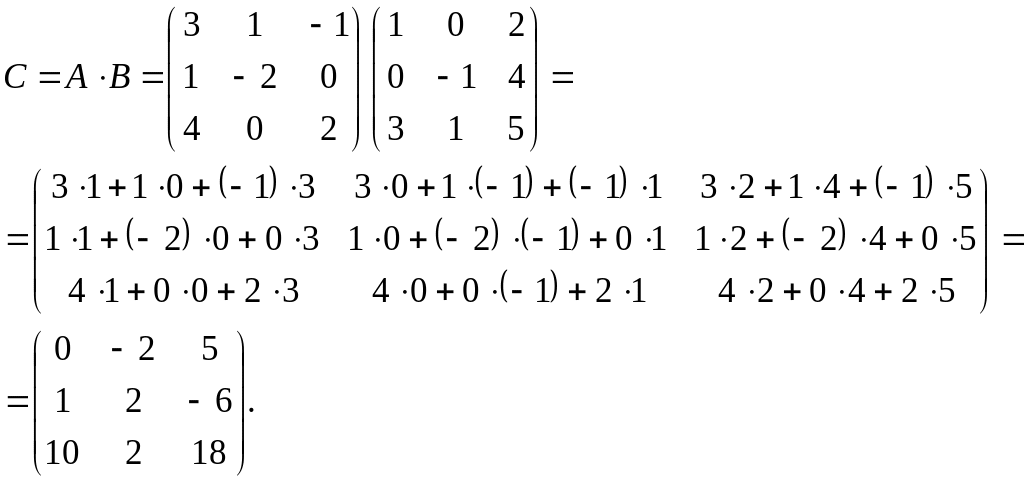
Замечание. Аналогично можно перемножать матрицы любых размеров, но при одном условии: число столбцов первой матрицы должно быть равно числу строк второй матрицы.