Правила округления и записи результатов измерений.

Эмпирически были установлены следующие правила округления рассчитанного значения погрешности и полученного результата измерения.

1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной – если первая цифра равна 3 или более. Пример: 0,00012; 0,0004.

2. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности. Пример: результат 1,072000, погрешность ±0,0001. Результат округляют до 1,0720.

3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Пример: 4567,343 округляют до 4567,34.

4. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу. Пример: 6783,6 округляют до 6784; 12,34501 до 12,35.

5. Если отбрасываемая цифра равна 5, а следующие за ней нули, то последнюю сохраняемую цифру не изменяют, если она четная, и увеличивают на единицу, если она нечетная. Пример: 1234,50 округляют до 1234; 8765,50 – до 8766.

6. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками. Пример: результат 1,072000, погрешность ±0,0001. Вычисления производят с 1,07200.

Лекция №4 Случайные погрешности. Вероятностное описание случайных погрешностей

Присутствие случайных погрешностей в результатах измерений легко обнаруживается из-за их разброса относительно некоторого значения.

Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения.

Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина х_i; в i-м опыте принимает значение, меньшее х:

F(x)=P{x_i<x}=P{- <x_i≤x}

График интегральной функции распределения показан на рис. 1. Она имеет следующие свойства:

• неотрицательная, т.е. F(x) ≥0;

• неубывающая, т.е. F(x₂)≥ F(x₁), если х₂ ≥х₁;

• диапазон ее изменения простирается от 0 до 1, т.е. F(- ) = 0; F(+ ) = 1;

• вероятность нахождения случайной величины х в диапазоне от x₁ до х₂ Р{х₁< х < х₂} = F(x₂) - F(x₁).

Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей р(х)=dF(x)/dx. Она всегда неотрицательна и подчиняется условию нормирования в виде:

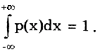
Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х₁; х₂)

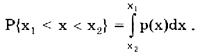
Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [- ; + ] равна единице, т.е. представляет собой достоверное событие. Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (x₁;х₂) равна площади, заключенной под кривой р(х) между абсциссами х₁ и х₂ (рис. 1).

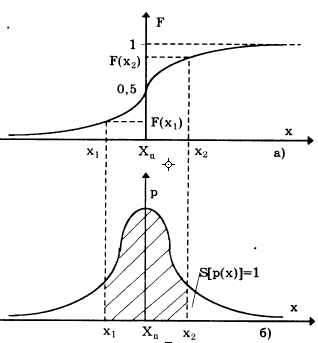
Рис. 1.

Поэтому по форме кривой плотности вероятности p(x) можно судить о том, какие значения случайной величины х наиболее вероятны, а какие наименее.