
- •Лекция №1 Предмет и задачи метрологии.
- •Физические свойства и величины.
- •Системы физических величин и их единиц.
- •Основные и дополнительные единицы физических величин системы си
- •Производные единицы системы си
- •Воспроизведение единиц физических величин и передача их размеров.
- •Лекция №2 Сущность и основные характеристики измерений.
- •Качество измерений.
- •Классификация измерений
- •Методы измерений
- •Лекция №3 Основные понятия теории погрешностей. Классификация погрешностей.
- •Правила округления и записи результатов измерений.
- •Лекция №4 Случайные погрешности. Вероятностное описание случайных погрешностей
- •Числовые параметры законов распределения
- •Основные законы распределения
- •Лекция №5
- •Точечные оценки законов распределения
- •Доверительная вероятность и доверительный интервал
- •Лекция №6 Систематические погрешности и их классификация
- •Способы обнаружения и устранения систематических погрешностей
- •Обработка результатов измерений.
- •Многократные прямые равноточные измерения.
- •Неравноточные измерения.
- •Однократные измерения.
- •Косвенные измерения.
- •Понятие о средстве измерений.
- •Основы теории суммирования погрешностей.
Косвенные измерения.
Косвенные измерения предполагают наличие функциональной связи:
![]() ,
,
где
![]() - подлежащие прямым измерениям аргументы
функции
- подлежащие прямым измерениям аргументы
функции
![]() .
.
Очевидно, что погрешность в оценке зависит от погрешностей при измерениях аргументов.
Косвенные измерения при линейной зависимости между аргументами.
В этом случае:
![]() ;
;
где
![]() - постоянные коэффициенты.
- постоянные коэффициенты.
Предполагается, что корреляция между погрешностями измерений отсутствует. Результат измерения вычисляют по формуле:
![]() ;
;
где
![]() - результат измерения
с введенными поправками.
- результат измерения
с введенными поправками.
Оценку с.к.о. результата измерений вычисляют по формуле:
![]() ,
,
где
![]() - оценка с.к.о. результата измерений
.
- оценка с.к.о. результата измерений
.
Доверительные
границы
![]() случайной погрешности
случайной погрешности
![]() при нормальном распределении погрешностей
вычисляют по формуле:
при нормальном распределении погрешностей
вычисляют по формуле:
![]() ,
,
где
![]() - коэффициент Стьюдента, соответствующей
доверительной вероятности Р и эффективному
числу наблюдений – m.
- коэффициент Стьюдента, соответствующей
доверительной вероятности Р и эффективному
числу наблюдений – m.
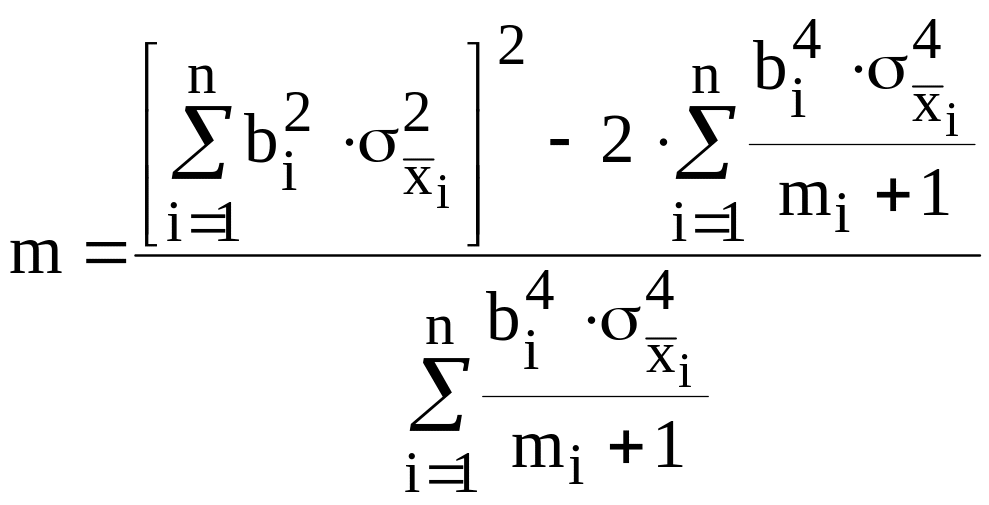 ,
,
где
![]() - число наблюдений при измерении
.
- число наблюдений при измерении
.
При наличии корреляционной связи между аргументами с.к.о. результата косвенного измерения, с.к.о. рассчитывают по формуле:
![]() .
.
Здесь
![]() - несмещенная оценка корреляции между
погрешностями аргументов
- несмещенная оценка корреляции между
погрешностями аргументов
![]() и
и
![]() :
:
![]() ,
,
где
![]() - i-е результаты прямых
измерений k-го и l-го
аргументов, m – число
прямых измерений аргументов.
- i-е результаты прямых
измерений k-го и l-го
аргументов, m – число
прямых измерений аргументов.
Корреляция между аргументами чаще всего возникает в тех случаях, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий (температуры, влажности, напряжению питающей сети, помех и т. п.).
Косвенные измерения при нелинейной зависимости.
При некоррелированных погрешностях измерений используется метод линеаризации путем разложения функции в ряд Тейлора:
![]() ,
,
где
![]() - отклонение отдельного результата
наблюдения
от
;
- отклонение отдельного результата
наблюдения
от
;
![]() - остаточный член разложения.
- остаточный член разложения.
Остаточным членом пренебрегают, если:
![]() ,
,
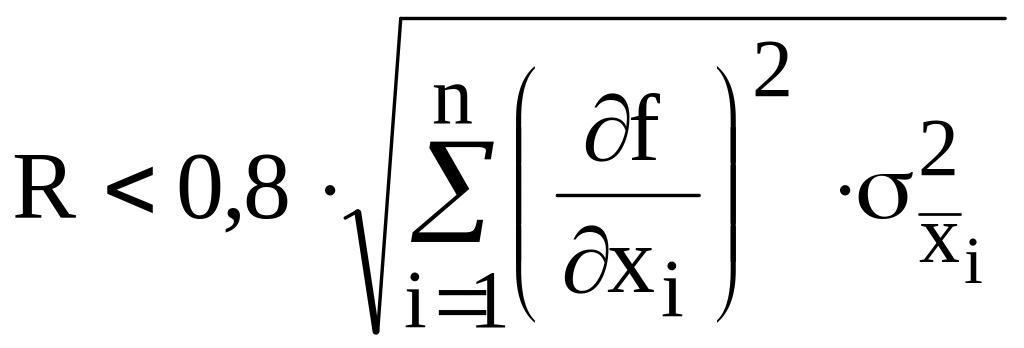 ,
,
где
![]() - оценка с.к.о. случайной погрешности
результата измерения
.
- оценка с.к.о. случайной погрешности
результата измерения
.
Результат измерения вычисляют по формуле:
![]() .
.
Оценку с.к.о. случайной составляющей погрешности результата такого косвенного измерения вычисляют по формуле:
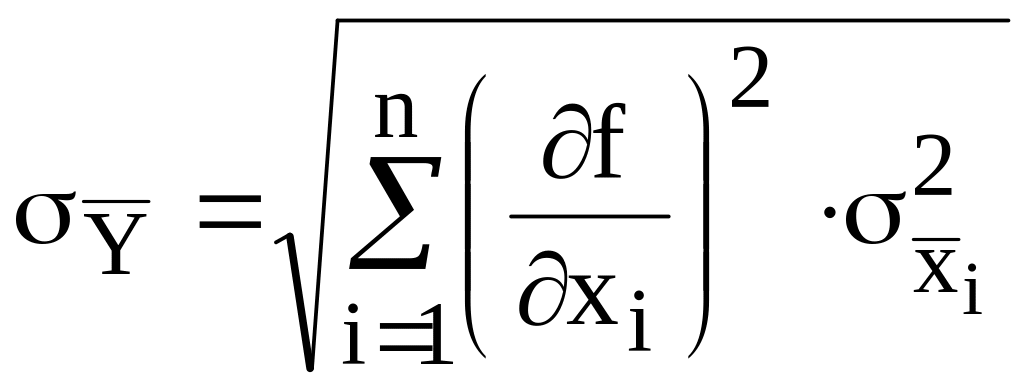 .
.
Доверительные границы:
.
Абсолютная погрешность косвенного измерения равна:
![]() .
.
Пример.
Получить выражение для расчета абсолютной погрешности плотности твердого тела.
![]() - формула для
определения плотности.
- формула для
определения плотности.
Здесь
![]() - масса и объём твердого тела.
- масса и объём твердого тела.
![]() - оценки массы и
объёма, полученные в результате опыта.
- оценки массы и
объёма, полученные в результате опыта.
Разложим
в ряд Тейлора это выражение в окрестности
точки
![]() :
:
![]() .
.
Пренебрегая остаточным членом и учитывая, что
![]() ;
;
![]() ,
,
получим:
![]() .
.
Лекция № 10
Закон распределения суммы двух случайных величин. Композиция законов распределения.
Имеется система двух случайных величин (X,Y) с плотностью распределения f(x,y). Рассмотрим сумму случайных величин X и Y:
![]() ,
,
и найдём закон распределения величины Z.
![]() ,
,
![]() ,
(1)
,
(1)
здесь D – область, для которой с.в. Z<z.

Дифференцируя выражение по z, получим плотность распределения суммы двух случайных величин:
![]() .
(2)
.
(2)
Из соображений симметричности задачи относительно X и Y, можно записать другой вариант этой же формулы:
![]() .
(3)
.
(3)
Особое практическое значение имеет случай, когда случайные величины (X,Y) независимы. Тогда говорят о композиции законов распределения.
Для независимых с.в.:
![]() ,
(4)
,
(4)
и формулы (2) и (3) принимают вид:
![]() ,
(5)
,
(5)
![]() .
(6)
.
(6)
Композицию законов распределения обозначают:
![]() ,
,
![]() - символ композиции.
- символ композиции.
Формулы
(5) и (6) удобны, когда законы распределения
(или по крайней мере, один из них) заданы
одной формулой на всем диапазоне значений
аргументов (от -![]() до
до
![]() ).
В противном случае, удобнее пользоваться
непосредственно функцией распределения
).
В противном случае, удобнее пользоваться
непосредственно функцией распределения
![]() и продифференцировать эту функцию (т.е.
вычислить G(z)).
и продифференцировать эту функцию (т.е.
вычислить G(z)).
Пример.
Составить композицию двух законов равномерной плотности, заданных на одном и том же участке (0,1):
![]() при 0<x<1;
при 0<x<1;
![]() при 0<y<1.
при 0<y<1.
Решение.

Найдем функцию распределения G(z) с. в. Z=X+Y.
Рассмотрим случайную точку (x,y) на плоскости x0y. Область её возможных положений – квадрат R со стороной, равной 1 (рис. 1).


Имеем:
![]()
где область D – часть квадрата R, лежащая левее и ниже прямой z=x+y.
Очевидно,
![]() ,
,
где SD – площадь области D.
Составим выражение для площади области D при различных значениях z, пользуясь рис.1 и рис.2.
при z<0 G(z)=0;
при 0<z<1
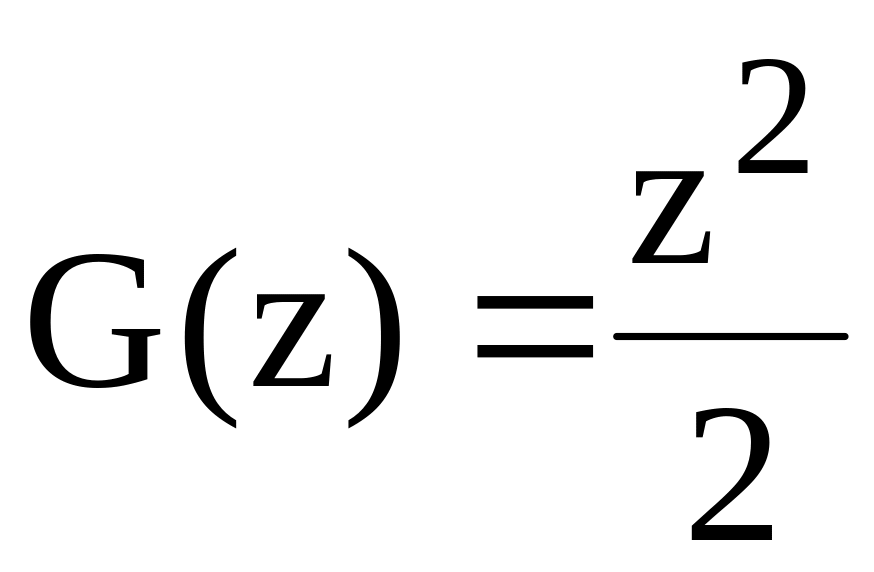 ;
;при 1<z<2
 ;
;при z>2 G(z)=1.
Дифференцируя эти выражения, получим:
при z<0 g(z)=0;
при 0<z<1 g(z)=z;
при 1<z<2 g(z)=2-z;
при z>2 g(z)=0.
Такой закон носит название «закона Симпсона» или закона треугольника.

Для трех случайных величин, распределенных по равномерному закону, получим график закона плотности распределения, состоящий из трех отрезков- парабол.

При 6 и более случайных величинах – закон распределения будет практически «нормальным», т. е. иметь нормальное распределение.
Об условиях возникновения нормального распределения и о причинах его широкой распространенности в случайных явлениях природы. Оно возникает в тех случаях, когда складывается много независимых (или слабо зависимых) случайных величин x1, x2,…,xn
![]() ,
,
(причем эти величины сравнимы по порядку своего влияния на рассеивание суммы).
Тогда, каковы бы ни были законы распределения отдельных величин x1, x2,…,xn, закон распределения их суммы X будет близок к нормальному (причем тем ближе, чем больше число слагаемых n).
Это и есть содержание центральной предельной теоремы теории вероятностей.
Лекция № 11
Средства измерений.
