18

Лабораторная работа № 2 «Численное интегрирование»

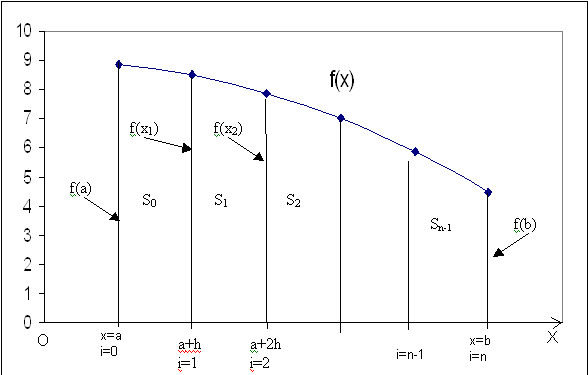
В рамках этой лабораторной работы необходимо вычислить значение определенного интеграла 3-мя методами: прямоугольников, трапеций и Симпсона. Методы численного интегрирования применяются тогда, когда невозможно или очень сложно найти первообразную для подынтегральной функции. Сущность численного интегрирования заключается в замене значения интеграла на значение площадиSкриволинейной фигуры, ограниченной осью абсциссOX, кривойf(x) и прямойx=aи прямойx=b.

Для вычисления этой площади надо отрезок [a,b] разделить наnравных частей. Числоnдолжно бытьчетным. Пронумеровать точки деления от «0» доn, так чтобы первая точка х=а имела номер 0, а последняя- х=b- номерn. Расстояние между соседними точкамиh=x_i+1-x_iможно вычислить по формуле, а значение.

Площадь криволинейной фигуры S можно представить как сумму площадей элементарных фигурS_i.

В свою очередь площадь каждой элементарной криволинейной фигуры будем моделировать площадями фигур, который легко вычислить: прямоугольником, трапецией и фигурой, ограниченной параболой.

Метод прямоугольников

Одна сторона каждого прямоугольника равна h , а другая - f(xi), тогда

Обратите внимание на то, что суммируется n-1площадей прямоугольников.

S₀

h

h

Метод трапеций.

Площадь элементарной фигуры моделируется площадью трапеции, у которой высота равна h , а параллельные стороны равны соответственноf(x _i )иf(x _i+1 ), тогда формула метода трапеции будет такова:

После алгебраических преобразований получим окончательный вид формулы трапеции:

Метод Симпсона

Этот метод основан на замене на промежутках [x_i,x_i+1]функцииf(x) на параболу.

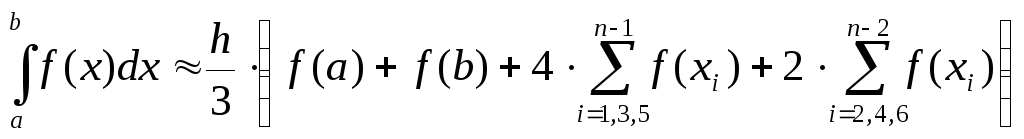
Для этого метода принципиально важно, чтобы nбыло четным, иначе невозможно построить параболы.

Мы будем сравнивать результаты, полученные тремя методами, поэтому число разбиений nдолжно быть одинаковым во всех трех формулах.

Пример.

Пусть надо вычислить . Вообще-то, для такого примера не требуется численного интегрирования. Несложно определить, что значение этого интеграла 2,3333. На этом примере удобно оценить погрешность методов. Пустьn=4,тогдаh=(2-1)/4=0.25

Для вычисления интеграла потребуется таблица значений функции

№ точки	значение xi	f(xi)
0	1.00	1.0000
1	1.25	1.5625
2	1.50	2.2500
3	1.75	3.0625
4	2.00	4.0000

Метод прямоугольников

S ^{прямоуг}=0.25(1.000+1.5625+2.25+3.0625)=1.96875

Метод трапеций

Метод Симпсона

Отметим, что метод Симпсона в данном случае дал точное значение, так как функция х² была промоделирована параболой.

Задание на индивидуальную работу

1. Построить график подынтегральной функции

2. Для n=20 построить таблицу значений функции и вычислить определенный интеграл 3-мя методами. Расхождение между значениями, полученными разными методами не должно превышать 0.5.

3. В стандартном модуле (Сервис – Макрос – Редактор VBA,Insert–Module) создать пользовательские функции для всех трех методов. Входными аргументами должны быть пределы интегрирования а иbи число разбиений отрезкаn.

Ниже приведен пример формирования рабочего листа в Excelдляn=20

Тексты пользовательских функций

Функция Spriam(a, b, n) для вычисления определенного интеграла методом прямоугольников.

Function Spriam(a, b, n)

Dim x, S, y, h As Double

Dim i As Integer

If b < a Then

MsgBox "Проверьте диапазон [a,b]"

Exit Function

End If

h = (b - a) / n

S = 0

For i = 0 To n - 1

x = a + i * h

y = x ^ 2

S = S + y

Next i

Spriam = S * h

End Function

Функция Strap(a, b, n) для вычисления определенного интеграла методом трапеций.

Function Strap(a, b, n)

Dim x, S, y, h As Double

Dim i As Integer

If b < a Then

MsgBox "Проверьте диапазон [a,b]"

Exit Function

End If

h = (b - a) / n

S = 0

For i = 1 To n - 1

x = a + i * h

y = x ^ 2

S = S + y

Next i

S = 2 * S + a ^ 2 + b ^ 2

Strap = S * h / 2

End Function

Функция Scimp(a, b, n) для вычисления определенного интеграла методом Симпсона.

Function Scimp(a, b, n)

Dim x, S, y, h As Double

Dim i As Integer

If b < a Then

MsgBox "Проверьте диапазон [a,b]"

Exit Function

End If

If n / 2 <> Int(n / 2) Then

MsgBox "должно быть четным"

Exit Function

End If

h = (b - a) / n

S = 0

For i = 1 To n - 1 Step 2

'If i / 2 <> Int(i / 2) Then

x = a + i * h

y = x ^ 2

S = 4 * y + S

'End If

Next i

For i = 2 To n - 2

If i / 2 = Int(i / 2) Then

x = a + i * h

y = x ^ 2

S = 2 * y + S

End If

Next i

S = S + a ^ 2 + b ^ 2

Scimp = S * h / 3

End Function

Методические указания по выполнению лабораторной работы

«Решение нелинейных уравнений»

Оглавление

Тексты пользовательских функций 5

Общие положения 7

1 этап. 7

2 этап. 9

Метод половинного деления (дихотомии) 9

Метод хорд 12

Метод Ньютона (касательных). 16

Общие положения

Решением или корнями уравнения Y(x)=0, называются такие значения аргументах, при которых значение функцииY(x) становится равным нулю (равенство обращается в верное тождество). Только 2 класса уравнений – линейноеax + b = 0и квадратноеax² + bx + c = 0 – имеют в общем случае аналитическое решение в виде формул. Все остальные классы уравнений имеют аналитические решения только в некоторых частных случаях.

В данной лабораторной работе мы познакомимся с численными методами нахождения корней для любых классов уравнений. При этом определять значение корня мы будем с некоторой заданной точностью .

Вычисление корня нелинейного уравнения осуществляется в 2 этапа:

1 этап. Определение промежутков локализации [a,b]. Промежуток локализации [a,b] это такой промежуток обязательно есть корень функции, причем только один. Определение промежутков локализации выполняется с помощью построения таблицы значений и графика функции;

2 этап. Уточнение корней из выбранных промежутков локализации. На этом этапе применяются методы метод половинного деления (дихотомии) ,касательных(Ньютона), хорди другие.

1 Этап.

Промежуток [a,b], на котором следует искать корень функции должен удовлетворять 2 условиям:

- функция Y(x)должна быть непрерывна на этом промежутке [a,b]:

- значения функции Y(x)на концах промежутка в точкахaиbдолжны иметь разные знакиY(a) * Y(b) < 0

Рассмотрим уравнение x³ -5x + 3 = 0. функцияY(x) = x³ -5x + 3 является непрерывной при любомх, так что первое условие выполняется всегда. Для определения промежутков, где функция меняет знак, построим таблицу значений функции. См. рисунок 1.

X	Y(x)=x3-5x +3
-3	-9
-2.5	-0.125	первый корень в промежутке [-2.5, -2]
-2	5
-1.5	7.125
-1	7
-0.5	5.375
0	3
0.5	0.625	второй корень в промежутке [0.5, 1] третий корень в промежутке [1, 1.5]
1	-1
1.5	-1.125
2	1

Рис. 1

Поскольку на промежутке от -2.5 до -2 функция Y(x)поменяла знак, (Y(-2.5)=-0.125,Y(-2.0)=5) и функция непрерывна, то где-то на этом промежутке она принимает значение 0, то есть на этом промежутке у функцииY(x) = x³ -5x + 3 есть корень. У кубической функции должно быть 3 корня, что и обнаруживается при дальнейшем анализе таблицы.

На рисунке 2 представлен график этой функции, иллюстрирующий промежутки локализации корней.

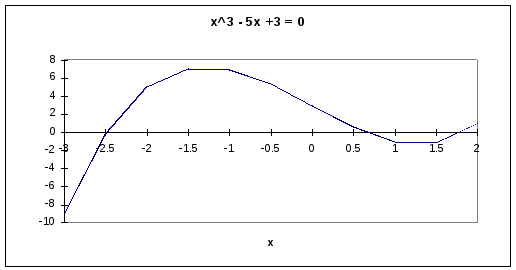
Рис. 2

Рассмотрим другой пример: tg(x) – x + 2 =0, левую часть уравнения обозначимZ(x)= tg(x) – x +2. Как известно,tg(x) имеет разрывы в точкахx=n. Построим таблицу значений функцииZ(x), как показано на рисунке 3.

x	tg(x)-x+2
-2.5	5.247	На промежутке [ -2, -1.5] разрыв функции
-2	6.185
-1.5	-10.601	Корень на промежутке [ -1.5 до -1.0]
-1	1.443
-0.5	1.954
0	2.000
0.5	2.046
1	2.557
1.5	14.601	На промежутке [ 1.5, 2.0] разрыв функции
2	-2.185
2.5	-1.247
3	-1.143

Рис. 3.

Первое изменение знака функции Z(x)мы видим на промежутке [-2.0, -1.5], однако в точкеx= -/2 = -1.5759 имеется разрыв функции, нарушено условие непрерывности, поэтомуна промежутке [-2.0, -1.5] корня нет. На промежутке [-1.5, -1.0] опять изменился знак функции, при чем на этом промежутке функцияZ(x) непрерывна, поэтому промежуток [-1.5, -1.0] является промежутком локализации и содержит корень функции. Дальнейший анализ таблицы значений показывает, что на промежутке [1.5, 2.0] снова происходит смена знака функции, но в точкеx=/2 = 1.5759 имеется разрыв функции, следовательно корня на этом промежутке нет.

Рисунок 4 показывает график функции Z(x)= tg(x) – x +2. На рисунке видно, что на промежутках [-2.0, -1.5] и [1.5, 2.0] не может быть корней функцииZ(x).

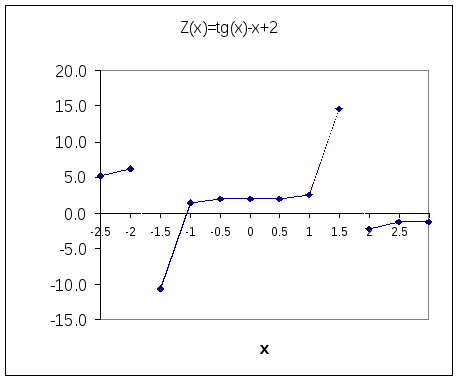
Рис. 4.